最优化简介-第三节：最优化基本概念

Posted 2022-10-28 快乐江湖

文章目录

• 一：最优化研究基本过程
• 二：全局最优解和局部最优解
• 三：优化算法
• • （1）迭代算法
  • （2）收敛问题
  • （3）算法的渐进收敛速度
  • （4）算法复杂度

一：最优化研究基本过程

最优化研究基本过程：一般来说，最优化算法研究可以分为如下几步

• 构造最优化模型：模型的构造和实际问题相关
• 确定最优化问题的类型：之所以要分类是因为不存在一个统一的算法可以适用于优化问题
• 设计算法
• 实现算法

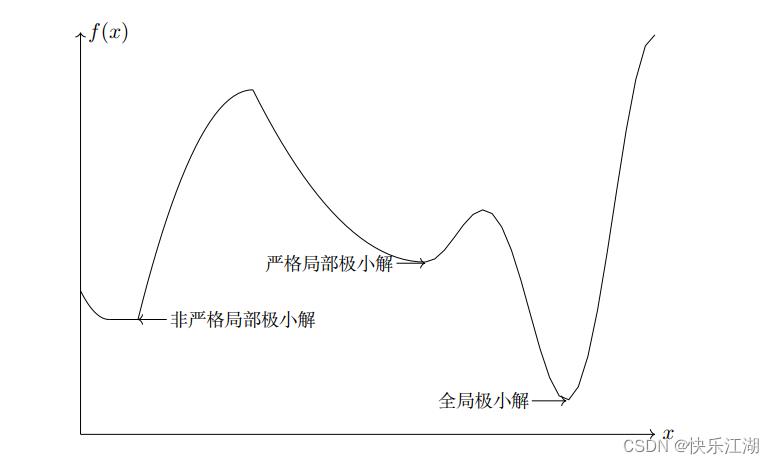
二：全局最优解和局部最优解

定义：对于可行点$\overline{x}(\overline{x}\in \chi )$，定义如下概念

• 若$\forall x\in \chi$，都有$f(\overline{x})\le f(x)$，那么称$\overline{x}$为全局最优解
• 如果存在$\overline{x}$的一个$\xi$领域$N_{\xi }(\overline{x})$使得$f(\overline{x})\le f(x)$，那么称$\overline{x}$为局部最优解；进一步如果有$f(\overline{x})<f(x)$且$x\ne \overline{x}$成立，则称$\overline{x}$为严格局部最优解

三：优化算法

（1）迭代算法

迭代算法：由于实际问题的复杂性，所以我们在求解时往往只能够得到其局部最优解，而不能得到全局最优解，所以我们常常会使用迭代算法。其基本思想为：从一个初始点$x^0$出发，按照某种给定的规则进行迭代，得到一个序列$x^k$

• 如果迭代在有限步内终止，那么最后一个点就是优化问题的解
• 如果迭代点列是无穷集合，那么希望该序列的极限点为优化问题的解

（2）收敛问题

收敛问题：在算法设计中，还需要考虑算法产生的点列是否收敛到优化问题的解。考虑无约束情形，对于一个算法，给定初始点$x^0$，记算法迭代产生的点列为$x^k$

• 如果$x^k$在某种范数的意义下满足$li{m}_{k->\infty }||x^k-x^{\ast }||=0$，且收敛的点$x^{\ast }$为一个局部（全局）极小解，那么我们称该点列收敛到局部（全局）极小解，相应算法称为是依点列收敛到局部（全局）极小解的
• 如果从任意初始点$x^0$出发，算法都是依点列收敛到局部（全局）极小解的。记对应的函数值序列为$f(x^k)$，可以定义算法的（全局）依函数值收敛到局部（全局）极小值概念

注意

• 对于凸优化问题，因为其任何局部最优解都是全局最优解，所以算法的收敛性都是相对于全局极小而言的
• 除了点列和函数值的收敛外，实际中常用的还有每个迭代点的最优性条件的收敛
• 对于带约束的情形，给定初始点$x^0$，算法产生的点列$x^k$不一定是可行的。考虑到约束违反的情形，我们需要保证$x^k$在收敛到$x^{\ast }$的时候，其违反度是可以接受的。除此之外，算法的收敛性定义和无约束情形相同

（3）算法的渐进收敛速度

$Q$-收敛速度：设$x^k$为算法产生的迭代点列且收敛于$x^{\ast }$

• Q-线性收敛： 对充分大的$k$有，$\frac{||x^{k+1}-x^{\ast }||}{||x^k-x^{\ast }||}\le a$，$a\in (0,1)$
• Q-超线性收敛： 对充分大的$k$有，${\lim }_{k->\infty }\frac{||x^{k+1}-x^{\ast }||}{||x^k-x^{\ast }||}=0$
• Q-次线性收敛： 对充分大的$k$有，${\lim }_{k->\infty }\frac{||x^{k+1}-x^{\ast }||}{||x^k-x^{\ast }||}=1$
• Q-二次收敛： 对充分大的$k$有，$\frac{||x^{k+1}-x^{\ast }||}{||x^k-x^{\ast }|{|}^2}\le a$，$a>0$

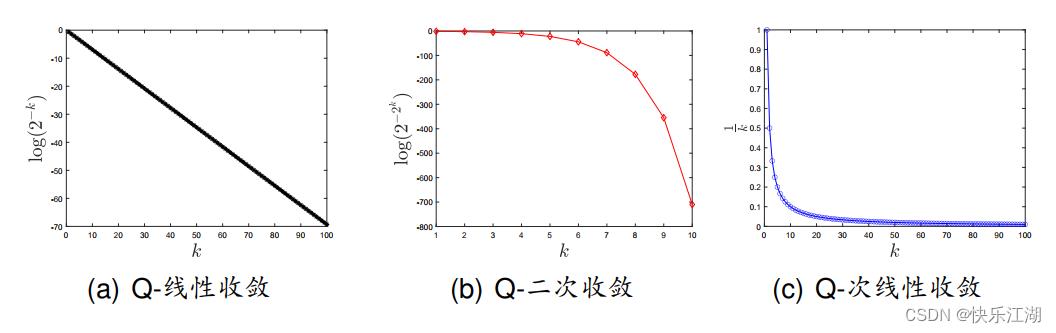
$R$-收敛速度：设$x^k$为算法产生的迭代点列且收敛于$x^{\ast }$，已定义$R$-线性收敛为例，类似可以定义$R-$超线性收敛和$R$