最优化所需基础知识-第三节:重要凸集举例
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化所需基础知识-第三节:重要凸集举例相关的知识,希望对你有一定的参考价值。
文章目录
(1)超平面
超平面:任取非零向量 a ∈ R n a\\in \\R^n a∈Rn,形如
x ∣ a T x = b , a ≠ 0 , b ∈ R \\x|a^T x=b\\,a\\not=0,b\\in R x∣aTx=b,a=0,b∈R
的集合称之为超平面
上述定义还可以表示为:
x ∣ a T ( x − x 0 ) = 0 \\x|a^T (x-x_0)=0\\ x∣aT(x−x0)=0
- x 0 x_0 x0为超平面上任意一点
下图:是由
R
2
R^2
R2中由法向量
a
a
a和超平面上一点
x
0
x_0
x0确定的超平面,对于超平面上任意一点
x
x
x,
x
−
x
0
x-x_0
x−x0都垂直于
a
a
a

(2)半空间
超平面:任取非零向量 a ∈ R n a\\in \\R^n a∈Rn,形如
x ∣ a T x ≤ b \\x|a^Tx \\leq b\\ x∣aTx≤b
的集合称为半空间
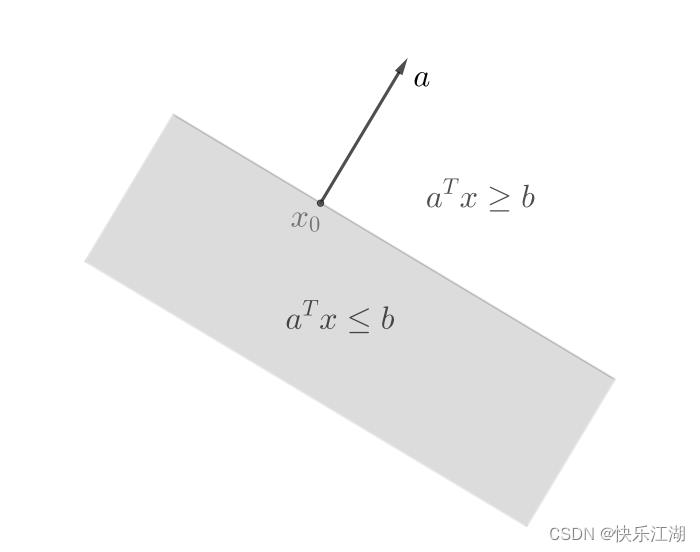
一个超平面会将 R n R^n Rn划分为两个半空间,对于下图中的 R 2 R^2 R2来说
- 由 a T x ≥ b a^Tx \\geq b aTx≥b决定的半空间(白色部分) :是向 a a a扩展的部分
- 由 a T x ≤ b a^Tx \\leq b aTx≤b决定的半空间(阴影部分) :是向 − a -a −a扩展的部分,向量 a a a是这个半空间向外的法向量
(3)超平面和半空间与凸集和仿射集的关系
A:关系
关系:超平面和半空间与凸集和仿射集的关系总结如下
- 超平面是仿射集
- 超平面是凸集
- 半空间不是仿射集
- 半空间是凸集
B:证明(部分)
证明:超平面为凸集
证明:半空间为凸集
(4)(范数)球和椭球
(范数)球:设空间中到某一定点 x c x_c xc(称为球心)的距离小于等于定值 r r r(称为半径)的点的集合为(范数)球,即
B ( x c , r ) = x ∣ ∣ ∣ x − x c ∣ ∣ ≤ r = x c + r u ∣ ∣ ∣ u ∣ ∣ ≤ 1 B(x_c, r)=\\x|\\quad ||x-x_c||\\leq r\\=\\x_c+ru|\\quad ||u||\\leq1\\ B(xc,r)=x∣∣∣x−xc∣∣≤r=xc+ru∣∣∣u∣∣≤1
- 一般来说,我们使用二范数度量距离,即使用2-范数球,即 x ∣ ∣ ∣ x − x c ∣ ∣ ≤ r \\x|\\quad ||x-x_c||\\leq r\\ x∣∣∣x−xc∣∣≤r
椭球:设形如
x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 = x c + A u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 \\x| (x-x_c)^TP^-1(x-x_c)\\leq1\\=\\x_c+Au|\\quad ||u||_2\\leq 1\\ x∣(x−xc)TP−1(x−xc)≤1=xc+Au∣∣∣u∣∣2≤1
的集合为椭球,其中 x c x_c xc称为椭球中心。 P P P对称正定且 A A A可逆
(5)范数锥
范数锥:球和椭球的范围完全取决于 x x x的范围,而锥的范围则同时受 x x x和 t t t的控制。将形如
( x , t ) ∣ ∣ ∣ x ∣ ∣ ≤ t \\(x, t)|\\quad ||x||\\leq t\\ (x,t)∣∣∣x∣∣≤t
的集合为范数锥
- 使用二范数度量距离的锥称为二次锥,也称为冰淇淋锥
(6)多面体
多面体:我们把满足线性等式和不等式组的点的集合称为多面体,即
x ∣ A x ≤ b , C x = d \\x|Ax\\leq b,Cx=d\\ x∣Ax≤b,Cx=d
其中 A ∈ R m × n A\\in \\R^m×n A∈Rm×n, C ∈ R p × n C\\in \\R^p×n C∈Rp×n, x ≤ y x\\leq y x≤y表示向量 x x x的每个分量都 ≤ y \\leq y ≤y的对应分量。多面体是有限个半空间和超平面的交
(7)单纯形
单纯形:单纯性是一类特殊的多面体。在
R
n
\\R^n
Rn空间中选择
v
0
,
v
1
,
.
.
.
,
v
k
\\v_0, v_1, ... ,v_k\\
v0,v1,...,vk共计
k
+
1
k+1
k+1个点,并要求向量线段
v
1
−
v
0
,
v
2
−
v
1
,
.
.
.
,
v
k
−
v
k
−
1
,
v
0
−
v
k
v_1-v_0,v_2-v_1,...,v_k-v_k-1,v_0-v_k
v1−v0,v2−v1,...,vk−vk−1,v0−vk构成线性无关组,则
v
0
,
v
1
,
.
.
.
,
v
k
\\v_0, v_1, ... ,v_k\\