贪心1：从田忌赛马说起

Posted 2022-02-09 纵横千里，捭阖四方

我们知道算法有三座大山：回溯、贪心和动态规划。前面断断续续用了半个多月，将回溯的基本问题过了一遍。从前面的题目可以看到回溯就是递归的进一步拓展。在递归中，回归阶段由系统给我们做好，我们主要收割结果就行了。但是在回溯中，我们要自己负责一部分撤销工作。而所有的回溯问题几乎都是这个套路来的。而回溯类型的题目也有非常明确的特点，层次太深太灵活，暴力枚举做不到，但是可以局部枚举。所以局部枚举就是一个for循环，而层次问题就交给递归来做。因此不管是代码结构还是画出来的结构图，各个题目都非常类似。不同的是去重等一些问题的处理上，虽然仍然不简单，但是有模板就没模板强。

而贪心则与回溯不同，贪心问题没有明确的套路，不仅实现没有，而怎么找到解决方法也更多是我们通过眼睛看出来的，写代码只是将这个过程给实现了一下而已。之所以这样，自然和贪心的特征有关系。

我们知道在春秋战国时期有个田忌赛马的故事。简单来说就是田忌常同齐威王赛马，三局两胜制。三场分别使用是上等、中等、下等三种马来比赛。开始逐级PK的时候，田忌全输了。孙膑给建议，从自己的下等马对阵对方的上等马，先输一局。然后让自己的上等马对阵对方的中等马，赢！最后让自己的中等马对阵对方的下等马，赢！最后三局两胜制，赢了比赛。这就是贪心的经典例子。你能说这个问题有什么模板套路马？没有，很多贪心的问题都要具体情况具体分析。

那到底什么是贪心呢？解释起来还挺绕，贪心的的本质是选择每一阶段的最优，最终得到全局最优。例如有面值为100，50，20，10，5，1数量不限的纸币，让你拿走最大数额的钱。小孩子都知道要先拿面值高的，最后还能扛就拿面值小的。每次拿面额最大的就是局部最优，最后可以拿走最大额就是全局最优。

贪婪算法将问题分为多个阶段，每个阶段都选择当前状态下的最优决策，而不考虑对后续决策的影响，也就是只顾当下的意思。贪心法假设通过局部最优能够找到全局最优。很明显，不是所有问题都具备这种特性的，因此贪心也只是适用某些特定场景的问题。常见的应用场景有：

• 1.排序问题：选择排序、拓扑排序
• 2.优先队列：堆排序
• 3.赫夫曼压缩编码
• 4.图里的Prim、Fruskal和Dijkstra算法
• 5.硬币找零问题
• 6.分数背包问题
• 7.并查集的按大小或者高度合并问题或者排名
• 8.任务调度部分场景
• 9.一些复杂问题的近似算法

贪心问题的解法更多是我们看出来的，如果想证明也非常困难，一般可以使用归纳法或者反证法。但是这个证明可能比让你证明你妈是你妈还困难。好在面试过程中我们更多是看如何写代码，证明就让数学专业的人做就好了。而且贪心的常见题目也是非常有限的，因此我们仍然先认真分析一些常见问题的解决方法，学有余力再继续研究其他问题。

我们先看一个简单的题目，LeetCode455，分发饼干。假设你要给孩子们一些小饼干。但是每个孩子最多只能给一块饼干。

每个孩子的饭量不同，对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。示例：

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

这里既要满足小孩的胃口，也不要造成饼干尺寸的浪费。大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

所以，这里可以使用贪心策略，先将饼干数组和小孩数组排序。 然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量就可以了。也就是这样：

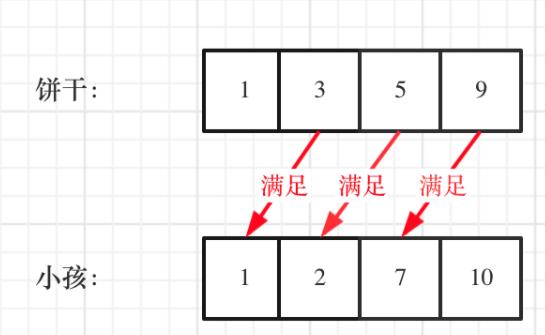
这里我们就考虑胃口，大饼干先喂饱大胃口，最后看能满足几个孩子的需要就行。

   public int findContentChildren(int[] g, int[] s) 
        Arrays.sort(g);
        Arrays.sort(s);
        int count = 0;
        int start = s.length - 1;
        // 遍历胃口
        for (int index = g.length - 1; index >= 0; index--) 
            if(start >= 0 && g[index] <= s[start]) 
                start--;
                count++;
            
        
        return count;
    

 那怎么证明这么做是可以的呢？找个数学专业的问问吧，我们解决到这一步就足够了