f(x)=(sinx)^2展开成x的幂级数

Posted 2023-04-28

简单计算一下即可，答案如图所示

参考技术A 用指数函数对sinx进行变换：sinx = (e^(ix)-e^(-ix))/(2i) （1）

那么sin^2(x)也就是上面（1）式子的平方，将上式平方展开后，得到的计算结果为：
-1/4 * (e^(2ix) + e^(-2ix)) + 1/2 （2）

有因为 e^x = Sum_k=1^Infinity (x^k)/k! （3）（这个式子代表对(x^k)/k!求和，从k=1到正无穷。
那么将（2）式中的2ix和-2ix带入到（3）式中能得到级数表达式，最后整理（2）式即可。本回答被提问者和网友采纳 参考技术B 你直接用sinx的麦克劳林级数整体平方不就行了 这不是显而易见的吗 sinx=t 那sinx 的平方=t^2

级数入门泰勒级数

多项式函数是长这样的函数：

[f(x)=a_0+a_1x+a_2x^2+ldots+a_nx^n]

它有一个很(Nice)的特点：代人(x)，在(O(n))的时间内就可以求出(f(x))，没有任何障碍.

但是这样的函数：

[g(x)=e^x]

[h(x)=sin x]

想得到(g(3))或是(h(7))就比较困难了。因此我们需要用多项式函数去"取代"这些奇怪的函数。

逼近(f(x)=e^x)在x靠近0时的函数值

step1：用(y=a_0+a_1x)去逼近它.

具体的方法是让它的斜率等于(f(x))在(x=0)时的导数：1

让直线过((0,1))，于是得到的直线(y=x+1)

效果如下图：

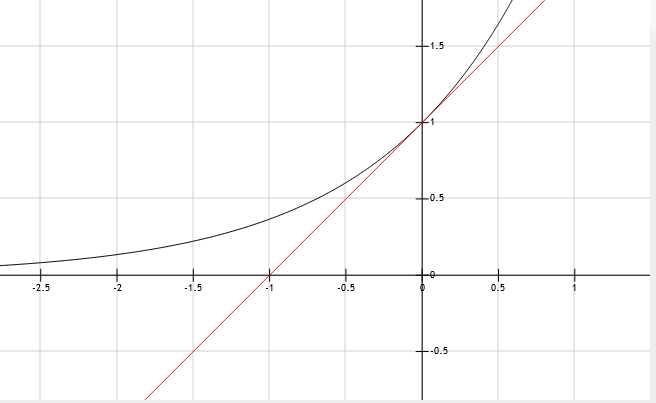
在(x)离(0)很近的时候还是比较精确的.

step2：用(g(x)=a_0+a_1x+a_2x^2)这个二次多项式去逼近它.

具体方法是让它在(x=0)处的函数值、导数值、二阶导数值与(f(x))相等.

[f(x)=e^x,f(0)=1]

[f'(x)=e^x,f'(0)=1]

[f''(x)=e^x,f''(0)=1]

再看这个二次多项式：

[g(x)=a_0+a_1x+a_2x^2,g(0)=a_0]
[g'(x)=a_1+2a_2x,g'(0)=a_1]
[g''(x)=2a_2,g''(0)=2a_2]

因为要让(f(x),f'(x),f''(x))与(g(x),g'(x),g''(x))分别对应相等，所以：

[a_0=1,a_1=1,2a_2=1]

所以(g(x)=1+x+frac{x^2}{2})

效果如下图.

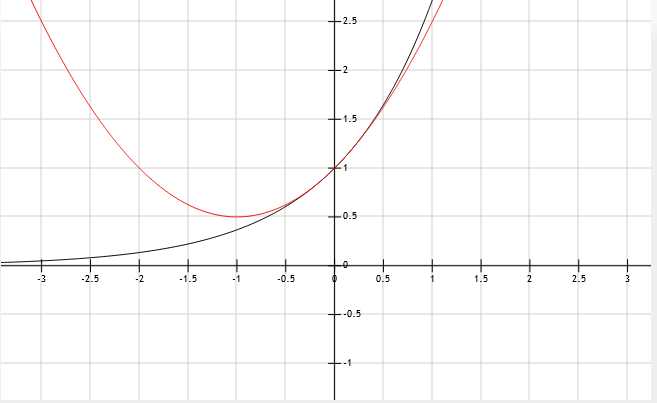
已经非常接近了呢.

step3：用(g(x)=a_0+a_1x+a_2x^2)这个二次多项式去逼近它.