GWAS基本建模原理

Posted 2023-04-27

参考技术A

我们说的混合线性模型主要是由固定效应和随机效应所构成的，固定效应是我们主要研究的影响因素，而随机效应是潜在的，影响固定效应的因素。
对于混合线性模型来说，随机效应对固定效应的影响有两种：
一种是：
随机效应通过影响固定效应的截距，从而产生对固定效应的影响，我们把这个称为层次影响

第三种是：

这里参考了某大佬写的 ，GWAS利用的原理既是混合线性模型，如果是加型效应：
我们先看下不考虑随机效应的：

那么上图就构成了一元回归里面的数据点
我们的任务就是，找到合适的a，b使得：

最小，所以根据最小二乘法，对每一个回归系数求偏导，得到正规方程组，求解即可。

考虑随机效应，那么模型就变成了：

αx为固定效应项，zβ为随机效应项，β为设计矩阵，z为随机效应的变量
那么我们设计好矩阵，即哪一个表型受随机因素的影响：

根据最小二乘法对每一个回归系数求偏导，得到正规方程组，求解α，β系数矩阵即可

根据《Population structure in genetic studies: Confounding factors and mixed models》提到的建模方式

如果SNP没发生突变， Xjk取下面的式子，对应strain A，B ：

如果SNP发生一种碱基的突变， Xjk取下面的式子，对应strain D，E ：

如果两个SNP发生两种碱基的突变， Xjk取下面的式子对应strain C ：

事实上这一步的主要目的还是把因子型变量转换为数值型变量，方便线性建模

回顾下模型：

e为随机因素

比方说目前有一个高血压的SNP的数据：

每一条序列可以看作是一个品种（处理），每一个品种（序列，处理）对应着不同的血压值。

那么以SNP为决策变量，不同的血压值为响应变量建立线性模型，当模型回归系数不为0，那么说明该SNP位点与血压这个性状有关联

这里有两个基本假设：第一个假设是H0假设，该假设也被称为null hypothesis，它认为SNP和性状没有关联，也即是说，性状 y 等于总体平均与环境因素的加和。
第二个假设是H1假设，该假设认为SNP和性状存在关系，也就是说当存在某个SNP的时候，某个性状或某个疾病会倾向于发生在该个体身上，β是指该SNP对性状影响的大小，也就是说， β越大，该SNP对性状的影响越大
显然left SNP对性状的影响更明显

为了让模型效果更好，作者引入了 u ，作为非模型因素

参考：
全基因组关联分析（GWAS）的计算原理

《Population structure in genetic studies: Confounding factors and mixed models》

David课件
https://genepi.qimr.edu.au/staff/davidD/Course/

备战数学建模20-BP神经网络算法

目录

一、BP神经网路基本原理

1-神经网络的简单介绍

2-神经网络模型

3-BP神经网络基本原理

4-神经网络的应用

二、BP神经网络编程实践

1-神经网络应用于分类问题的编程实例

2-神经网络应用于预测问题的编程实例

---

一、BP神经网路基本原理

1-神经网络的简单介绍

神经网络就是构建输入和输出的一个关系，而这个关系不能通过先验经验进行构建，神经网路通过一个黑箱的关系构建输入和输出的关系，黑箱的关键在于连接权的构建，神经网络一般包含三层，输入层，隐藏层，输出层，输出数据由标准输出数据和实际输出数据，我们需要对神经网络进行训练，训练过程就是通过调整连接权减少输出数据和标准数据之间的误差。神经网络可以用在数学建模的评价，预测，拟合，以及其它工业、经济各个领域。

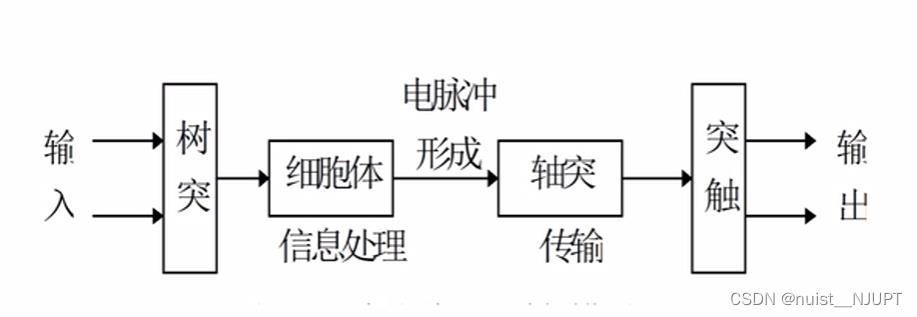
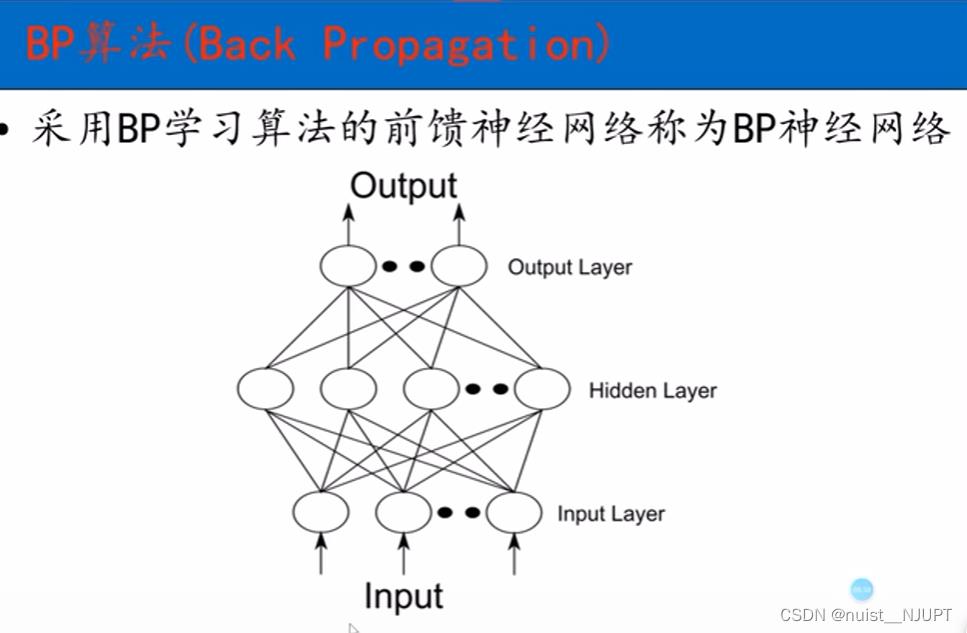
一个神经网络一般由三层组成，即输入层，隐藏层和输出层；输入层一般由一个个神经元组成，隐藏层是很必要的。 

 

 

 

 

 y和x尽建立一种权关系，权重可以调整，不用假设y与x的具体关系，神经网络相当于黑箱模型。 对于阈值，就是临界值，能够让大脑产生刺激的最低信号值。

 

2-神经网络模型

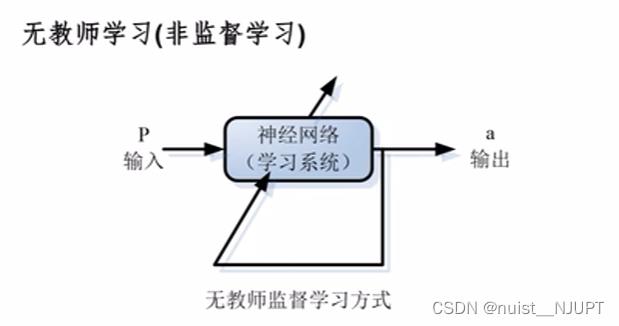
前馈：容易造成误差，自组织：容易产生混乱，反馈神经网路：相对好一些。

 

 

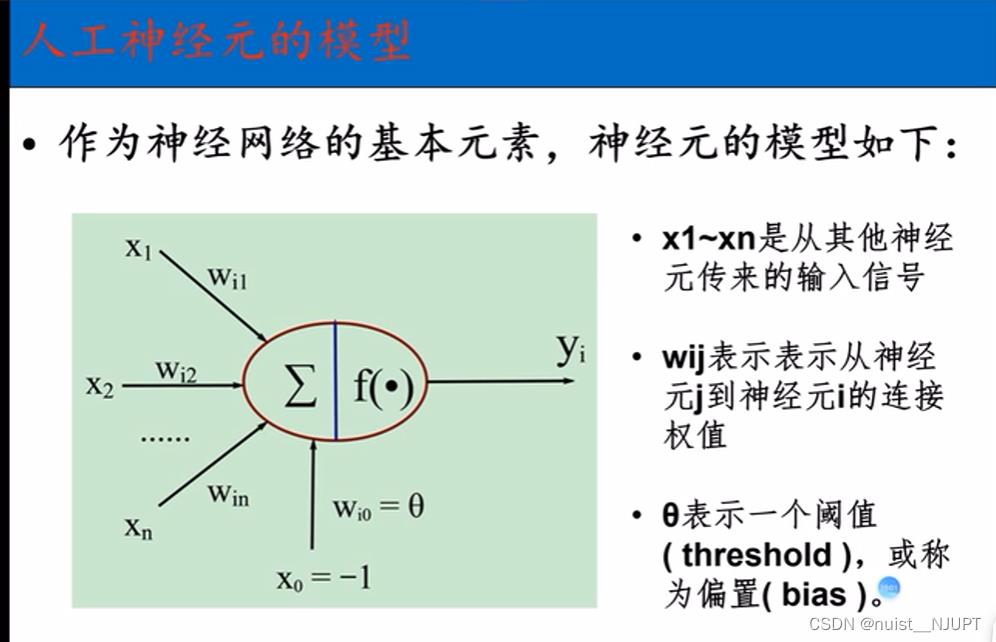
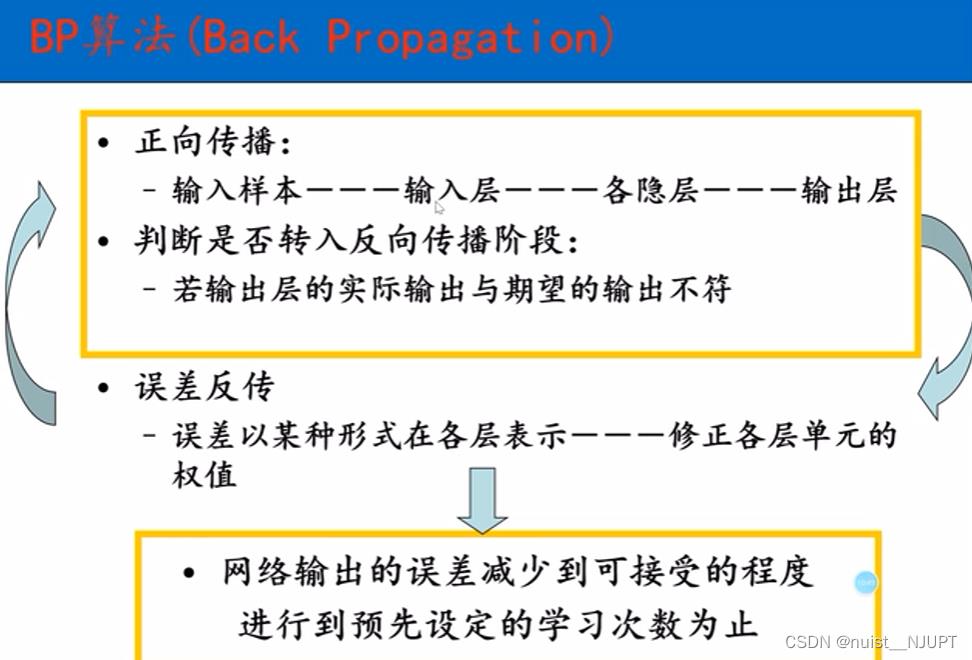
3-BP神经网络基本原理

我们可以知道：输入神经元的输入是固定的，神经元的数量与处理方式也是固定，标准输出是固定，阈值也往往是固定，就是权值是不固定的，只要权值构建好，结果就会好。

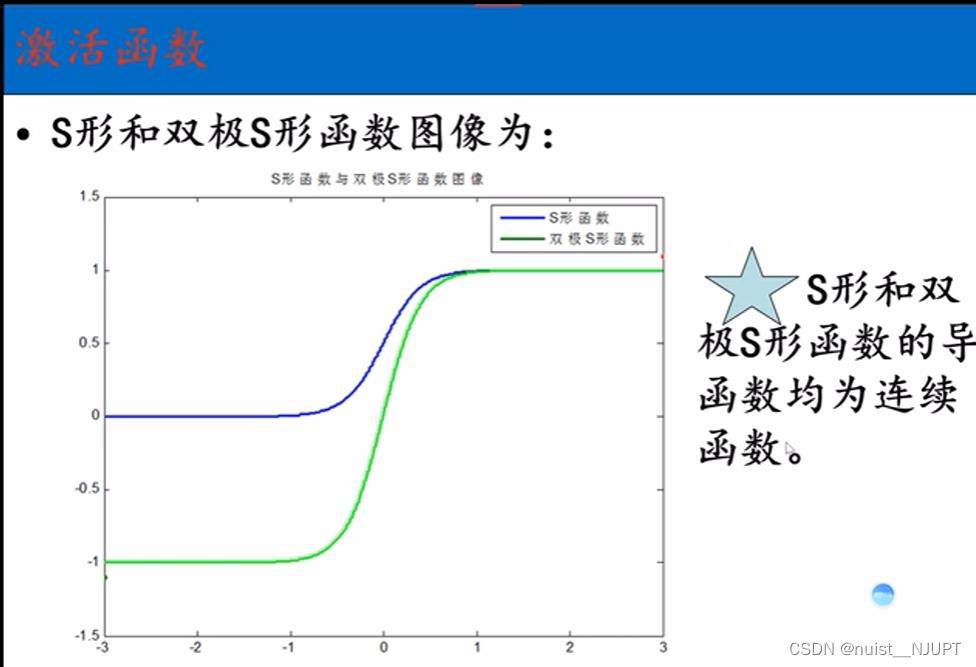
 对于每次输入后，经过激活函数激活后输出，具体如下所示：

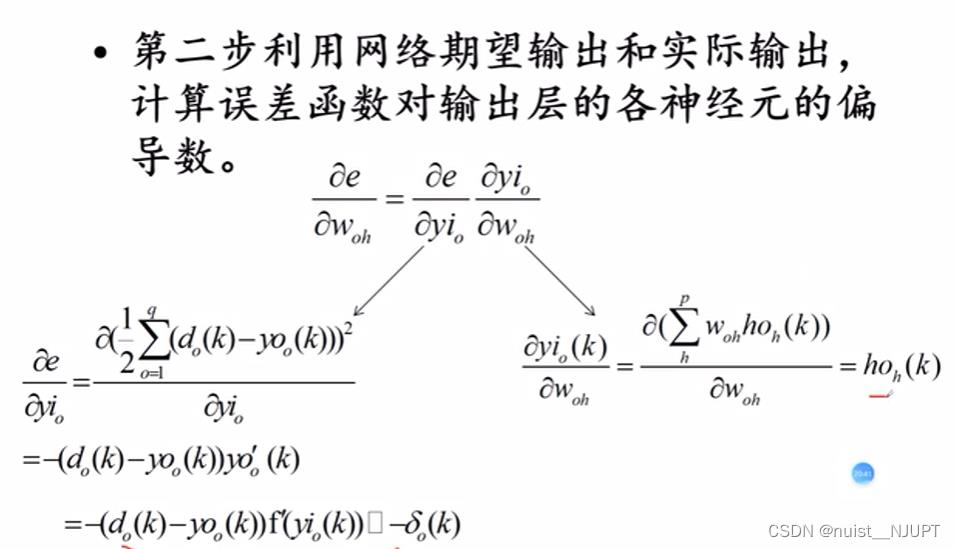
 我们最终是想知道误差取得最小值的时候，我们的权值的取值是多少。只需要误差对权值求导，找到导数等于0的点。

 

 

4-神经网络的应用

二、BP神经网络编程实践

1-神经网络应用于分类问题的编程实例

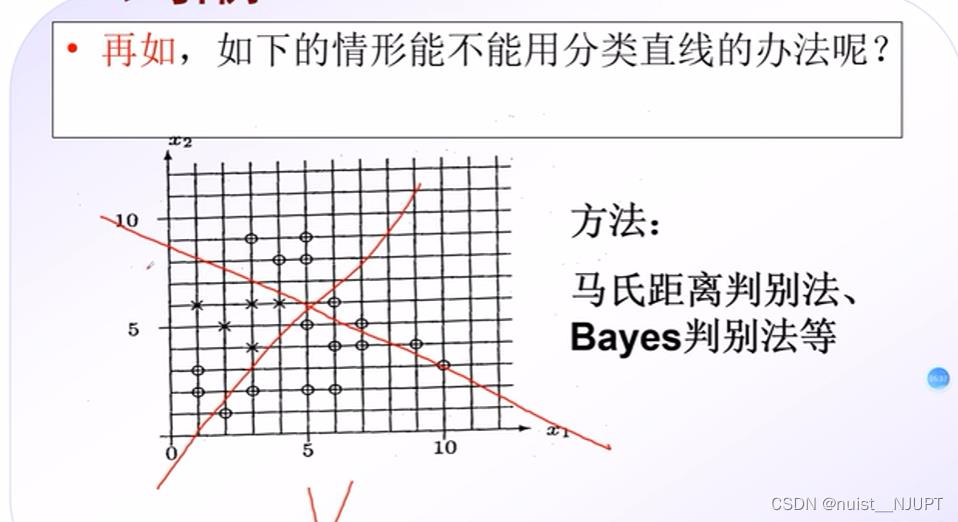
根据聚类思想，进行划分，画一条直线进行区分。

 但是大多数情况，一条直线很难区分数据的类别。

下面的新思路就可以通过神经网络模型进行构建：

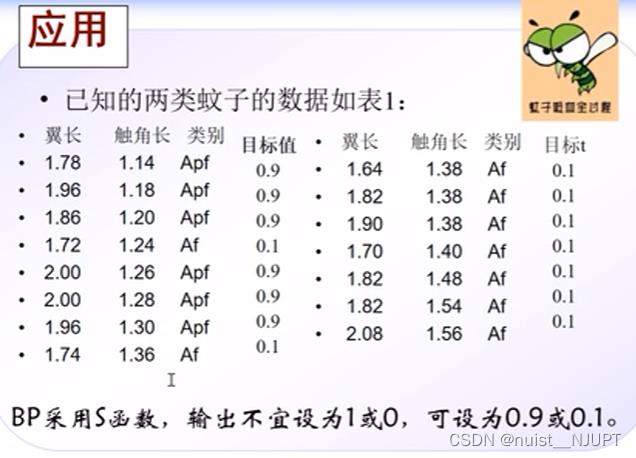
通过下表我们可以看到输入包含两个数据，即翼长和触角长，输入数据是15个，故输入数据P的维度是2*15，需要转置一下，输出数据t的维度是1*15，也需要转置一下。

上述分类问题的神经网络MATLAB代码如下所示：

clear; clc
P = [1.78, 1.96, 1.86, 1.72, 2, 2, 1.96, 1.74, 1.64, 1.82, 1.9, 1.7, 1.82, 1.82, 2.08; 
    1.14, 1.18, 1.2, 1.24, 1.26, 1.28, 1.3, 1.36, 1.38, 1.38, 1.38, 1.40, 1.48, 1.54, 1.56] ;
T = [0.9, 0.9, 0.9, 0.1, 0.9, 0.9, 0.9, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1] ;
%利用minmax函数求输入样本范围 
net = newff(minmax(P),[7,1],'tansig','purelin','trainlm');
net.trainParam.show=50; %每次循环50次
net.trainParam.epochs=10000;%最大循环10000次
net.trainParam.goal=0.01; %期望目标误差最小值
[net,tr]=train(net,P,T);%对网络进行反复训练


%对已知样本通过训练好的模型进行预测
Y = sim(net, P) ;
disp('输出预测的类别，靠近0.1的为Af类，靠近0.9的为Apf类：') ;
disp(Y) ;

%用训练好的模型进行预测
p = [1.3; 1.2] ;
s = sim(net, p) ;
disp('对翼长为1.3，触角长为1.2的进行类别预测：') ;
disp(s) ;

2-神经网络应用于预测问题的编程实例

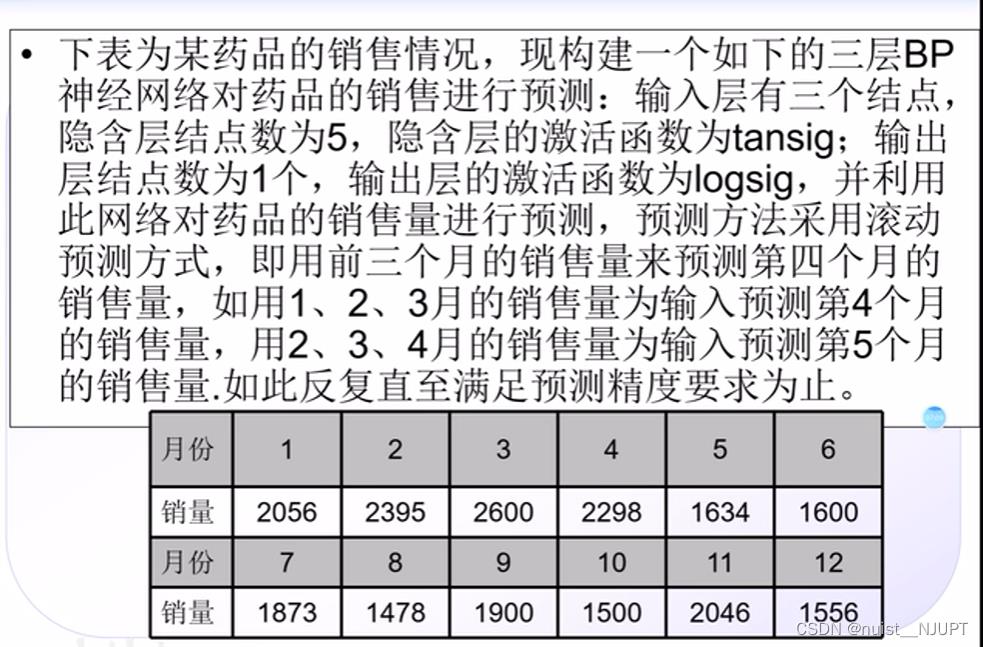
如下表预测问题，我们可以考虑一下怎么构建神经网络，让1，2，3月作为输入，4月的作为输出，2，3，4作为输入，5月份作为输出，依次类推。我们利用销量自身建立关系，而不是销量和月份建立关系。

前8个月的作为输入输出数据，输入数据3*6维，输出数据1*6维，进行训练，后面几个月作为预测数据进行预测。

上述预测过程的MATLAB代码如下所示：

clear; clc
P = [2056, 2395, 2600; 2395, 2600, 2298; 2600, 2298, 1634; 2298, 1634, 1600; 1634, 1600, 1873; 1600, 1873, 1478] ;
T = [2298, 1634, 1600, 1873, 1487, 1900] ;
P  = P' ;
ma = max(max(P)) ;
mi = min(min(P)) ;
%数据归一化到0-1之间
T = (T - min(min(P))) ./ (max(max(P)) - min(min(P))) ;
P = (P - min(min(P))) ./ (max(max(P)) - min(min(P))) ;

net = newff([0,1;9,1;0,1],[7,1],'tansig','logsig','traingd');
net.trainParam.show=50; %每次循环50次
net.trainParam.epochs=15000;%最大循环15000次
net.trainParam.goal=0.01; %期望目标误差最小值
[net,tr]=train(net,P,T);%对网络进行反复训练

%用原始数据做仿真
y = sim(net, P) ;
disp(y) ;
disp('4-9月份的预测结果为：') ;
y1 = y .* (ma - mi) + mi ;
disp(y1) ;

%输入9，10，11月份的数据，对12月份的数据进行预测
p = [1900, 1500, 2046] ;
p = p' ;
p = (p - mi) ./ (ma - mi) ;
r = sim(net, p) ;
disp('12月份的预测结果：') ;
disp(r) ;
disp('12月份反归一化后的结果如下：') ;
r1 = r * (ma - mi) + mi ;
disp(r1) ;

总结一下吧：对于构建输入和输出关系的情况，并且数据量比较大的情况下的非线性拟合，我们可以考虑使用神经网络。

神经网络在数学建模中一般用于分类，评价，预测类问题。

神经网络编程步骤：
1）寻找对结果产生影响的各种指标，假设有m个；
2）寻找样本n个，构造矩阵m*n，其对应的标准输出是n*1；
3) 将上述m*n与n*1分别带入网络中训练；
4）输入新的数据进行仿真。