中国剩余定理推广到 模数不是两两互素之后,在有解的情况下 怎样求解?求高手指点,说的详细点。谢谢!
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了中国剩余定理推广到 模数不是两两互素之后,在有解的情况下 怎样求解?求高手指点,说的详细点。谢谢!相关的知识,希望对你有一定的参考价值。
比如:有一数 模6余4,模8余2,模9余7,求该数
参考技术A 求所有模数的最小公倍数中国剩余定理中 模不一定互素的情形 只好两两合并
中国剩余定理
2016.1.26
由于比较懒,于是先copy百度一发
-------------------我是分割线--------------------
用现代数学的语言来说明的话,中国剩余定理给出了以下的一元线性同余方程组:
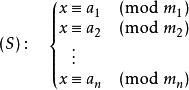
有解的判定条件,并用构造法给出了在有解情况下解的具体形式。
中国剩余定理说明:假设整数m1,m2, ... ,mn两两互质,则对任意的整数:a1,a2, ... ,an,方程组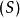 有解,并且通解可以用如下方式构造得到:
有解,并且通解可以用如下方式构造得到:
设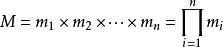 是整数m1,m2, ... ,mn的乘积,并设
是整数m1,m2, ... ,mn的乘积,并设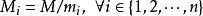 是除了mi以外的n- 1个整数的乘积。
是除了mi以外的n- 1个整数的乘积。
设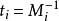 为
为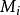 模
模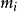 的数论倒数
的数论倒数 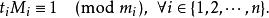 :
:
方程组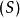 的通解形式为
的通解形式为
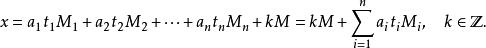 在模
在模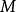 的意义下,方程组
的意义下,方程组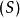 只有一个解:
只有一个解:
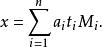
-------------------我是分割线--------------------
设来设去一大堆容易把人搞晕了,但是如果先看最后的式子就好理解了。
显然除了aitiMi这一项外,其余项模mi都得0,又因为ti是Mi的逆元,所以x mod mi=ai
于是就都符合我们求的一元同余线性方程组啦~
例题:解一元同余方程组
以上是关于中国剩余定理推广到 模数不是两两互素之后,在有解的情况下 怎样求解?求高手指点,说的详细点。谢谢!的主要内容,如果未能解决你的问题,请参考以下文章
POJ2891 Strange Way to Express Integers 不互质中国剩余定理