N条直线最多可以把一个平面分成几部分？ 的解题步骤

Posted 2023-03-22

当直线为n条时，把平面最多分成（n²+n+2）/2部分。

解析：通过已知探究结果，写出一般规律，当直线为n条时，把平面最多分成1+1+2+3+…+n，求和即可。通过已知探究结果，当直线为n条时，把平面最多分成：1+1+2+3+3+…+n=（1+n）n/2+1=（n²+n+2）/2。

平面与直线的关系：

1、点A在平面α内，记作A∈α；点B不在平面α内，记作B∉α。

2、点P在直线l上，记作P∈l；点P在直线l外，记作P∉I。

3、如果直线l上的所有点都在平面α内，就说直线l在平面α内，或者平面α经过直线l，记作l⊂α，否则说直线l在平面α外，记作l⊄α。

4、平面α、β相交于直线l，记作α∩β=l。

5、直线a在平面α内 记作 a⊂α。

参考技术A

第1条分成2个,

第2条分成4个,

第3条分成7个,

第4条分成11个,

第2条比第1条多分2个,

第3条比第2条多分3个

第4条比第3条多分4个

所以第n条,比第n-1条多分n个.

第2条的个数:4=2+2

第3条的个数:7=2+2+3

第4条的个数:11=2+2+3+4

第n条的个数:=2+2+3+4+ ----- +n

2+2+3+4+ ----- +n

=1+1+2+3+4+ ---- +n

=1+n*(n+1)/2

当n=1时,1+n*(n+1)/2=2

当n=2时,1+n*(n+1)/2=4

当n=3时,1+n*(n+1)/2=7

所以n条直线把平面分成1+n*(n+1)/2个

扩展资料：

直线有无数条对称轴，其中一条是它本身，还有所有与它垂直的直线（有无数条）对称轴。在平面上过不重合的两点有且只有一条直线，即不重合两点确定一条直线。在球面上，过两点可以做无数条类似直线。

构成几何图形的最基本元素。在D·希尔伯特建立的欧几里德几何的公理体系中，点、直线、平面属于基本概念，由他们之间的关联关系和五组公理来界定。

参考技术B 一条直线可将一个平面分成2部分
1+1
二条直线可将一个平面分成4部分
1+1+2
三条直线可将一个平面分成7部分
1+1+2+3
……
N条直线可将一个平面分成1＋（1+2+3+…+N）＝（N平方+N+2）÷2 参考技术C 我认为应该是
n(n+1)
————
+
1
2
解题步骤：
1（1+1）
一条
————
+1=2
个面
2
2（2+1）
2条
————
+1
=4
个面
2
3（3+1）
3。
————
+1
=7个面
2
.
.
.
n（n+1)
n条
————
+1
2本回答被提问者采纳 参考技术D 1条，可以分成2个嘛
2条，4个！
3条，7个！
好了，根据这个，列个2次方程，解除的解析式就是规律了。
经过
（1,2）（2,4）（3,7）

算法设计与分析 实验四 综合实验

1.平面划分：一条直线可以把平面分成两部分，两条直线分成四部分。那么 n 条直线最多可以把平面分成几部分？

入：多组数据，每组数据一个正整数 1 ≤ n ≤ 1000。

入：3  5    出：7    16

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
using namespace std;
int main()
	int n,sum;
	while(cin>>n)
		sum=n*(n+1)/2+1;
		cout<<sum<<endl;
	
	return 0;
  

2.众数问题：给定含有n个元素的多重集合S，每个元素在S中出现的次数称为该元素的重数。多重集S中重数最大的元素称为众数。例如，S=1，2，2，2，3，5。多重集S的众数是2，其重数为3。对于给定的由n 个自然数组成的多重集S，计算S的众数及其重数。如果出现多个众数，请输出最小的那个。

入：输入数据的第1行是多重集S中元素个数n（n<1300000）；接下来的n行中，每行有一个最多含有5位数字的自然数。

出：输出数据的第1行给出众数，第2行是重数。

入：6 1 2 2 2 3 5    出：2 3

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector> 
using namespace std;
void getmax(int &mid,int &m, int a[],int n);
void split(int a[],int n,int &l,int &r);
int main() 
	int n,temp,k; int m=0; int max=0;
	cin>>n;
	int *a=new int[n];
	for(int i=0; i<n; i++) 
		cin>>a[i];
	
	sort(a,a+n);//数组排序
	int t=0;
	getmax(t ,m, a, n);
	cout<<t<<endl;
	cout<<m<<endl;
	return 0;

void getmax(int &mid,int &m, int a[],int n) 
	int l,r; split(a,n,l,r); int t = n/2; int temp = r - l;
	if(temp > m) 
		m = temp;
		mid = a[t];
	
	if(l+1 > m) 
		getmax(mid, m, a, l+1);
	
	if(n-r > m) 
		getmax(mid, m, a+r, n-r);
	

void split(int a[],int n,int &l,int &r) 
	int mid = n/2;
	for(l = 0; l<n; ++l) 
		if(a[l] == a[mid])
			break;
		
	
	for(r = l+1; r<n; ++r) 
		if(a[r] != a[mid])
			break;
		
	

3.切木棍：有n根长为，a1,a2⋯an​的木棍。对n根木棍总共切k​次（可以在任意点切割），即最后变成n + k根木棍。请输出各种切法得到的n + k​​​​根木棍中最长那根在各种切法中的最短值（答案需要向上取整）。

入：n​ k   出：整数     入： 2 3  7 9   出：4

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<stdio.h> 
using namespace std;
const int MAX=2e5+9;
int ll=0; int rr=2e9+10; int shuzu[MAX];
bool hanshu(int n,int mid,int k);
int main()
	int n,k,mid;
	while(cin>>n>>k)
		for(int i=0;i<n;i++)
			cin>>shuzu[i];
		
		while(ll+1<rr)
			mid=ll+rr>>1;
			bool temp2=hanshu(n,mid,k);
			if(temp2)
				rr=mid;
			else
				ll=mid;
			
		
		cout<<rr<<endl;
	
	return 0;

bool hanshu(int n,int mid,int k)
	int z1=0,z2;
	for(int i=0;i<n;i++)
		z2=(shuzu[i]-1+mid)/mid-1;
		z1=z1+z2;
		if(z1>k)
			return false;
		
	
	return true;

4.二进制数组。有一个数组，里面元素只有0或1，可以删除该数组中的一个元素，然后返回数组中最长连续的1的长度，若不存在，则返回0

入：第一行：数组长度n， 1<=n<=100000 第二行：n个0或1的数字

出：输出一个数字，最长的连续的1的长度

入：6    1 0 1 0 1 1      出：3

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm> 
using namespace std;
int main() 
	int n; int cun = 0;  int temp = 0; int left = 0; int right = 0;
	cin>>n;
	int *nums=new int[n];
	for(int i=0;i<n;i++)
		cin>>nums[i];
	
	while(right<n)
		temp+=nums[right]== 0? 1 : 0;
		if (temp>1) 
			temp-=nums[left]== 0? 1 : 0;
			left++;
		
		right++;
		cun=cun>(right-left-1) ? cun:(right-left-1);
	
	cout<<cun<<endl;
	return 0;

5.数字三角形：给出如下图的数字三角形，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

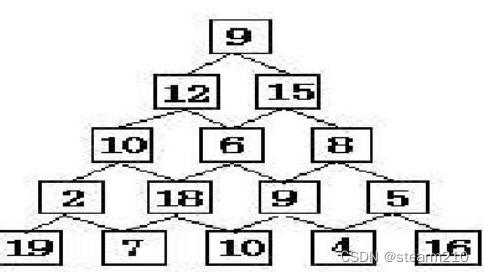
入：输入数据首先包括一个整数T,表示测试实例的个数。

每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度。

接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

入：1  5  7    3 8   8 1 0    2 7 4 4   4 5 2 6 5    出：30

 

#include<iostream>
#include<algorithm> 
using namespace std;
#define maxsize 110
int main() 
	int n,i,j,t;;
	int a[maxsize][maxsize];int sum[maxsize][maxsize];int id=1;
	cin>>t;
	for(int i=0; i<t; i++) 
		while(cin>>n) 
			for(i=1; i<=n; i++) 
				for(j=1; j<=i; j++) 
					cin>>a[i][j];
				
			
			for(i=1; i<=n; i++) 
				sum[n][i] = a[n][i];
			
			for(i=n-1; i>=1; i--) 
				for(j=1; j<=i; j++) 
					sum[i][j] = max(sum[i+1][j],sum[i+1][j+1])+a[i][j];
				
			
			cout<<sum[1][1]<<endl;
		
	
	return 0;

6.背包问题：n 种物品，每种物品有重量 w[i]、价值v[i]，数量不限，背包容量为 b。求背包能装物品最大价值。

入：每组数据第一行 n b，表示总共有 n 种物品和背包容量b，其中 1 ≤ n, b ≤ 1000。

接下来 n 行每行两个数 w[i]与v[i] 表示物品的重量与价值，其中 1 ≤ w[i] ≤ b， 1 ≤ v[i] ≤ 1000。

出：输出背包能装的最大价值。

入：4 10   2 1   3 3   4 5   7 9   出：12

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector> 
using namespace std;
int w[1020];//重量 int v[1020];//价值 int temp[1020][1020]; //动态规划表
int main() 
	int n,b;
	cin>>n>>b;
	for(int i=1; i<=n; i++) 
		cin>>w[i]>>v[i];
	
	for (int i = 1; i <=n; i++) 
		for (int j = 1; j <=b; j++) 
			if (j < w[i]) 
				temp[i][j] = temp[i - 1][j];
			 else 
				temp[i][j] = max(temp[i - 1][j], temp[i][j - w[i]] + v[i]);
			
		
	
	cout<<temp[n][b];
	return 0;

7.不同路径：一个机器人位于一个 m x n 网格的左上角，机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角，问总共有多少条不同的路径？

入：输入一行，包含由空格隔开的两个整数m，n（1<=m，n<=25），表示网格的长宽。

出：输出一行，表示从网格左上角到右下角总共有多少条不同的路径。

入：3  2     出3

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>	
using namespace std;
long long f[110][110];
int main() 
	long long m,n,i,j;
	cin>>m>>n;
    for(i = 0;i < m;i++)
    	f[i][0] = 1;
	
    for(j = 0;j < n;j++)
    	f[0][j] = 1;
	
    for(i = 1;i < m;i++)
        for(j = 1;j < n;j++)
            f[i][j] = f[i - 1][j] + f[i][j - 1];
        
    
	long long sum=f[m-1][n-1];
	cout<<sum<<endl;
	return 0;