Dance links算法

Posted 2020-11-09 Rogn

　　其实Dance links只是一种数据结构，Dance links 才是一种算法。dacing links x就是一个高效的求解该类问题的算法，而这种算法，基于交叉十字循环双向

链表。下面是双向十字链表的示意图：

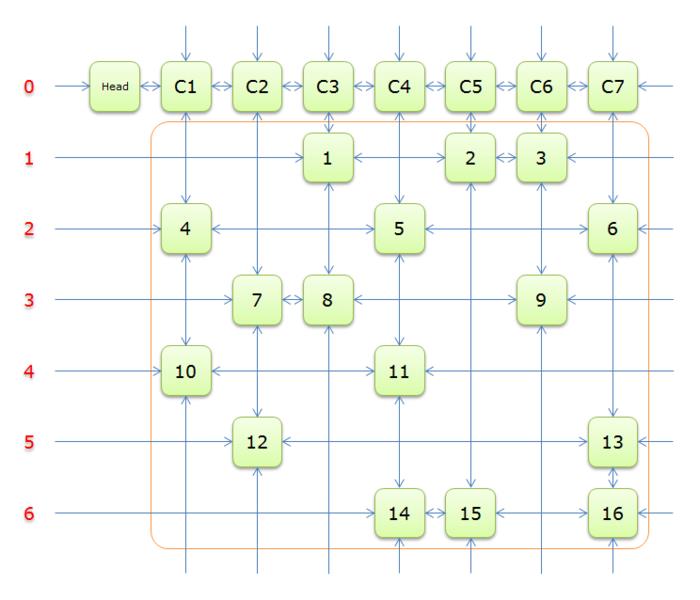
下面给一个使用这个算法模板的裸题：

Exact Cover

Description:

There is an N*M matrix with only 0s and 1s, (1 <= N,M <= 1000). An exact cover is a selection of rows such that every column has a 1 in exactly one of the selected rows. Try to find out the selected rows.

Sample Input:

6 7

3 1 4 7

2 1 4

3 4 5 7

3 3 5 6

4 2 3 6 7

2 2 7

Sample Output:

3 2 4 6

参考代码：

  1 #include<stdio.h>
  2 #include<iostream>
  3 using namespace std;
  4 const int maxnode = 1000 * 10 + 10;
  5 const int maxN = 1000 + 10;
  6 const int maxM = 1000 + 10;
  7 
  8 struct DLX {
  9     int n,m, size;                    //n行数，m列数，szie节点数
 10     int U[maxnode], D[maxnode], L[maxnode], R[maxnode], Col[maxnode], Row[maxnode];
 11     int H[maxN], S[maxM];            //H[i]第i行的第一个节点，S[j]第j列中节点的个数
 12     int ansd, ans[maxN];            //ansd解包含的行数，ans[]解
 13 
 14     void init(int _n, int _m)        //初始化十字链表
 15     {
 16         n = _n;
 17         m = _m;
 18         for (int i = 0; i <= m; i++)
 19         {
 20             Col[i] = i; Row[i] = 0;
 21             U[i] = D[i] = i;
 22             L[i] = i + 1; R[i] = i - 1;
 23             S[i] = 0;
 24         }
 25         R[0] = m; L[m] = 0;
 26         size = m;
 27         for (int i = 1; i <= n; i++)
 28             H[i] = -1;
 29     }
 30     void link(int r, int c)        //在第r行、c列插入一个节点
 31     {　　　　　　　　　　　　　　　　　　//注意，这里向下为方向
 32         size++;
 33         Col[size] = c;
 34         Row[size] = r;
 35         S[c]++;
 36         D[size] = D[c];
 37         U[D[c]] = size;
 38         U[size] = c;
 39         D[c] = size;
 40         if (H[r] == -1)
 41             H[r] = R[size] = L[size] = size;
 42         else
 43         {
 44             R[size] = R[H[r]];
 45             L[R[H[r]]] = size;
 46             L[size] = H[r];
 47             R[H[r]] = size;
 48         }
 49     }
 50     void remove(int c)            //移除第c列及列上节点所在的行
 51     {
 52         L[R[c]] = L[c];
 53         R[L[c]] = R[c];
 54         for (int i = D[c]; i != c; i = D[i])
 55             for (int j = L[i]; j != i ; j = L[j])
 56             {
 57                 D[U[j]] = D[j];
 58                 U[D[j]] = U[j];
 59                 --S[Col[j]];
 60             }
 61     }
 62     void resume(int c)        //恢复第c列及列上节点所在的行，与remove刚好相反
 63     {
 64         for(int i = U[c];i != c;i = U[i])
 65             for (int j = R[i]; j != i; j = R[j])
 66             {
 67                 ++S[Col[j]];
 68                 D[U[j]] = j;
 69                 U[D[j]] = j;
 70             }
 71         L[R[c]] = c;
 72         R[L[c]] = c;
 73     }
 74     bool Dance(int d)        //d为搜索的深度
 75     {
 76         if (R[0] == 0)
 77         {
 78             ansd = d;
 79             return true;
 80         }
 81         int c = R[0];
 82         for (int i = R[0]; i != 0; i = R[i])
 83             if (S[i] < S[c])
 84                 c = i;
 85         remove(c);
 86         for (int i = D[c]; i != c; i = D[i])    //逐个尝试
 87         {
 88             ans[d] = Row[i];
 89             for (int j = R[i]; j != i; j = R[j])
 90                 remove(Col[j]);
 91             if (Dance(d + 1))    return true;
 92             for (int j = L[i]; j != i; j = L[j])
 93                 resume(Col[j]);
 94         }
 95         resume(c);            //这个可有可无，写只是为了完整性
 96         return false;
 97     }
 98 };
 99 
100 DLX g;
101 int main()
102 {
103     int n, m;
104     
105     while (scanf("%d%d",&n,&m) == 2)
106     {
107         g.init(n, m);
108         for (int i = 1; i <= n; i++)
109         {
110             int num, j;
111             scanf("%d", &num);
112             while (num--)
113             {
114                 scanf("%d", &j);
115                 g.link(i, j);
116             }
117         }
118         if (!g.Dance(0))
119             printf("NO\\n");
120         else
121         {
122             printf("%d", g.ansd);
123             for (int i = 0; i < g.ansd; i++)
124                 printf(" %d", g.ans[i]);
125             printf("\\n");
126         }
127     }
128     return 0;
129 }

有什么不对的地方，多谢指教。