二叉搜索树的后序遍历序列——24

Posted 2020-07-12

    输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true，否则返回false。假设输入数组的任意两个数组都互不相同。

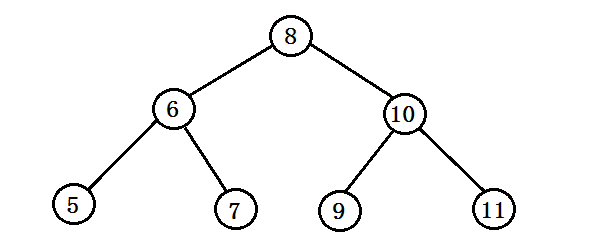
    二叉搜索树的特点就是每个结点的左子树的值都比自身的值小，而右子树的值都比自身值要大。比如如上的二叉搜索树后序遍历的结果就是{5,7,6,9,11,10,8}，但是题意并不是给出一棵二叉搜索树让判断数组是否为后序遍历序列，而是只有一组数据让判断是否为某个二叉搜索树的后序遍历结果，因此之能依据二叉搜索树后序遍历结果的特点来进行分析判断；

    就拿上面的结果来说，可以发现，因为是后序遍历，因此数组的最后一个结点一定是根结点，而因为是二叉搜索树，所以根结点前面的部分可以分为两块，一块都比根结点的值要小，因此为其左结点，而另一部分都比根结点的值要大，因此是根结点的右子树部分，然后可以用递归来再对左右子树部分进行判断，如果不满足上述的任一部分则返回false.....(balabalabala.......其实本来不是这个样子的，可是都要插入结果图片发布了突然网卡了，再恢复就发现什么都没有了系统没有保存，又重新开始写，不说了心好累5555555555555555很晚了要洗洗睡了 ，直奔程序吧 T_T)

程序设计如下：

#include <iostream>
using namespace std;

bool JudgeIsPostOrderOfBST(int *arr, size_t start, size_t end)//名字臭长臭长的 -_-
{
    bool ret = false;
    if((arr != NULL) && (start < end))//参数条件判断
    {
        size_t i = 0;
        for(; i < end; ++i)//在数组中查找第一个比根结点大的数，进行分块
        {
            if(arr[i] > arr[end])
                break;
        }

        size_t j = i;
        for(; j < end; ++j)//对分块之后的部分进行判断，如不满足直接返回false
        {
            if(arr[j] < arr[end])
                return ret;
        }
        if(j == end)//如果满足条件则当前状态为true，接着就需要进行递归判断左右子树部分
            ret = true;

        if(start < i-1)
            ret = JudgeIsPostOrderOfBST(arr, start, i-1);
        if(i < end-1)
            ret = JudgeIsPostOrderOfBST(arr, i, end-1);
    }
    return ret;
}

int main()
{
    int arr1[] = {5,7,6,9,11,10,8};
    int arr2[] = {4,5,2,6,7,3,1};

    cout<<JudgeIsPostOrderOfBST(arr1, 0, sizeof(arr1)/sizeof(arr1[0]-1))<<endl;
    cout<<JudgeIsPostOrderOfBST(arr2, 0, sizeof(arr2)/sizeof(arr2[0]-1))<<endl;
    return 0;
}

运行程序：

《完》

本文出自 “敲完代码好睡觉zzz” 博客，请务必保留此出处http://2627lounuo.blog.51cto.com/10696599/1782730