这次的比赛充满着玄学的气息,玄学链接
首先讲一下为什么没有第十四场
其实今天早上9点时看到题目就叫了:原题!
然后老叶就说换一套,但如果仅仅是这样就没什么
但等13min后结束这场考试后,一评测发现有人A了T1
但老叶并没有开启Unrated,然后大家集体垫底被踩
然后我就莫名掉了74Rating
但是之后第二场很快就开始了,但是等第二场测完之后还是没有进行Unrated处理,结果就白掉分了
真是Dog至极
然后讲一下题目,这次主要是T2炸了,花了蛮长时间写O(n^2)的玄学的,然后所有数据点中竟没有一个点的n小于5000(全是90000+)
但是T3莫名快速幂多得了40pts还是很令人欣慰的
T1
这道题无疑是本场最不可做的一道题
具体的满分算法需要二维树状数组 or 主席树来搞
这里就直接优化一下暴力得50pts就很优秀了
由于本题数据n的范围不大,可以直接埃式筛来搞
50CODE
#include<cstdio>
using namespace std;
const int N=100005,MAX_SIZE=1000005;
int a[N],n,q,l[N],r[N],x[N],y[N],max_num;
bool prime[MAX_SIZE];
inline char tc(void)
{
static char fl[100000],*A=fl,*B=fl;
return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
x=0; char ch=tc();
while (ch<\'0\'||ch>\'9\') ch=tc();
while (ch>=\'0\'&&ch<=\'9\') x=x*10+ch-\'0\',ch=tc();
}
inline void write(long long x)
{
if (x/10) write(x/10);
putchar(x%10+\'0\');
}
inline int max(int a,int b)
{
return a>b?a:b;
}
inline void get_prime(int m)
{
register int i,j;
for (prime[1]=1,i=2;i<=m;++i)
if (!prime[i]) for (j=i<<1;j<=m;j+=i) prime[j]=1;
}
inline long long work(int l,int r,int x,int y)
{
long long tot=0; register int i,j;
for (i=x;i<=y;++i)
if (!prime[i])
for (j=l;j<=r;++j)
{
int now=a[j];
while (!(now%i)) ++tot,now/=i;
}
return tot;
}
int main()
{
//freopen("A.in","r",stdin); freopen("A.out","w",stdout);
register int i;
for (read(n),i=1;i<=n;++i)
read(a[i]);
for (read(q),i=1;i<=q;++i)
read(l[i]),read(r[i]),read(x[i]),read(y[i]),max_num=max(max_num,y[i]);
get_prime(max_num);
for (i=1;i<=q;++i)
write(work(l[i],r[i],x[i],y[i])),putchar(\'\\n\');
return 0;
}
T2
这其实时一道比较经典的水题了
我们先考虑在一条直线上的情况,就是Luogu P1367
假设两只蚂蚁A,B面对面相遇:
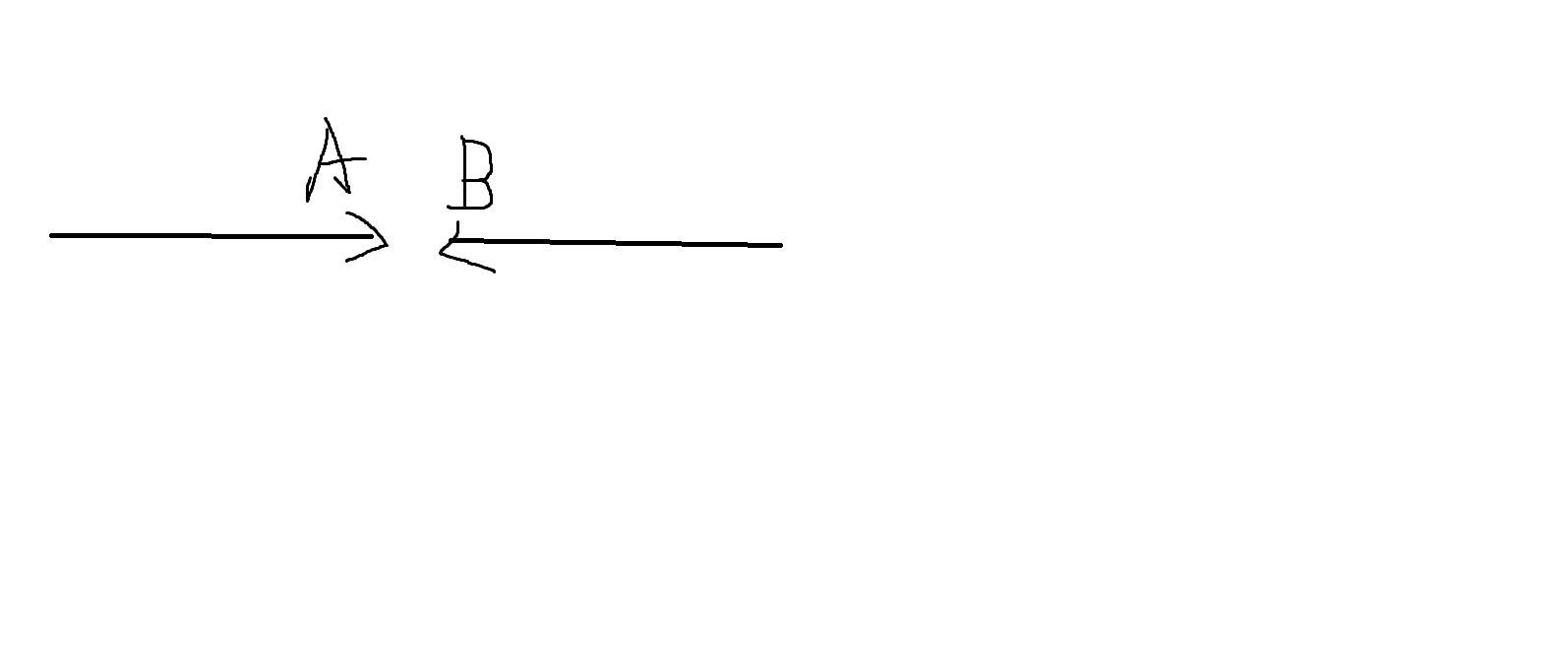
然后他们掉头,相当于穿过了对方并且互换身份:
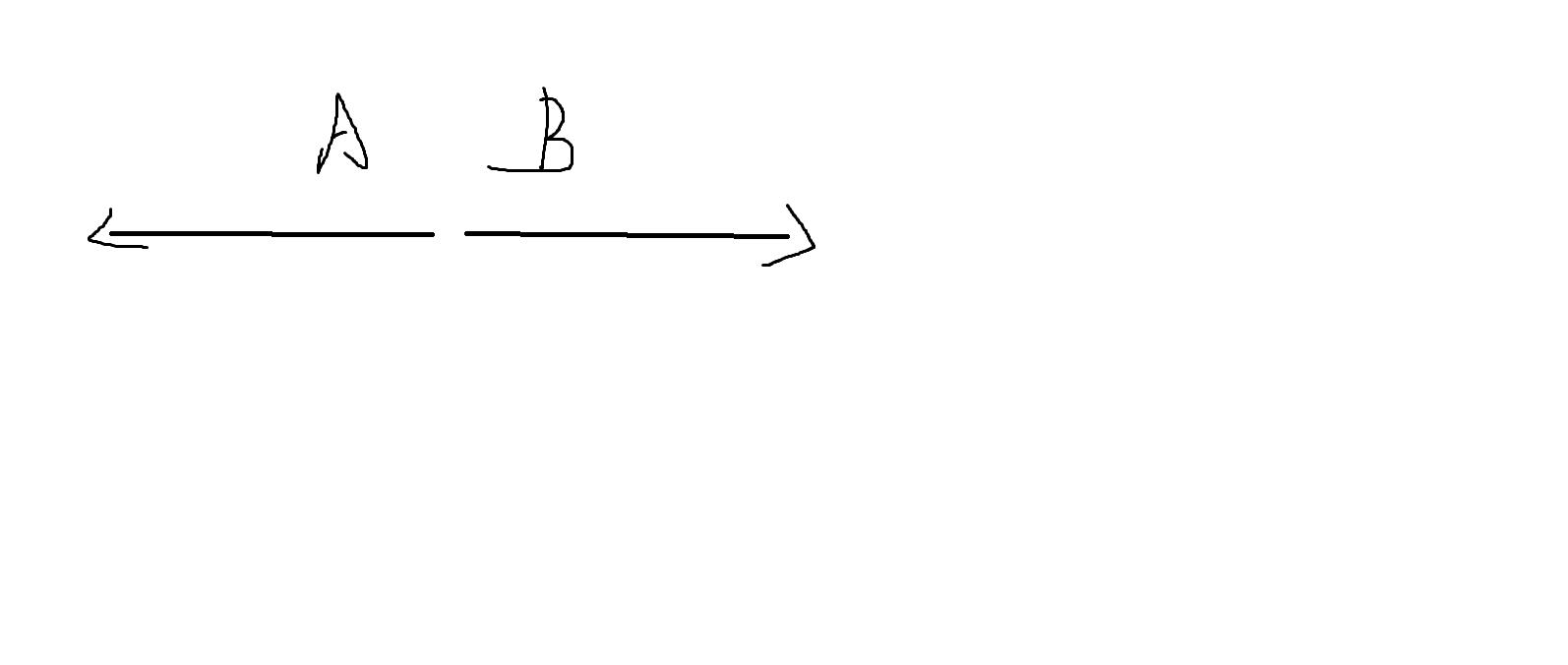
但是有一个性质:它们的相对位置不会改变
什么意思——就是不管它们怎么移动,第i只蚂蚁的左边一定是第i-1只蚂蚁,右边一定是第i+1只蚂蚁
然后只要sort一下就可以了
但是对于这道题是一个圆的情况,则有些在后面的蚂蚁可能会排到前面去
但是蚂蚁的位置还是不变,并且相对位置保持相对不变,因此我们只要知道第1只蚂蚁的位置就可以顺次求出后面蚂蚁的位置
我们设第一只蚂蚁的相对排名为cnt,初始值为1.每当一只蚂蚁从l-1到达0时,cnt++;每当一只蚂蚁从0爬到l-1时,cnt--
然后就排序后通过cnt正确输出顺序即可
因为当前HHHOJ没有开放这次题目,因此到Atcoder提交即可
CODE
#include<cstdio>
#include<algorithm>
const int N=1e5+5;
int a[N],n,l,t,x,w;
long long cnt=1;
using namespace std;
inline char tc(void)
{
static char fl[100000],*A=fl,*B=fl;
return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
x=0; char ch=tc();
while (ch<\'0\'||ch>\'9\') ch=tc();
while (ch>=\'0\'&&ch<=\'9\') x=x*10+ch-\'0\',ch=tc();
}
inline void write(int x)
{
if (x/10) write(x/10);
putchar(x%10+\'0\');
}
int main()
{
//freopen("B.in","r",stdin); freopen("B.out","w",stdout);
register int i;
read(n); read(l); read(t);
for (i=1;i<=n;++i)
{
read(x); read(w);
if (w==1) a[i]=(x+t)%l,cnt+=(x+t)/l; else a[i]=(x-t%l+l)%l,cnt-=t%l>x?t/l+1:t/l;
}
cnt=(cnt%n+n-1)%n+1;
sort(a+1,a+n+1);
for (i=cnt;i<=n;++i)
write(a[i]),putchar(\'\\n\');
for (i=1;i<cnt;++i)
write(a[i]),putchar(\'\\n\');
return 0;
}
T3
首先30pts的爆搜不讲
然后这题有一个性质:若n>=m,即ans为2^2m,因为就有所有的塔都有可能红或蓝
快速幂求之即可,结合爆搜可以得70pts
考虑DP,这里用r表示红的,b表示蓝的
我们首先发现,每一次操作的时候加上去的要么是"rr","rb","br","bb",而且手上红色蓝色的和总是为n
而且条件很简单,若第一位r则此时手上必须有1个r
然后我们设f[i][j]表示进行第i次操作时手上有j个红色的方案总数,则蓝的有n-j个
又发现这样可能会用重复的方案,然后我们发现:若对于两种状态,手上的红色个数不为0,那么它们就重复了
因此我们设f[i][j][0/1]表示此时红色的是否取完过,然后再转移即可
CODE
#include<cstdio>
#include<cstring>
using namespace std;
const int N=3005,mod=1e9+7;
int f[2][N][2],n,m,ans;
inline void inc(int &x,int y)
{
x+=y; x-=x>=mod?mod:0;
}
int main()
{
register int i,j,k;
scanf("%d%d",&n,&m);
for (i=1;i<=n;++i)
f[0][i][0]=1; f[0][0][1]=1;
for (i=0;i<m;++i)
{
int now=i&1,nxt=now^1;
memset(f[nxt],0,sizeof(f[nxt]));
for (j=0;j<=n;++j)
for (k=0;k<=1;++k)
{
if (j) inc(f[nxt][j-1][k|(j==1)],f[now][j][k]);
if (j) inc(f[nxt][j][k|(j==1)],f[now][j][k]);
if (n-j) inc(f[nxt][j+1][k],f[now][j][k]);
if (n-j) inc(f[nxt][j][k],f[now][j][k]);
}
}
for (i=0;i<=n;++i)
inc(ans,f[m&1][i][1]);
printf("%d",ans);
return 0;
}