二叉树的应用：求解四则运算

Posted 2020-10-31 Fate0729

一 二叉树如何表示四则运算

1.1 表达式转换为二叉树

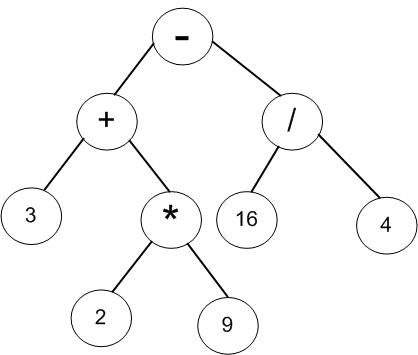
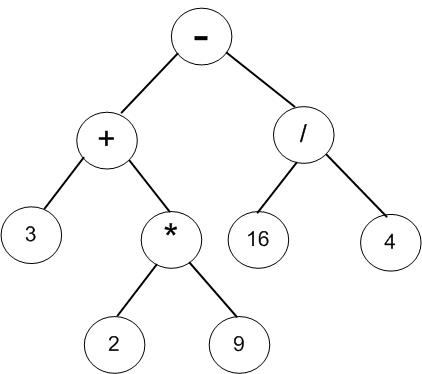
　　上图是表达式“3+2*9-16/4”转换成的二叉树，观察表达式，可以看出：

　　（1）操作数都是叶子节点；

　　（2）运算符都是内部节点；

　　（3）优先运算的操作符都在树下方，而相对优先级较低的减法（根节点）运算则最后运算。

　　从上往下看，这棵二叉树可以理解如下：

　　（1）要理解根节点"-"号的结果必须先计算出左子树"+"和右子树"/"号的结果。可以看，要想得到"+"号的结果，又必须先计算其右子树"*"号的结果；

　　（2）"*"号左右孩子是数字，可以直接计算，2*9=18。接下来计算"+"号，3+18=21，即根节点的左子树结果为21；

　　（3）"/"号左右孩子是数字，可以直接计算，16/4=4。于是，根节点的右子树结果为4。

　　（4）最后计算根节点的"-"号，21-4=17，于是得出了该表达式的值为17。

1.2 二叉表达式树的构造过程解析

 　　从上面的解析过程可以看出，这是一个递归的过程，正好可以用二叉树先序遍历的方法进行计算。下面我们来一步一步地通过图示来演示一下表达式"3+2*9-16/4"解析生成二叉树的过程。

　　（1）首先获取表达式的第一个字符“3”，由于表达式树目前还是一棵空树，所以3成为根节点；

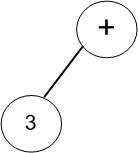
　　（2）获取第二个字符“+”，此时表达式树根节点为数字，需要将新节点作为根节点，原根节点作为新根节点的左孩子。这里需要注意的是：只有第二个节点会出现这样的可能，因为之后的根节点必定为操作符；

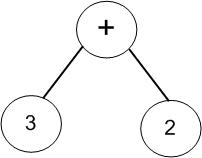
　　（3）获取第三个字符“2”，数字将沿着根节点右链插入到最右端；

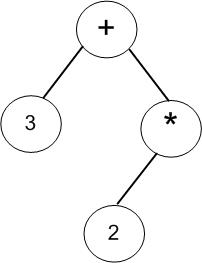
　　（4）获取第四个字符“*”，如果判断到是操作符，则将与根节点比较优先级，如果新节点的优先级高则插入成为根节点的右孩子，而原根节点的右孩子则成为新节点的左子树；

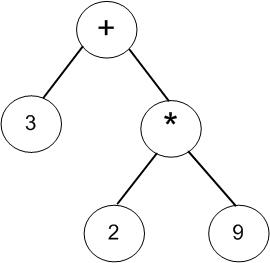
　　（5）获取第五个字符“9”，数字将沿着根节点右链插入到最右端；

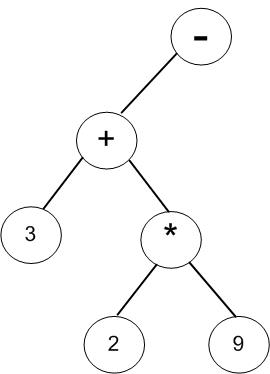
　　（6）获取第六个字符“-”，“-”与根节点“+”比较运算符的优先级，优先级相等则新节点成为根节点，原表达式树则成为新节点的左子树；

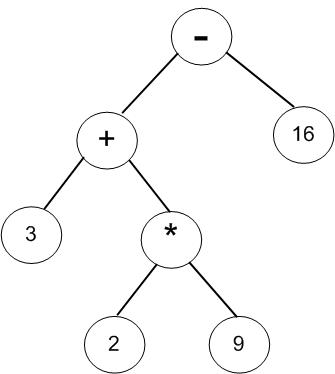
　　（7）获取第7与第8个字符组合为数字16，沿着根节点右链插入到最右端；

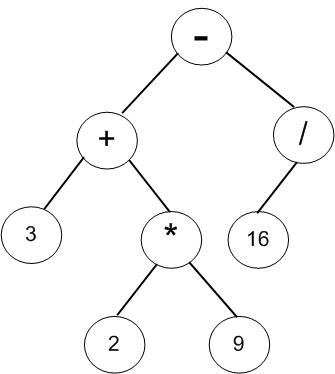
　　（8）获取第九个字符“/”，与根节点比较运算符的优先级，优先级高则成为根节点的右孩子，原根节点右子树则成为新节点的左子树；

　　（9）获取第十个字符“4”，还是沿着根节点右链查到最右端。至此，运算表达式已全部遍历，一棵表达式树就已经建立完成。

二 C++代码实现

#include "stdio.h"
#include <iostream>
using namespace std;

template <typename T>
struct BTreeNode
{
    T key;
    BTreeNode<T> *left;
    BTreeNode<T> *right;
    BTreeNode<T> *parent;
};

struct Operator
{
    char *cOperatorVal;
    int nPriority;
};

static Operator OPERATOR[] = {{"+", 1},{"-", 1},{"*", 2},{"/", 2}};
#define NUM_PRIORITY 10    // 自定义数字的优先级

template <typename T>
class BTree
{
public:
    explicit BTree() : m_pTree(NULL),m_pCurrentNode(NULL)
    {

    }
    ~BTree()
    {
        DestroyTree(m_pTree);
        m_pTree = NULL;
        m_pCurrentNode = NULL;
    }

    bool IsOperator(T key)
    {
        for (int i = 0; i < sizeof(OPERATOR)/sizeof(OPERATOR[0]); i ++)
        {
            if (0 == strcmp(key, OPERATOR[i].cOperatorVal))
            {
                return true;
            }
        }

        return false;
    }

    // 根据操作符得到其优先级
    int GetPriority(T key)  
    {
        for (int i = 0; i < sizeof(OPERATOR)/sizeof(OPERATOR[0]); i ++)
        {
            if (strcmp(key, OPERATOR[i].cOperatorVal) == 0)
            {
                return OPERATOR[i].nPriority;
            }
        }

        return NUM_PRIORITY;
    }

    BTreeNode<T>* AddNode(T key)
    {
        BTreeNode<T> *pNode = (BTreeNode<T> *)malloc(sizeof(BTreeNode<T>));
        pNode->key = key;
        pNode->parent = NULL;
        pNode->left = NULL;
        pNode->right = NULL;
        
        if (m_pTree == NULL)
        {
            m_pTree = pNode;
            m_pCurrentNode = pNode;
            return m_pTree;
        }

        // 若是数字，添加到上个结点的左边，若左边已有，则加右边
        // 若是运算符，首先比较和头结点云算法的优先级
        // (1)若为同优先级则当前运算符为新头结点，之前的为其左子树
        // (2)若为高优先级则为当前非符号的父节点，之前的为其左子树
        if (IsOperator(key))
        {
            if (GetPriority(key) <= GetPriority(m_pTree->key))
            {
                pNode->left = m_pTree;
                m_pTree->parent = pNode;
                m_pTree = pNode;
            }
            else
            {
                // 若操作符优先级很高
                pNode->parent = m_pCurrentNode->parent;
                if (m_pCurrentNode == m_pCurrentNode->parent->left)
                {
                    m_pCurrentNode->parent->left = pNode;
                }
                else
                {
                    m_pCurrentNode->parent->right = pNode;
                }

                pNode->left = m_pCurrentNode;
                m_pCurrentNode->parent = pNode;
            }
        }
        else
        {
            if (m_pCurrentNode->left == NULL)
            {
                m_pCurrentNode->left = pNode;
            }
            else
            {
                m_pCurrentNode->right = pNode;
            }

            pNode->parent = m_pCurrentNode;
        }
        m_pCurrentNode = pNode;
        return m_pTree;
    }

    void PreOrder(BTreeNode<T> * pNode)
    {
        if (pNode != NULL)
        {
            cout << pNode->key << " ";
            PreOrder(pNode->left);
            PreOrder(pNode->right);
        }
    }

    void MidOrder(BTreeNode<T> * pNode)
    {
        if (pNode != NULL)
        {
            MidOrder(pNode->left);
            cout << pNode->key << " ";
            MidOrder(pNode->right);
        }
    }

    void DestroyTree(BTreeNode<T> * pNode)
    {
        if (pNode != NULL)
        {
            DestroyTree(pNode->left);
            DestroyTree(pNode->right);
            free(pNode);
        }
    }
    
    // 计算
    int PreOrderCalc(BTreeNode<T> * pNode)
    {
        int num1, num2, result;
        if (IsOperator(pNode->key))
        {
            // 递归先序遍历计算num1
            num1 = PreOrderCalc(pNode->left);
            // 递归先序遍历计算num2
            num2 = PreOrderCalc(pNode->right);
            char optr = *(char *)pNode->key;

            switch (optr)
            {
            case \'+\':
                result = num1 + num2;
                break;
            case \'-\':
                result = num1 - num2;
                break;
            case \'*\':
                result = num1 * num2;
                break;
            case \'/\':
                if (num2 == 0)
                {
                    cout << "除数不能为0！" << endl;
                }
                result = num1 / num2;
                break;
            }

            return result;
        }
        result = atoi(pNode->key);
        return result;

    }

private:
    BTreeNode<T> *m_pTree;
    BTreeNode<T> *m_pCurrentNode;
};
void main()
{
    BTree<char *> tree;
    tree.AddNode("3");
    tree.AddNode("+");
    tree.AddNode("2");
    tree.AddNode("*");
    tree.AddNode("9");
    tree.AddNode("-");
    tree.AddNode("16");
    tree.AddNode("/");
    BTreeNode<char *> *pNode = tree.AddNode("4");
    
    cout << "前序遍历：";
    tree.PreOrder(pNode);
    cout << endl;

    cout << "中序遍历为表达式：";
    tree.MidOrder(pNode);
    cout << endl;

    int a = tree.PreOrderCalc(pNode);
    cout << "计算结果为：" << a <<endl;

    return;
}