求解具有n个结点的完全二叉树的深度，写出计算过程

Posted 2023-05-05

具有n个结点的完全二叉树的深度为「log2n」+1

计算过程如下：

采用数学归纳法证明。

当n=1=2^1-1时，命题成立。

假设当n<=2^k-1时具有n个结点的完全二叉树的深度为「log2n」+1,

则当n=2^k（以及2^k+1,...,2^(k+1)-1）时，由归纳假设知：

前2^k-1个结点构成深度为「log2n」+1的树；

再由完全二叉树的定义知：

剩余的1（或2,...,2^k)个结点均填在第「log2n」+2层上（作为“叶子”），深度刚好增加了1，

故n<=2^(k+1)-1时，命题成立。

扩展资料：

二叉树是一种树型结构，它的特点是每个结点至多只有二棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

二叉树的性质

1、在二叉树的第i层上至多有2i-1个结点；

2、深度为k的二叉树至多有2k-1个结点（k>=1）； 

3、对任何一棵二叉树T，如果其终端结点数为N0，度为2的结点数为N2，则N0=N2+1；

4、具有n个结点的完全二叉树的深度为「log2n」+1。

参考资料来源：百度百科—二叉树

参考技术A 具有n个结点的完全二叉树的深度为「log2n」+1 ！！！

二叉树的计算方法：

若一棵二叉树为空,则其深度为0,否则其深度等于左子树和右子树的最大深度加1,即有如下递归模型:

depth(b)=0 /*如果b=NULL*/

depth(b)=max(depth(b->left,b->right)+1 /*其它*/

因此求二叉树深度的递归函数如下:

int depth(btree *b)



int dep1,dep2;

if(b==NULL)return(0);

else

dep1=depth(b->left);

dep2=depth(b->right);

if(dep1>dep2)return(dep1+1);

else return(dep2+1);





二叉树的基本性质

★树的基本定义

1、树是n(n>=0)个结点的有限集

2、树的结点包含一个数据元素及若干指向其子树的分支

3、结点拥有的子树数称为结点的度

4、度为0的结点称为叶子或终端结点

5、树的度是树内各结点的度的最大值

6、结点的层次从根开始定义起，根为第一层，根的孩子为第二层

7、树中结点的最大层次称为树的深度或高度

8、如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中，最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。

★二叉树的定义

二叉树是一种树型结构，它的特点是每个结点至多只有二棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

★二叉树的性质

性质一 在二叉树的第i层上至多有2i-1个结点

性质二 深度为k的二叉树至多有2k-1个结点（k>=1）

性质三 对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1

性质四 具有n个结点的完全二叉树的深度为「log2n」+1

性质五 如果对一棵有n个结点的完全二叉树（其深度为「log2n」+1）的结点按层序编号（从第1层到第「log2n」+1层，每层从左到右），则对任一结点i（1≤i≤n），有

①如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲PARENT(i)是结点「i/2」

②如果2i>n，则结点n无左孩子（结点i为叶子结点）；否则其左孩子LCHILD(i)是结点2i

③如果2i+1>n，则结点i无右孩子，否则其右孩子RCHILD(i)是结点2i+1

★先序遍历二叉树的操作定义

若二叉树为空，则空操作，否则

(1)访问根结点

(2)先序遍历左子树

(3)先序遍历右子树

★中序遍历二叉树的操作定义

若二叉树为空，则空操作，否则

(1)中序遍历左子树

(2)访问根结点

(3)中序遍历右子树

★后序遍历二叉树的操作定义

若二叉树为空，则空操作，否则

(1)后序遍历左子树

(2)后序遍历右子树

(3)访问根结点本回答被提问者和网友采纳 参考技术B 具有n个结点的完全二叉树的深度为「log2n」+1 计算过程如下： 采用数学归纳法证明。当n=1=2^1-1时，命题成立。假设当n^k-1时具有n个结点的完全二叉树的深度为「log2n」+1, 则当n=2^k（以及2^k+1,.,2^(k+1)-1）时，由归纳假设知： 前2^k-1个结点构成深度为「log2n」+1的树；再由完全二叉树的... 参考技术C K层完全二叉树，就是前（K-1）层为满二叉树，第K层均为叶结点，可以不满。所以结点与深度的关系为：
2 ^ ( K - 1 ) - 1 < n <= 2 ^ K - 1。 所以K = [ ( n + 1 ) 以 2 为底取对数，然后向上取整 ]。 参考技术D 结论：⌊log2k⌋+1

二叉树

 二叉树的三种遍历

 

 

 

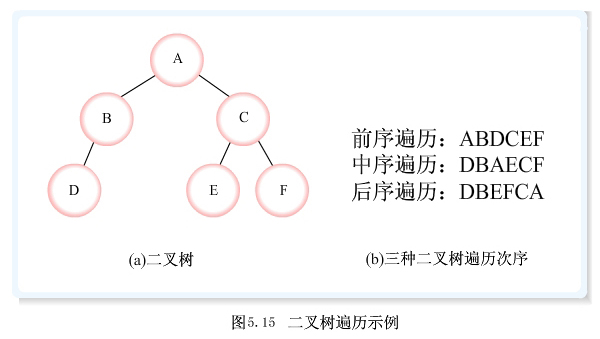
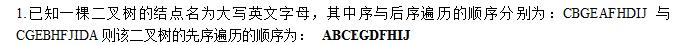
二叉树的有关计算

 

1.二叉树的深度和层数其实是一样的。
2.任意一棵树的总结点数等于总分支数+1
3.叶子结点也称叶子，度为0的结点。
4.一个深度为n的满二叉树的总结点数为 (2^(n-1))-1(其实得出这个结论画个图就知道了，不难)
5.深度为h的完全二叉树至少有2^(h-1）个结点，最多有（2^h）-1个结点。

相关题目：
1.一棵二叉树第六层（根结点为第一层）的结点数最多为？
其实这道题很简单，就是2^5=32

2.某二叉树中度为2的结点有18个，则该二叉树中有多少个叶子结点？
根据总结点数=总分支数+1，设叶子有n个，则有
18 + n = 18*2 + 1
n = 19

3.设一棵完全二叉树共有199个结点，那么该二叉树共有个分支结点？
思路就是先求出这个完全二叉树的叶子数，然后用总结点数减去叶子数就是分支结点的数目了。
因为有 (2^7) - 1<199<=(2^8)-1 
所以得深度为8，前7层为满二叉树，所以前7层的总结点数为(2^7) - 1 = 127 ,第7层的结点数为 2^6 = 64
则最后一层的叶子为 199 - 127 = 72 ，所以第7层的叶子数为 64 - 72/2 = 28
所以总叶子数为 72+28 = 100
分支数为 199 -100 = 99

4.在深度为7的二叉树中，最多有多少个叶结点？（注意这里问的是叶结点，而不是结点数，如果是结点数的话答案是（2^6）-1 ）
这种题目和例子1差不多，为 2^6

5.设一棵完全二叉树共有127个结点，那么该二叉树是满二叉树吗？
因为 一个深度为n的满二叉树的总结点数为 2^（n-1）-1
则设 2^（n-1）-1 = 127 
n = 8 ，所以这也是满二叉树。


6.具有53个结点的完全二叉树的深度为？
因为一个二叉树的结点数必然不会超过深度一样的满二叉树的结点数，所以有
(2^5)-1<53<=(2^6)-1 
所以答案为6

7.设一棵完全二叉树共有700个结点，则在该二叉树中有多少个叶子结点？
从第五题延伸出来的题目，由例6的思路得， (2^9)-1<700<=(2^10) - 1
所以得这棵二叉树前面9层是满二叉树，则得前9层的总结点数为 (2^9)-1 = 512 -1 =511
则剩下来的结点数就是最后一层的结点数，为 700 - 511 = 189 ，把他凑成偶数为190，则也就是说，
最后一层是从第九层中 190/2= 95个结点延伸出来的，所以第九层失去了95个叶子，又因为第九层的
结点数为 2^8 = 256，则第九层的叶子数为 256 - 95，则所有的结点数为256-95 +189 =350