概率图模型：贝叶斯网络

Posted 2020-07-10 -柚子皮-

http://blog.csdn.net/pipisorry/article/details/51461997

最大似然估计MLE

顾名思义，当然是要找到一个参数，使得L最大，为什么要使得它最大呢，因为X都发生了，即基于一个参数发生的，那么当然就得使得它发生的概率最大。

最大似然估计就是要用似然函数取到最大值时的参数值作为估计值，似然函数可以写做

Note: p(x|theta)不总是代表条件概率；也就是说p(x|theta)不代表条件概率时与p(x;theta)等价，而一般地写竖杠表示条件概率，是随机变量；写分号p(x; theta)表示待估参数（是固定的，只是当前未知）,应该可以直接认为是p(x)，加了;是为了说明这里有个theta的参数，p(x; theta)意思是随机变量X=x的概率。在贝叶斯理论下又叫X=x的先验概率。相乘因为它们之间是独立同分布的。

MLE通常使用对数似然函数

使用log-likelihood比原始函数好的原因：

1 由于有连乘运算，通常对似然函数取对数计算简便，即对数似然函数。it's kind of analytically nice to work with log-likelihood.

2 multiplying small numbers the numerical errors start to add up and start to propagate.If we are summing together small numbers,the numerical errors are not so serious.

3 log函数是单调的，所有东西保持不变。

最大似然估计问题可以写成

这是一个关于的函数，求解这个优化问题通常对求导，得到导数为0的极值点。该函数取得最大值是对应的的取值就是我们估计的模型参数。

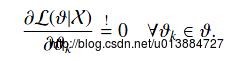
给定观测到的样本数据，一个新的值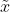发生的概率是

求出参数值不是最终目的，最终目的是去预测新事件基于这个参数下发生的概率。

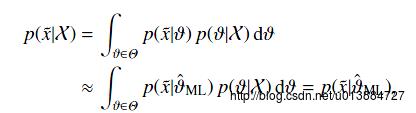
Note: 注意有一个约等于，因为他进行了一个近似的替换，将theta替换成了估计的值，便于计算。that is, the next sample is anticipated to be distributed with the estimated parameters θ ˆ ML .

扔硬币的伯努利实验示例

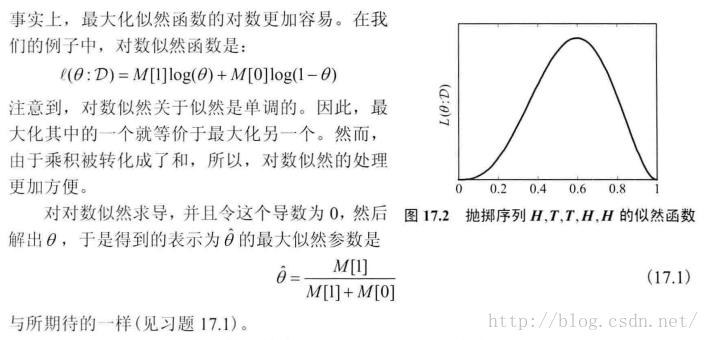
以扔硬币的伯努利实验为例子，N次实验的结果服从二项分布，参数为P，即每次实验事件发生的概率，不妨设为是得到正面的概率。为了估计P，采用最大似然估计，似然函数可以写作

其中表示实验结果为i的次数。下面求似然函数的极值点，有

得到参数p的最大似然估计值为

可以看出二项分布中每次事件发的概率p就等于做N次独立重复随机试验中事件发生的概率。

如果我们做20次实验，出现正面12次，反面8次，那么根据最大似然估计得到参数值p为12/20 = 0.6。

[Gregor Heinrich: Parameter estimation for text analysis*]

MLE的一个最简单清晰的示例

皮皮blog

最大似然估计MLE

能最大化已观测到的观测序列的似然的参数就是估计的参数值。

图钉的例子

为不同参数theta的可能值打分并选择的一种标准

一般情况下的MLE

最大似然准则

参数模型和参数空间

似然函数的定义

充分统计量

MLE的注解

MLE的缺陷：置信区间

似然函数度量了参数选择对于训练数据的影响。

似然函数的要求

[《Probabilistic Graphical Models：Principles and Techniques》(简称PGM)]

皮皮blog
from: http://blog.csdn.net/pipisorry/article/details/51461997

ref: