贝叶斯分类器(2)极大似然估计、MLE与MAP
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了贝叶斯分类器(2)极大似然估计、MLE与MAP相关的知识,希望对你有一定的参考价值。
参考技术A根据上一篇 贝叶斯分类器(1)贝叶斯决策论概述、贝叶斯和频率、概率和似然 ,我们对贝叶斯分类器所要解决的问题、问题的求解方法做了概述,将贝叶斯分类问题转化成了求解 的问题,并提出了第一个求解方法:极大似然估计,也对似然的概念做了一定的理解,在本篇中,我们来介绍极大似然估计的原理、使用方法及其与最大后验估计MAP的区别。
我们已经知道,似然即参数的似然,表示给定样本下,参数 为真值的可能性,所以,极大似然估计就是以最大化参数的似然值的方法来估计参数的真值的算法。
对于一批样本,共有M个属性值和N个类别,那么 就是一个M维向量,要求得 ,其实就是要求 ,因为对不同的类别 ,类条件概率 应该是不同的分布,所以应该有N个不同的分布假设和似然函数。
我们按极大似然估计的步骤来看看怎样计算
取对数得到对数似然函数,连乘转换为累加,求导之类的计算更加方便:
注意:
知乎上大神详细介绍了从散度的角度解读极大似然估计: 知乎 - 微调的回答 ,跟随大神的脚步学习一下(原回答了引入了期望,我觉得其实不用期望也没问题):
MLE的第一步是假设分布(或者已有一个分布),接下来就是通过最大化 发生的概率来求得分布参数,认为这就是最可能真实的分布,这个思路其实还是有一点绕的,凭什么说 发生的概率最大的参数就是真的参数呢?我们的目的是求出真实分布,最直观的思路应该是看我们 算出来的分布跟真实分布的相似程度 ,这刚好可以通过散度来解释。
这里的散度是机器学习的散度,也就是信息论中的散度,与物理上的散度不太一样。机器学习中我们常用的散度是KL散度(KL-Divergence)。信息论中, 可以理解为:用来衡量在同一份数据P下,使用P的编码方案和Q的编码方案的平均编码长度的差异,如果我们把真实的分布 和计算得到的分布 看做样本数据的编码方案,那么我们就可以用KL散度来计算两种分布之间的相似程度:
注意上面两个分布的顺序是不能变的,因为定义中的P必须是真实分布,数据就是由P产生的。我们的目标是人是让 最小,注意到式中 是定值,所以:
看上面的推导,再看看极大似然的公式:
是不是根本就是一样的?所以其实如果我们正向考虑极大似然估计,当模型是条件概率分布,损失函数是对数损失函数时,极大似然估计就是做 经验风险最小化 ;如果我们反过来考虑,即上面从散度推导的过程,MLE就是在寻找最接近真实分布的分布。
以上一篇提到的西瓜好坏分类为例:
西瓜数据集如下图:
显然样本共有 个属性值和 个类别,首先根据样本估计类先验概率 ,然后为每个属性估计条件概率 ,要求 ,应该假设两个六维概率分布,比如我们假设样本为6元正态分布:
均值向量 为6维向量,协方差矩阵 是一个6*6的正定矩阵。
然后分别写出似然函数的对数形式:
最后再求偏导解方程即可,多元正态分布求导计算还是挺复杂的,本篇主要讲极大似然估计,具体计算过程就不写了,大家明白是怎么做的就好。
讲完了极大似然估计的理论和操作,再来看看它和一个跟它很像的算法最大后验估计MAP的关系。
极大似然估计MLE是频率学派的参数估计方法,最大后验估计MAP是贝叶斯学派的参数估计方法。因此,同样是参数估计的问题,MLE中参数是确定值,故定义为 ;MAP中参数是一个随机变量,故定义为 ,是一个后验概率,受到先验 和样本 的共同作用,这就是他们最本质的区别了,由此可得到其计算过程的区别:
极大似然估计MLE对参数 的估计是:
最大后验估计MAP对参数 的估计是:
我们发现原来MAP与MLE在计算上的不同就是多了一个先验概率项,因此如果有一个合理的先验的话,MAP会比MLE对样本数据的依赖更小一些,如果数据量很大的话他们基本就是一样的了,以我们上一篇中的抛硬币例子来说:
如果按极大似然估计计算,取对数求导后计算得到 ,这似乎不太符合我们的常识,如果是用MAP呢?对抛硬币问题,我们先验是 (注意MAP中的 是随机变量,先验是一个分布,不能是一个数值哦,如果给一个数值的话,样本就不起作用了),因此:
正态分布的概率密度函数:
因此:
在MAP中使用一个高斯分布的先验的效果就类似于在MLE中采用L2正则,相当于 结构风险最小化 ,可以说,当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化就等价于最大后验估计。
回到 的计算上来, 进行取对数、求导,可得 ,结果受到了先验和样本共同的作用。
显然MAP的计算要麻烦的多,现实中很多问题都要比我们的例子复杂的多,其求解通常不会像我们的例子这样求导计算。
总结一下:
我们将贝叶斯分类器转化为了求解 的问题,使用极大似然估计是我们介绍的第一个求解方法,它还存在一些不足:
在下一篇中,我们来看看求解 问题的另一个方法:朴素贝叶斯。
主要参考资料
《机器学习》周志华
《统计学习方法》 李航
知乎 - 微调的回答
聊一聊机器学习的MLE和MAP:最大似然估计和最大后验估计
最大后验估计MAP
机器学习(二十五)— 极大似然估计贝叶斯估计最大后验概率估计区别
最大似然估计(Maximum likelihood estimation, 简称MLE)和最大后验概率估计(Maximum aposteriori estimation, 简称MAP)是很常用的两种参数估计方法。
1、最大似然估计(MLE)
在已知试验结果(即是样本)的情况下,用来估计满足这些样本分布的参数,把可能性最大的那个参数作为真实的参数估计。
也就是说,最大似然估计,就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值(模型已知,参数未知)。
(1)基本思想
当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大,而不是像最小二乘估计法旨在得到使得模型能最好地拟合样本数据的参数估计量。
例如,我们知道这个分布是正态分布,但是不知道均值和方差;或者是二项分布,但是不知道均值。 最大似然估计(MLE,Maximum Likelihood Estimation)就可以用来估计模型的参数。MLE的目标是找出一组参数,使得模型产生出观测数据的概率最大。
(2)模型推导
假设样本集D={x1 、x2 、…、xn},假设样本之间都是相对独立的,注意这个假设很重要!于是便有:
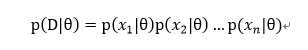
所以假设似然函数为:
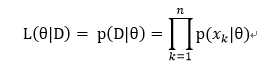
接下来我们求参的准则便是如名字一样最大化似然函数:
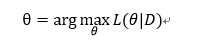
如果求得的θ 是参数空间中能使似然函数最大的取值,则θ是最可能的参数取值,即最大的似然估计值。
似然函数取对数:就是防止先验概率为0,那么上面的L(θ|D)整个式子便都成0 了,那肯定是不行的啊,不能因为一个数据误差影响了整个数据的使用。同时那么多先验概率相乘,可能出现下溢出。所以引入拉普拉斯修正,也就是取对数ln,想必大家在数学中都用过这种方法的。
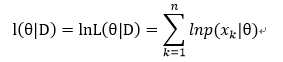
所以最大化的目标便是:
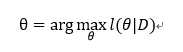
之后对参数求偏导,偏导数为0,求解最优值。
求最大似然函数估计值的一般步骤:
(1) 写出似然函数
(2) 对似然函数取对数,并整理
(3) 求导数
(4) 解似然方程
(3)推导举例
我们拿这枚硬币抛了10次,得到的数据(x0)是:反正正正正反正正正反。我们想求的正面概率θθ是模型参数,而抛硬币模型我们可以假设是 二项分布。那么,出现实验结果x0(即反正正正正反正正正反)的似然函数是多少呢?

对似然函数求对数,得到对数似然函数后对参数θ求导,令导数为0,求解θ的值。此处求得θ=0.7。
(4)最大似然估计的特点:
1.比其他估计方法更加简单;
2.收敛性:无偏或者渐近无偏,当样本数目增加时,收敛性质会更好;
3.如果假设的类条件概率模型正确,则通常能获得较好的结果。但如果假设模型出现偏差,将导致非常差的估计结果。
2、贝叶斯估计
贝叶斯统计的重点:参数未知且不确定,因此作为随机变量,参数本身也是一个分布,同时,根据已有的信息可以得到参数θ的先验概率,根据先验概率来推断θ的后验概率。
不同于ML估计,不再把参数θ看成一个未知的确定变量,而是看成未知的随机变量,通过对第i类样本Di的观察,使概率密度分布P(Di|θ)转化为后验概率P(θ|Di),再求贝叶斯估计。
贝叶斯估计是在MAP上做进一步拓展,此时不直接估计参数的值,而是允许参数服从一定概率分布。极大似然估计和极大后验概率估计,都求出了参数theta的值,而贝叶斯推断则不是,贝叶斯推断扩展了极大后验概率估计MAP(一个是等于,一个是约等于)方法,它根据参数的先验分布P(theta)和一系列观察X,求出参数theta的后验分布P(theta|X),然后求出theta的期望值,作为其最终值。另外还定义了参数的一个方差量,来评估参数估计的准确程度或者置信度。
贝叶斯估计:从参数的先验知识和样本出发。期望后延信息在真实的θ值处有一个尖峰。
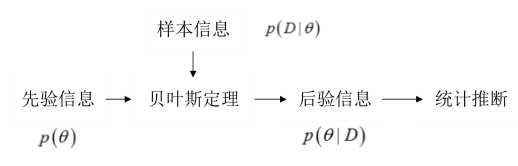
贝叶斯公式:
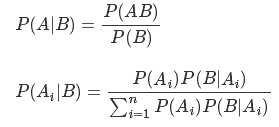
根据特征条件独立性假设:其中X 是多个特征的矩阵,Y 是类别标签
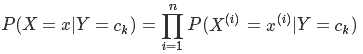
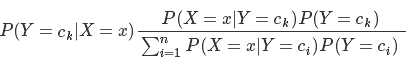
我们可以计算出任一样本x属于类别的概率,选择其中概率最大者便可作为其分类的类标。
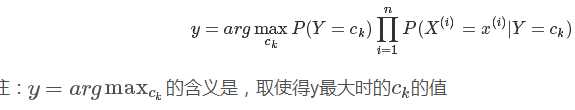
基本步骤:

3、似然函数和概率函数
概率研究的问题是,已知一个模型和参数,怎么去预测这个模型产生的结果的特性(例如均值,方差,协方差等等)。统计是,有一堆数据,要利用这堆数据去预测模型和参数。
概率是已知模型和参数,推数据。统计是已知数据,推模型和参数。
在统计里面,似然函数和概率函数却是两个不同的概念(其实也很相近就是了)。
对于这个函数:P(x|θ)。输入有两个:x表示某一个具体的数据;θ表示模型的参数。
如果θ是已知确定的,x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点x,其出现概率是多少。
如果x是已知确定的,θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现x这个样本点的概率是多少。
4、最大后验概率估计(MAP)
最大似然估计是求参数θ, 使似然函数P(x0|θ)最大。
最大后验概率估计则是想求θ使P(x0|θ)P(θ)最大。求得的θ不单单让似然函数大,θ自己出现的先验概率也得大。
最大后验概率估计是最大似然和贝叶斯估计的结合,

其实如果MAP的后验概率中P(θ) = 1,就是最大似然概率。也就是说最大似然概率默认未知参数 θ 取值都是等可能性的,而最大后验概率在参数估计时考虑了参数的先验概率。
4、对比总结
- 极大似然估计、最大后验估计和贝叶斯估计都是参数估计方法。
- 极大似然估计和最大后验估计都是点估计,即把参数看成未知常数,通过最大化似然和后验概率实现。
- 贝叶斯估计把参数看成一个随机变量,属于分布估计,然后求该随机变量在数据集D下的条件期望。
- 当先验为均匀分布时,极大似然估计和最大后验估计是等价的。即估计参数的先验概率为 1 ;
- 当先验和似然都是高斯分布时,最大后验估计和贝叶斯估计是等价的。
- 通常情况下,贝叶斯估计的积分很难计算,但可以采取一些近似方法,如拉普拉斯和变分近似以及马尔科夫链蒙特卡洛抽样。
参考:https://blog.csdn.net/u011508640/article/details/72815981
以上是关于贝叶斯分类器(2)极大似然估计、MLE与MAP的主要内容,如果未能解决你的问题,请参考以下文章
频率学派 极大似然估计MLE,贝叶斯学派 最大后验估计MAP 2021-05-11
机器学习(二十五)— 极大似然估计贝叶斯估计最大后验概率估计区别
详解最大似然估计(MLE)最大后验概率估计(MAP),以及贝叶斯公式的理解(转)