对于DFT频谱泄漏问题的研究

Posted 2020-10-31 Geek-wireless

问题简介：
对于频率为fs的正弦序列，它的频谱应该只是在fs处有离散谱。但是，在实际利用DFT求它的频谱时，对时域做了截断，结果使信号的频谱不只是在fs处有离散谱，而是在以fs为中心的频带范围内都有谱线出现，它们可以理解为是从fs频率上“泄漏”出去的，这种现象称 为频谱“泄漏”。
不发生泄露的条件：F_c=(mF_s)/N (m为整数，F_c为信号频率，F_s为采样频率)

现象分析：
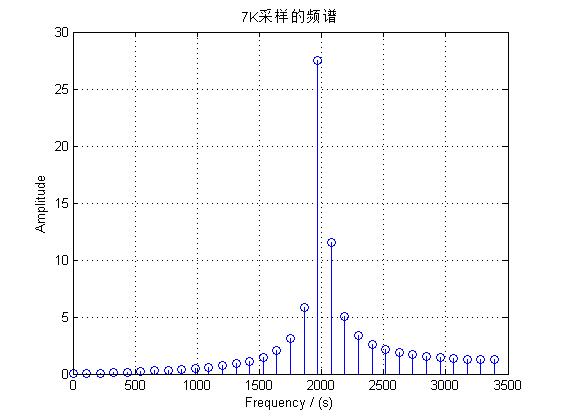
以7K采样为例：
DFT本质是以一个离散的窗函数对信号进行取样，也就是在时域相乘的过程。时域相乘又等价于频域的卷积，并对频域的幅值产生影响，在这里只需要讨论频谱形态而不必讨论幅值，由于本次采样周期为500点，我们画出一个500点矩形序列的频谱图

 

可以看出每个频域的每个小峰宽度都为14Hz，理论上说他们的间隔应为
Fs/N=7000/500=14
与理论相符合

下一步是与信号的频谱进行卷积，由于原信号的理论频谱为在F_c及〖-F〗_c的冲激信号，我们只要将目前的频谱向左向右移动F_c即可，为了方便，只研究右半块。

 

时域采样率为F_s那么在频域中就以F_s/N=7000/500=14Hz，从零点开始等间隔取样，而调制过的信号每个小峰的宽度也为F_s/N=7000/500=14Hz，主峰的宽度为小峰宽度的两倍，也就是28Hz，此时在主峰中会以357*14=4998Hz及358*14=5012Hz进行采样，并且在小峰中也会在峰体中采样，从而显出原信号不存在的频率。

小峰宽度与频域采样宽度相等这就表明每个频域取样点可以正好落在每个小峰的零点上，而落在最高峰的中间，完美显示出原信号的频谱分布，此时采样信号频率应满足：
F_c=(mF_s)/N (m为整数)
如果采样频率不满足这一公式，那么频率域采样点就会处于各个旁瓣中，从而在频域中表现出原信号不存在的频率，这些旁瓣的幅值与原信号频率距离成反比，越靠近信号频率造成的谐波振幅越大。

改进措施
增大FFT变换的点数N。 通过增大N，一方面提高频域分辨率，更大可能满足F=m*Fs/N， 另一方面，压缩采样信号的瓣宽，降低泄露水平。
下图为以不同采样点数得出的频谱：

可以明显看出500点采样比64点采样效果好很多。

 

选用合适的窗函数。根据不同的需求来选择不同特性的窗函数，主瓣宽但旁瓣衰减大的窗或是主瓣窄但旁瓣相对衰减小的窗。

选取7K， 64点采样的频域信号进行测试，选取常用的Hanning窗：

可以看出虽然加窗可以很好地抑制旁瓣，但对于主瓣的频率却不能很好地优化，我也试了一下其他的加窗函数，都不太理想，对于本题测试的窄带信号，主瓣的信号尤为重要，只能采用增加取样点的方法来凸显主瓣信号。、

 

总结

1. 要注意理论与实际的差异，并善于思考其中的原因
2. 善于运用优质网络资源

 

参考文档：https://www.ni.com/white-paper/4844/zhs/

附c++采样程序：

#include<stdio.h>

#include<math.h>

#include<iostream>

#include<fstream>

using namespace std;

void main()

{

    double Fs_7 =7,Fs_10=10,Fs_11=11;//K

    int i;

    int const dn = 10;//延时滤波器长度

    int const s_n =500 ; //序列长度

    double xn[500];

 

    for (i = 0; i<s_n; i++)

    {

         xn[i] =sin(2 * 3.1416 * 5 / Fs_7 * i);

    }

    ofstream SaveFile_a("xn_7.txt");

    for (i = 0; i<s_n; i++)

         SaveFile_a << " " << xn[i] << endl;

    SaveFile_a.close();

 

    for (i = 0; i<s_n; i++)

    {

         xn[i] = sin(2 * 3.1416 * 5 / Fs_10 * i);

    }

    ofstream SaveFile_a1("xn_10.txt");

    for (i = 0; i<s_n; i++)

         SaveFile_a1 << " " << xn[i] << endl;

    SaveFile_a1.close();

 

    for (i = 0; i<s_n; i++)

    {

         xn[i] = sin(2 * 3.1416 * 5 / Fs_11 * i);

    }

    ofstream SaveFile_a1("xn_11.txt");

    for (i = 0; i<s_n; i++)

         SaveFile_a1 << " " << xn[i] << endl;

    SaveFile_a1.close();

}

 

Matlab程序

显示采样过信号的频谱：

xn_f=fopen(\'xn_7.txt\',\'r\');

[xn,count]=fscanf(xn_f,\'%f\');

fclose(xn_f);

 

Fs=7000;

x=xn;

x=x.*hamming(64);%加窗

x = x(:,1);

x = x\';

N = length(x);%

t = (0:N-1)/Fs;%

y = fft(x);

f = Fs/N*(0:round(N/2)-1);

stem(f,abs(y(1:round(N/2))));

xlabel(\'Frequency / (s)\');ylabel(\'Amplitude\');

title(\'7K²ÉÑùµÄƵÆ×\');

grid;

 

显示采样矩形序列频谱：

Fs=7000;

x=boxcar(500);%生成矩形序列

x = x(:,1);

x = x\';

N = length(x);

 

y = fft(x,1000);

y=circshift(y,143,2);

y=abs(y)/10;

f1 = Fs/length(y)*(0:length(y)-1);

plot(f1,y);

xlabel(\'Frequency / (s)\');ylabel(\'Amplitude\');

title(\'ÐźŵÄƵÆ×\');

grid;