快速傅里叶变换FFT C语言实现 可用于嵌入式系统进行模拟采样频谱分析

Posted 2022-11-23 XiaoMing_sususu

快速傅里叶变换C语言实现 模拟采样进行频谱分析

FFT是DFT的快速算法用于分析确定信号(时间连续可积信号、不一定是周期信号)的频率(或相位、此处不研究相位)成分，且傅里叶变换对应的$\omega$是连续的，从而达到分析信号成分的目的。
具体理论参考FFT百度百科原理。
下面给出代码分析以及模拟采样频谱分析的结果。

对于复信号FFT：

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
# define PI	3.14159265358979323846264338327950288 //根据运算精度或要求自行截取位数
#define q	 8
#define N	(1<<q)		   /*2的q次方点数 */
#define Fs  2560           //采样率 Fs > 2fh
typedef float real;
typedef struct
    real Re;
    real Im;
complex;
static void Asm_Mag(complex *x,int n) 

    int i;
    real Mag;
    for(i=0; i<n/2; i++)
    
        Mag = sqrt(x[i].Re*x[i].Re + x[i].Im*x[i].Im)/N;
        printf("第%d个点：%.3f hz 幅度：%.3f \\n",i,(float)i*Fs/N,Mag);
    

void fft( complex *v, int n, complex *tmp )

  if(n>1) 
    int k,m;    complex z, w, *vo, *ve;
    ve = tmp; vo = tmp+n/2;
    for(k=0; k<n/2; k++) 
      ve[k] = v[2*k];
      vo[k] = v[2*k+1];
    
    fft( ve, n/2, v );		/* FFT 偶序列 */
    fft( vo, n/2, v );		/* FFT 奇序列*/
    for(m=0; m<n/2; m++) 
      w.Re = cos(2*PI*m/(double)n);
      w.Im = -sin(2*PI*m/(double)n);
      z.Re = w.Re*vo[m].Re - w.Im*vo[m].Im;
      z.Im = w.Re*vo[m].Im + w.Im*vo[m].Re;
      v[  m  ].Re = ve[m].Re + z.Re;
      v[  m  ].Im = ve[m].Im + z.Im;
      v[m+n/2].Re = ve[m].Re - z.Re;
      v[m+n/2].Im = ve[m].Im - z.Im;
    
  
  return;

int main(void)

      complex v[N],scratch[N];
      int k;
  /* 模拟数字采样 */
    for(k=0; k<N; k++)   //F0= Fs/N、f = w/2*pi、
    v[k].Re =  9999 + 570*cos(690*2*PI*k/(double)Fs);
    v[k].Im =  570*sin(690*2*PI*k/(double)Fs); /* 复数信号分为实部虚部 但一般采样为纯实 虚部为0*/
  
  /* FFT: */
      fft( v, N, scratch );
      Asm_Mag(v,N); //幅度测量

Fs:

其中Fs是采样率，根据奈奎斯特采样定律，当采样频率Fs大于信号中最高频率fs的2倍时(Fs>2fh)，采样之后的数字信号完整地保留了原始信号中的信息，此时进行快速傅里叶变换即可得到信号的全部频率信息。

N:

做快速傅里叶变换FFT的点数必须是2的幂次方。

Fh:

对连续时间信号进行采样过程中，cos/sin($\omega$t)其中t被替换为kTs,即t=kTs.Ts = 1 /Fs;所以代码中的被测信号频率再由$\omega$=2*Pi * f可得 f = $\omega$ / 2 *pi; 此时代码中的被测信号频率为690hz，且幅度为570，而且包含着 9999的直流分量(0hz)。

Fo:

Fo为频谱分辨率，Fo = Fs / N ;此代码例子中为 2560 /256 = 10 hz;这个指标需根据现实题目要求进行调整，且涉及了Fs和N 这三个量可以灵活计算组合。

complex：

FFT目标为复信号，虚部在实际采样或者模拟采样时虚部可以为0，且一般为0。

此FFT是时域抽选方法：DIT2 F先在时域先进行奇欧倒序，频域输出为正序。

结果分析：

结果明显在0hz直流分量有幅度为9999

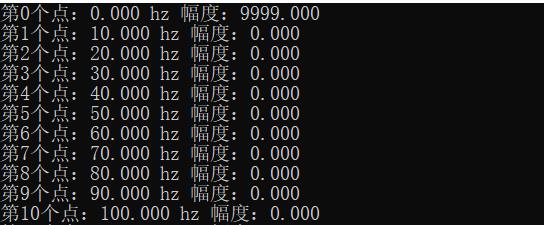
在690hz有幅度570的分量:

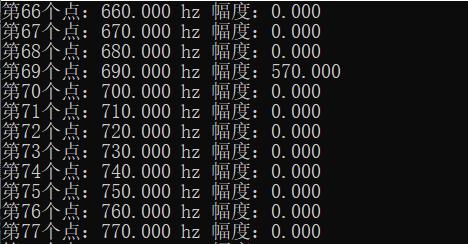
在其余频率分量处并无分幅度。得到了被测信号的全部频率幅度信息。
由于FFT的频谱结果是关于奈奎斯特频率对称的，所以只计算一半的点即可。
其他被测信号可自行模拟测试验证。

对于纯实信号FFT：

此时真实幅度、代码计算应该修改为：

sqrt(x[i].Re*x[i].Re + x[i].Im*x[i].Im)*2/N;(改为纯实数时,需改为2倍)
  if(i==0)
   Mag = Mag /2;    //直流分量不需要乘以2，所以按照乘以2计算后，要除以2

被测信号：

    v[k].Re =  19999 + 570*cos(690*2*PI*k/(double)Fs) + 670*cos(590*2*PI*k/(double)Fs);.//直流分量19999 690hz分量570 590hz分量670
    v[k].Im = 0; //虚部为0

为什么用cos可以思考随机信号分析内容、sin 、cos进行FFT结果一样

纯实信号FFT结果：

可见直流分量0hz幅度为19999

在590hz和690hz均有幅度670 和570

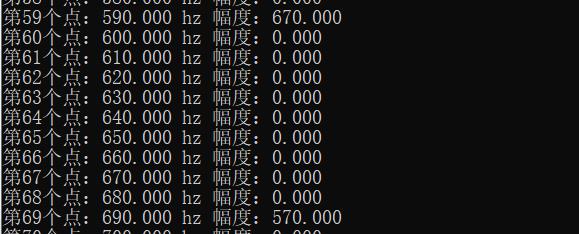
其余频率分量并无幅度，但在真实采样中全频率具有高斯白噪声。