Machine learning for improved image-based wavefront sensing

Posted 2020-10-30 xiaomangxie

---恢复内容开始---

　　基于图像的波前传感是一种利用参数化物理模型和非线性优化计算点扩散函数(Psf)来测量波前误差的方法。当执行基于图像的波前传感时，探测器上捕获一个psf，物理模型创建一个波前，生成一个模拟psf，与优化后的数据相匹配。一个很好的策略是用多项式(如Zernike多项式)对波前进行参数化，从而降低维数，并强制物理上适合于平滑变化的波前。为了确定这些多项式的系数来重建波前，可以采用基于梯度的非线性优化方法来调整系数值。为了确定这些多项式的系数来重建波前，可以采用基于梯度的非线性优化方法来调整系数值。基于梯度的优化器使用从成本函数的梯度计算出的搜索方向将成本函数相对于未知参数集的代价函数最小化。在本文中，代价函数是一个增益和偏差不变的归一化均方误差(Nmse)度量。基于梯度的优化器将调整多项式基的系数，直到误差度量值或梯度值的变化足够小为止。

　　非线性优化算法可以停滞在局部极小，梯度为零。在局部极小的情况下，计算的psf与数据不一致，除了极少数的模糊情况外，它是局部最小的。为了避免局部极小的停滞，在波前误差较大时，需要附加信息，如离焦平面或光滑性知识，或对多项式系数进行良好的起始估计。当初始猜测与真实解不够接近时，在局部极小处停滞的可能性称为“捕获范围问题”，而起始估计与真正解的距离足够接近收敛的距离称为“捕获范围”。可以通过估计均方根波前误差(Rms Wfe)和使用与rms wfe相同数量的多个随机开始猜测来执行全局优化，以便随机选择一个足够接近捕获范围内的真正解的起始估计值。

　　为了在给定的psf捕获范围内生成初始估计值，我们转向机器学习和神经网络。神经网络以前曾被应用于相位恢复，试图恢复Zernike系数。那次尝试使用一个网络，将psf的每个像素作为输入向量的一部分，这是矩阵乘以一个单一的“隐藏”向量，然后通过非线性乙状函数和矩阵乘以泽尼克多项式系数对应的输出向量。 　　

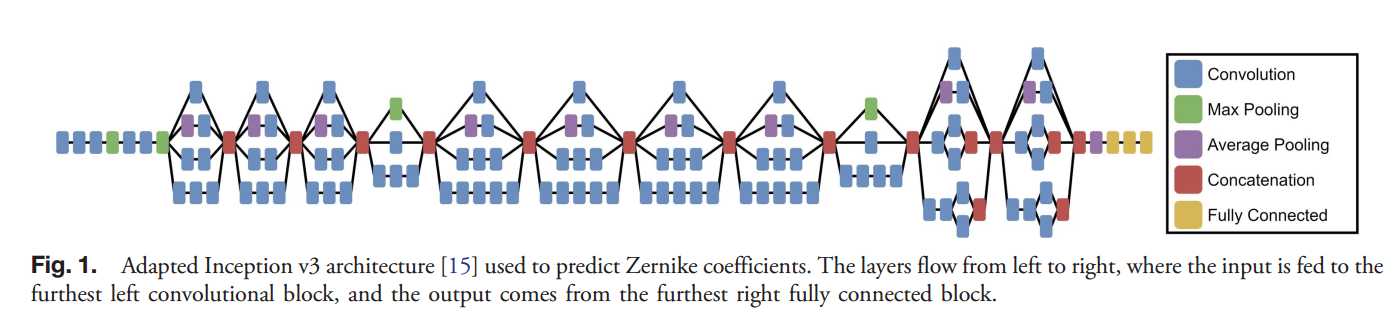
 由于我们已经使用物理模型来描述光在强度平面上的传播和探测，我们可以简单地根据Zernike系数创建模拟psfs并将其输入CNN。这种方法假设我们的模型中有已知的值，如瞳孔振幅、f数和像素间距。对于我们的情况，我们考虑一个均匀照明的JWST孔径，如图所示。它是阵列中的零填充，是光圈宽度的两倍，从而产生一幅nquist采样的psf(图像)。我们基于二阶至五阶全局Zernike多项式产生psfs，不包括任何每段误差。在输入cnn之前，所有psfs都被标准化为最大值为1。我们用minibatch训练与16 PSFS minibatch大小。cnn的学习参数通过每次CNN操作使用反向传播梯度来更新。小批训练根据来自一小批输入的梯度更新CNN的参数，而不仅仅是单个输入，这提高了收敛速度[18]。机器学习依赖随机梯度下降算法，其中更新是基于梯度和一个称为学习速率的参数。学习速率控制更新的步长，较小的学习速率表示在参数空间中的较小移动。为了最小化，我们使用adam，一种基于梯度的随机优化算法，具有自适应的学习速率，这意味着它被初始化为用户定义的值，然后根据用户定义的值进行更新。

我们最初仅用2.3RMS像差波(相当大的像差)训练了5000个周期的psfs模型，初始学习速率为2×10?2，每1000个周期减少一半。然后我们允许公司有任何地方从1到4的RMS波像差RMS波和培训20000时代，开始学习率在1×10?3和降低0.5×10?3后的第一个10000期。最后，我们包括在我们公司，包括泊松噪声和任选包括探测器的噪声，背景噪声，和坏点。一个minibatch这些输入方式的一个例子，图3中可以看出。从均匀分布的随机分布中选取峰值光子和任何附加噪声参数，表1给出了低值和高值。

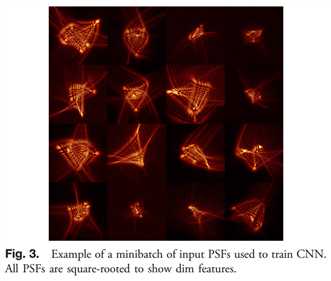
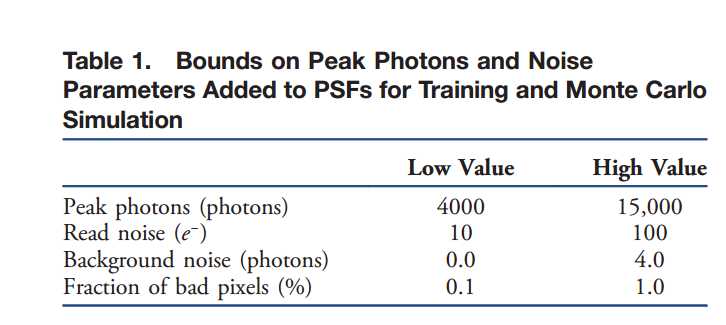
这些噪声的选择使我们的cnn对实验中可以发现的各种各样的噪声都有很强的鲁棒性，我们在这些噪声的psfs上训练了50，000次，从2.5×10?3的学习速率开始，在每10，000次后分别降至1.0×10?3，0.75×10?3，0.5×10?3和0.3×10?3。训练结束后，我们的验证损失为预测和真实Zernike系数之间的0.373波均方根差值，剩余RMSWFE在训练区域内单调增长，如图所示。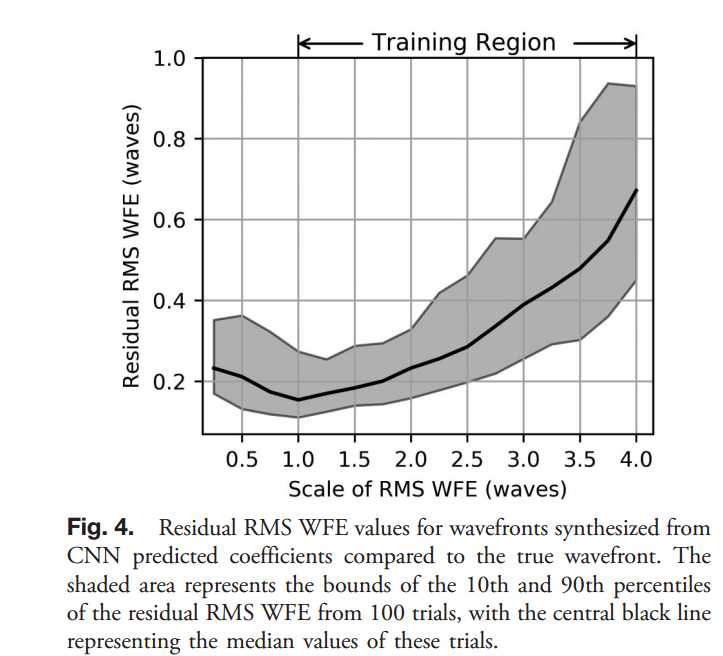

 

 为了确定CNN预测的有效性，我们使用了蒙特卡罗分析。我们模拟的psfs仅由cnn预测的Zernike系数组成。这些模拟的psfs中的噪声产生的方式与训练psfs相同。我们使用了从0.25波到4.0波不等的RMS WFE值，以0.25波为增量。对于每数量的RMS WFE，我们模拟了250种不同的psfs。他的结果是，在我们模拟的检测器窗口内有一些匹配是正确的，但与上述窗口外的真实psf不同。我们将图像阵列的大小增加到512×512像素，因为jwst上的检测器至少是1024×1024像素(23，24)。为了防止出现错误，我们将瞳孔域的采样增加了一倍。我们知道这是合理的，因为jwst上的检测器至少是1024×1024像素[23，24]。还将psf缩小到256×256像素，然后再输入cnn。这意味着我们不需要再训练CNN，可以使用更大的数组进行优化。这些步骤改进了我们分析中的收敛性。