学习笔记：矩阵

Posted 2020-10-29 refun

今天讲了矩阵……就总结一下好了

http://blog.csdn.net/tomorrowtodie/article/details/52311373

http://www.matrix67.com/blog/archives/276 矩阵经典例题

很多内容来自学姐课件

矩阵

啥是矩阵？这个很好懂吧？

（不懂我也没办法）

大体就长这样

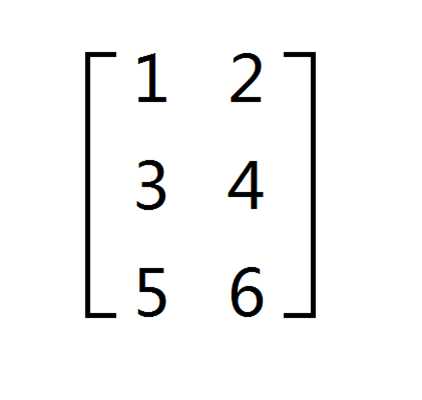
矩阵乘法

蛤？两个矩阵怎么做乘法？并不是所有矩阵都能做乘法的。

只有n行p列的矩阵和p行m列的矩阵才可以相乘。

相乘完就是一个n*m的矩阵喽。

 

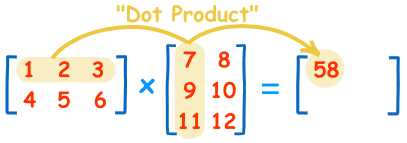
就这样子。左边的每一行分别去和右边的每一列相乘，然后取和

比如取了左边的第二行和右边的第一列相乘

那么他们的和就应该放在结果的第二行第一列上。

代码如下：

1 for (int i=1;i<=n;++i)
2     for (int j=1;j<=m;++j)
3         for (int k=1;k<=p;++k)
4             c[i][j]+=a[i][k]*b[k][j];

代码是不是看起来很水？理解了就很好懂了……

WARNING!

矩阵乘法不满足交换律！即A*B!=B*A

但矩阵乘法满足结合律！即A*B*C=A*(B*C)

 

矩阵乘法的应用

恩……说了这么多矩阵乘法究竟该怎么用呢？

FIRST 矩阵乘法优化DP

这可能是矩阵乘法用的最多的地方了吧……

 

举个栗子

求Fibonacci数列第n项的值

n<=10¹⁸

 

数据这么大要是一步步安稳递推我们怕不是要TLE到飞起

那就走个捷径好了

快速幂！

……

哎等等不是应该用矩阵乘法吗

如图

 

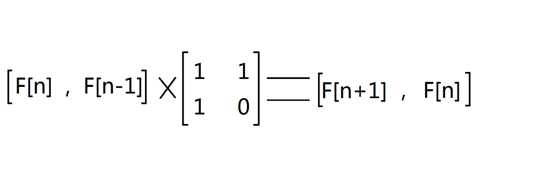
哎这样是不是就能做了？

先给上式中第二个矩阵命名为P，给矩阵[F[2],F[1]]命名为A

那么[F[3],F[2]]就可以用矩阵A*P计算得出。同理

若求F[10]就可以A*P⁸，而P⁸我们就可以用快速幂求了

复杂度为log级别。模板如下：

 1 struct Mar
 2 {
 3     int a[N][N];
 4 } unit, A,ans;
 5 //PS这里的unit为单位矩阵，即左上角到右下角对角线为1的矩阵，它有一个性质，即为任何矩阵乘上单位矩阵都为本身
 6 Mar Mul(Mar a, Mar b)//矩阵乘法
 7 {
 8     Mar ans;
 9     memset(ans.a,0,sizeof(ans.a));
10     for (int k=1; k<=n; ++k)
11         for (int i=1; i<=n; ++i)
12             for (int j=1; j<=n; ++j)
13                 ans.a[i][j]=(ans.a[i][j]+a.a[i][k]*b.a[k][j])%Mod;
14     return ans;
15 }
16 Mar Qpow(Mar a,int p)//矩阵快速幂
17 {
18     Mar ans=unit;//相当于快速幂中的初始化为1
19     while (p!=0)
20     {
21         if (p&1)
22             ans=Mul(ans,a);
23         a=Mul(a,a);
24         p>>=1;
25     }
26     return ans;
27 }

 

练习

已知递推式F(n)=2*F(n-1)+3*F(n-2)，求F(n)

已知递推式F(n)=F(n-1)+3*F(n-2)+4*F(n-4)，求F(n)

已知递推式F(n)=sigma(i=1..10)a[i]*F(n-i)，读入a[i]数组，求F(n)

BZOJ1898 沼泽鳄鱼

(核心：12为一个周期)

 

SECOND 图的邻接矩阵+矩阵乘法

？？？？

这是个啥玩意儿？

构造无向图的邻接矩阵G

G*G以后得到一个什么东西？ (GG)

可发现

如果(i,j)=1并且(j,k)=1

那么G*G的(i,k)+=1

经过了两条边！

G^k 即为经过了k条边，

可以扩展到有向图

若想要可以在一个点停留

 

如果不允许走回头路呢？

对于一个无向图，我们可以将边变为点，若从能点a经过边i到b，再从点b经过边j到c，那么就化边为点，设i，j两边可以相互抵达，用邻接矩阵存即可，类似上面的不能在一个点停留。

例：BZOJ1875 HH去散步

 

矩乘DP的特点？

一般看到那种某个限制的范围非常小的就可以考虑一下矩乘

但是也有可能是状压

如果一个限制非常小，一个限制非常大，那基本上就是矩乘了

long long 太慢了！

少取模！