学习笔记：树链剖分

Posted 2020-10-29 refun

现在的noip好像难度一年比一年高了啊……去年（2016）的noip竟然考了一道链剖……如果我当时在考场上怕不是要直接GG……所以吓得我赶紧来学链剖了（虽然学了估计我考场上也写不出）。

什么是树链剖分？

树链剖分……如果你不会线段树的话……还是就此打住吧。

树链剖分，顾名思义，就是将一颗树分解成一条条链（废话）

然后将这一条条链收尾相接连成一条链，用线段树进行查询和修改

通常用来处理在一颗形状恒不变的树上，修改边/点权，查询某个值的题目。

没了……（词穷）

如何实现树链剖分？

先引入几个概念

首先定义：

Weight[u]保存u节点的子树大小

Father[u]保存u节点的父亲节点

Son[u]表示u节点的重儿子节点

Top[u]表示u节点的重链的顶端节点

T_NUM[u]表示u与其父亲的连边在线段树中的编号

TREE[u]线段树区间中下标为u的点权

也许到这就看不懂了？没事，抱着疑问继续往下看

重儿子：Weight[u]为 若v为u的的子节点中子树最大的，那么v就是u的重儿子。

轻儿子：v的其它子节点。
重边：点v与其重儿子的连边。
轻边：点v与其轻儿子的连边。
重链：由重边连成的路径。
轻链：轻边。

……

……

……

……

……

……

……

……

……

算了我好像都没给自己说懂……我还是举个例子吧

 

举个栗子

下图中粗的为重链（如1-4-9-13-14），细的为轻链，带红点的为重链的顶端结点(Top)，每个边表示了它在线段树区间的坐标(T_NUM)，下标为T_NUM[x]的线段树区间存x的点/边权

 

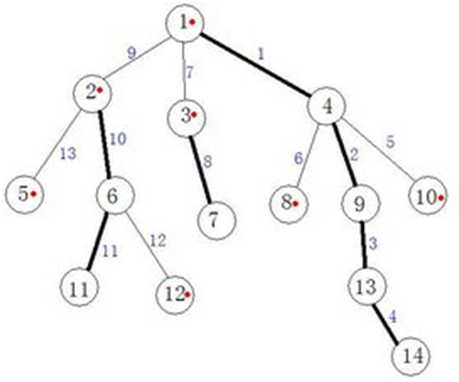
到这应该数组概念都懂了吧？

唯一的疑惑是，T_NUM是按怎么算的？这里为了保证重链区间的连续性，所以我们dfs遍历的时候优先走重链，那样就可以保证重链在线段树区间中是一段连续的区间啦。

 

修改

不妨想想，我们为什么要用线段树呢？

因为线段树可以很方便的对区间（点）进行修改和查询！

所以如果修改点的话……这玩意儿直接修改就好了啊……

但修改区间呢？这个和下面的查询是类似的，不过查询是一边跳一边query，修改是一边跳一边update……往下看就知道了

别告诉我你不会线段树……开头我提醒过的emm……

（不会的你还是去面壁吧……）

 

查询

1.查询路径

我们不妨先考虑如果暴力在一颗动态的树上查询，我们应该怎么做？

当然是找LCA然后一步步查询了！不过一步步往上跳显然太慢了。

所以轻重链的作用其实就是为了让我们跳的更快！

如何跳的更快呢？

我们模仿LCA，当两个点不在同一条重链上时，每次让两个点中Top更深的往上跳，如果当前要跳的点在重链上的话，恭喜你，你的点可以直接跳到这条重链的顶端了！中途的过程我们就用线段树的区间查询好了。毕竟建线段树的时候我们保证了重链上的点在线段树的区间中是连续的。

直到两个点跳到同一条重链上。我们再模仿LCA最后一起跳一步的方法，最后我们只需要查询两个点在当前重链之间的信息就好了。

这样就可以快很多了。

例如：

当要修改11到10的路径时。
    第一次迭代：u = 11，v = 10，f1 = 2，f2 = 10。此时dep[f1] < dep[f2]，因此     修改线段树中的5号点，v = 4, f2 = 1；
    第二次迭代：dep[f1] > dep[f2]，修改线段树中10--11号点。u = 2，f1 = 2；
    第三次迭代：dep[f1] > dep[f2]，修改线段树中9号点。u = 1，f1 = 1；
    第四次迭代：f1 = f2且u = v，修改结束。

2.查询子树（补）

这个其实很简单的……观察上面的图我们可以发现某个节点的子树中的每个点/边在线段树区间中一定是连续的……所以我们直接区间查询就好了……修改也是同理……

 

不多说了，贴代码（单点修改，查询路径最大值或长度BZOJ1036）

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstdlib>
  4 #include<cstring>
  5 using namespace std;
  6 
  7 int head[30001],num_edge;
  8 int Father[30001],Weight[30001];
  9 int Son[30001],Top[30001];
 10 int T_NUM[30001],a[30001];
 11 int Depth[30001]; 
 12 int sum,n,INF,ans;
 13 int TREE[30001];
 14 string st;
 15 struct node
 16 {
 17     int to,next;
 18 } edge[60005];
 19 struct node1
 20 {
 21     int max,sum;
 22 }Segt[120001];
 23 void add(int u,int v)
 24 {
 25     edge[++num_edge].to=v;
 26     edge[num_edge].next=head[u];
 27     head[u]=num_edge;
 28 }
 29 void dfs1(int x)//第一遍bfs处理Son,Weight,Depth几个数组
 30 {
 31     Weight[x]=1;
 32     Depth[x]=Depth[Father[x]]+1;
 33     for (int i=head[x]; i!=0; i=edge[i].next)
 34         if (edge[i].to!=Father[x])
 35         {
 36             Father[edge[i].to]=x;
 37             dfs1(edge[i].to);
 38             Weight[x]+=Weight[edge[i].to];
 39             if (Son[x]==0 || Weight[edge[i].to]>Weight[Son[x]])
 40                 Son[x]=edge[i].to;
 41         }
 42 }
 43 
 44 void dfs2(int x,int tp)//第二次就优先dfs重儿子，建立线段树
 45 {
 46     T_NUM[x]=++sum;
 47     TREE[sum]=a[x];
 48     Top[x]=tp;
 49     if (Son[x]!=0)
 50         dfs2(Son[x],tp);
 51     for (int i=head[x]; i!=0; i=edge[i].next)
 52         if (edge[i].to!=Son[x] && edge[i].to!=Father[x])
 53             dfs2(edge[i].to,edge[i].to);
 54 }
 55 
 56 void Build(int node,int l,int r,int a[])//这个和下面的Update都是线段树板子……
 57 {
 58     if (l==r)
 59         Segt[node].max=Segt[node].sum=a[l];
 60     else
 61     {
 62         int mid=(l+r)/2;
 63         Build(node*2,l,mid,a);
 64         Build(node*2+1,mid+1,r,a);
 65         Segt[node].max=max(Segt[node*2].max,Segt[node*2+1].max);
 66         Segt[node].sum=Segt[node*2].sum+Segt[node*2+1].sum;
 67     }
 68 }
 69 
 70 void Update(int node,int l,int r,int x,int k)
 71 {
 72     if (l==r)
 73         Segt[node].max=Segt[node].sum=k;
 74     else
 75     {
 76         int mid=(l+r)/2;
 77         if (x<=mid)
 78             Update(node*2,l,mid,x,k);
 79         else
 80             Update(node*2+1,mid+1,r,x,k);
 81         Segt[node].max=max(Segt[node*2].max,Segt[node*2+1].max);
 82         Segt[node].sum=Segt[node*2].sum+Segt[node*2+1].sum;
 83     }
 84 }
 85 
 86 int QueryMax(int node,int l,int r,int l1,int r1)//查询区间最大值，线段树模板
 87 {
 88     if (r<l1 || l>r1)
 89         return -INF;
 90     if (l1<=l && r<=r1)
 91         return Segt[node].max;
 92     int mid=(l+r)/2;
 93     return max(QueryMax(node*2,l,mid,l1,r1),
 94                QueryMax(node*2+1,mid+1,r,l1,r1));
 95 }
 96 
 97 int QuerySum(int node,int l,int r,int l1,int r1)//查询区间和，线段树模板
 98 {
 99     if (r<l1 || l>r1)
100         return 0;
101     if (l1<=l && r<=r1)
102         return Segt[node].sum;
103     int mid=(l+r)/2;
104     return QuerySum(node*2,l,mid,l1,r1)+
105            QuerySum(node*2+1,mid+1,r,l1,r1);
106 }
107 
108 int GetSum(int x,int y)//求x和y点之间的路径长度和
109 {
110     int fx,fy;
111     memset(&ans,0,sizeof(ans));
112     fx=Top[x];fy=Top[y];
113     while (fx!=fy)
114     {
115         if (Depth[fx]<Depth[fy])
116             swap(fx,fy),swap(x,y);
117         ans+=QuerySum(1,1,n,T_NUM[fx],T_NUM[x]);
118         x=Father[fx],fx=Top[x];
119     }
120     if (Depth[x]>Depth[y]) swap(x,y);
121     return ans+=QuerySum(1,1,n,T_NUM[x],T_NUM[y]);
122 }
123 
124 int GetMax(int x,int y//求x和y点之间的最大一条路径长度
125 {
126     int fy,fx;
127     memset(&ans,-0x7f,sizeof(ans));
128     fx=Top[x];fy=Top[y];
129     while (fx!=fy)
130     {
131         if (Depth[fx]<Depth[fy])
132             swap(fx,fy),swap(x,y);
133         ans=max(ans,QueryMax(1,1,n,T_NUM[fx],T_NUM[x]));
134         x=Father[fx],fx=Top[x];
135     }
136     if (Depth[x]>Depth[y]) swap(x,y);
137     return max(ans,QueryMax(1,1,n,T_NUM[x],T_NUM[y]));
138 }
139 
140 int main()
141 {
142     ios::sync_with_stdio(false);
143     int i,u,v,l,m,x,y;
144     memset(&INF,0x7f,sizeof(INF));
145     cin>>n;
146     for (i=1; i<=n-1; ++i)
147     {
148         cin>>u>>v;
149         add(u,v);
150         add(v,u);
151     }
152     for (int i=1;i<=n;++i)
153         cin>>a[i];
154     Depth[1]=1;
155     dfs1(1);
156     dfs2(1,1);//两边预处理 
157     Build(1,1,n,TREE);//TREE数组保存用来建线段树的区间 
158     cin>>m;
159     for (int i=1;i<=m;++i)
160     {
161         cin>>st>>x>>y;
162         if (st=="CHANGE")
163             Update(1,1,n,T_NUM[x],y);
164         if (st=="QMAX")
165             cout<<GetMax(x,y)<<endl;
166         if (st=="QSUM")
167             cout<<GetSum(x,y)<<endl;
168     }
169 }