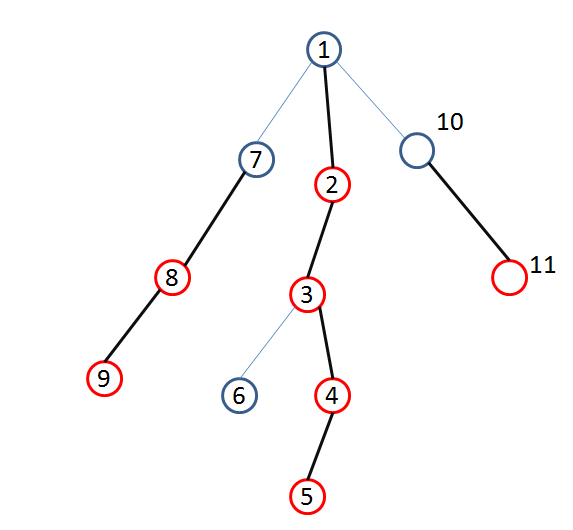
重儿子:子树包含节点最多的儿子就是重儿子,如图:
重链:连接重儿子的边
轻链:其它边

红色节点为重儿子,黑边为重链,蓝边为轻链
结论:可以证明从根节点到任意节点都不会经过\(\log_2^n\)条边
树剖:根据上一个结论,可以把树上问题转换为区间问题,每次处理一条链,最多处理\(\log_2^n\)条链
现在问题是如何转换为区间
根据dfs序,可以知道以x为根的子树便利的顺序是比x要晚的;
所以,可以把树重编号,使得链上的编号是连续的,如上图编完号后:
具体操作是先找出重儿子,在优先搜重儿子,重编号,两边dfs即可:
void dfs1(int x,int f){
size[x]=1;fa[x]=f;
for(int i=head[x];i;i=a[i].last) if(a[i].to!=f){
deep[a[i].to]=deep[x]+1;
dfs1(a[i].to,x);
if(!son[x]||size[son[x]]<size[a[i].to]) son[x]=a[i].to;
size[x]+=size[a[i].to];
}
}
void dfs2(int x,int t){
top[x]=t;id[x]=++js;key[js]=x;
if(!son[x]) return ;
dfs2(son[x],t);
for(QAQ i=head[x];i;i=a[i].last) if(a[i].to!=fa[x]&&a[i].to!=son[x]) dfs2(a[i].to,a[i].to);
}有了这些个区间就可以很方便的进行一些树上问题,比如子树修改,子树查询,链修改,链查询......直接套一个线段树就可以了
至于找区间,用类似LCA的方法,每次去找这两条链最顶端的部分,比较一下,进行区间操作,如果两个点的链顶相同,说明两点在一条链上,跳出后再处理一下就可以了
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y);
do_sth(id[top[x]],id[x]);//对这条链上被包含的区间进行操作
x=fa[top[x]];//跳到链顶
}
if(deep[x]>deep[y]) swap(x,y);
Tree::add(1,n,1,id[x],id[y],z);//最后在处理一下如果树上操作是对于树边的话,把边拽下来放到点上,注意:如果两点相等,不能进行操作,因为一个点不能组成边
先来一道对点进行操作的题:
bzoj4538 [HNOI2016]网络
题目描述
一个简单的网络系统可以被描述成一棵无根树。每个节点为一个服务器。连接服务器与服务器的数据线则看做一条树边。两个服务器进行数据的交互时,数据会经过连接这两个服务器的路径上的所有服务器(包括这两个服务器自身)。
由于这条路径是唯一的,当路径上的某个服务器出现故障,无法正常运行时,数据便无法交互。此外,每个数据交互请求都有一个重要度,越重要的请求显然需要得到越高的优先处理权。现在,你作为一个网络系统的管理员,要监控整个系统的运行状态。系统的运行也是很简单的,在每一个时刻,只有可能出现下列三种事件中的一种:
在某两个服务器之间出现一条新的数据交互请求;
某个数据交互结束请求;
某个服务器出现故障。系统会在任何故障发生后立即修复。也就是在出现故障的时刻之后,这个服务器依然是正常的。但在服务器产生故障时依然会对需要经过该服务器的数据交互请求造成影响。
你的任务是在每次出现故障时,维护未被影响的请求中重要度的最大值。注意,如果一个数据交互请求已经结束,则不将其纳入未被影响的请求范围。
输入输出格式
输入格式:
第一行两个正整数n,m,分别描述服务器和事件个数。服务器编号是从1开始的,因此n个服务器的编号依次是1,2,3,...,n。
接下来n-1行,每行两个正整数u,v,描述一条树边。u和v是服务器的编号。
接下来m行,按发生时刻依次描述每一个事件;即第i行(i=1,2,3,...,m)描述时刻i发生的事件。每行的第一个数type描述事件类型,共3种类型:
(1)若type=0,之后有三个正整数a,b,v,表示服务器a,b之间出现一条重要度为v的数据交互请求;
(2)若type=1,之后有一个正整数t,表示时刻t(也就是第t个发生的事件)出现的数据交互请求结束;
(3)若type=2,之后有一个正整数x,表示服务器x在这一时刻出现了故障。
对于每个type为2的事件,就是一次询问,即询问”当服务器x发生故障时,未被影响的请求中重要度的最大值是多少?“注意可能有某个服务器自身与自身进行数据交互的情况。\(2 \leq n \leq 10^5, 1 \leq m \leq 2\ast 10^5\),其他的所有输入值不超过 \(10^9\)
输出格式:
对于每个type=2的事件,即服务器出现故障的事件,输出一行一个整数,描述未被影响的请求中重要度的最大值。如果此时没有任何请求,或者所有请求均被影响,则输出-1。
输入输出样例
输入样例#1:
13 23
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
6 10
6 11
7 12
7 13
2 1
0 8 13 3
0 9 12 5
2 9
2 8
2 2
0 10 12 1
2 2
1 3
2 7
2 1
0 9 5 6
2 4
2 5
1 7
0 9 12 4
0 10 5 7
2 1
2 4
2 12
1 2
2 5
2 3输出样例#1:
-1
3
5
-1
1
-1
1
1
3
6
7
7
4
6题解:
直接维护经过某个点的请求很麻烦,我们可以维护未经过这个点的最大值;
因为涉及删除操作,直接开两个堆,维护删除的和未被删除的,若删除堆堆顶等于未被删除堆堆顶,直接pop();
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<bitset>
#include<cstdlib>
#define QAQ int
#define TAT long long
#define OwO bool
#define ORZ double
#define F(i,j,n) for(QAQ i=j;i<=n;++i)
#define E(i,j,n) for(QAQ i=j;i>=n;--i)
#define MES(i,j) memset(i,j,sizeof(i))
#define MEC(i,j) memcpy(i,j,sizeof(j))
#define mid (l+r>>1)
#define ls (o<<1)
#define rs (o<<1|1)
#define LS l,mid,ls
#define RS mid+1,r,rs
using namespace std;
const QAQ N=100005;
QAQ n,m;
QAQ top[N],id[N],son[N],size[N],deep[N],fa[N];
struct data{
QAQ to,last;
}a[N<<1];
QAQ head[N],js;
struct ddd{
priority_queue<QAQ> q[2];
QAQ get(){
while(!q[1].empty()&&q[0].top()==q[1].top()) q[0].pop(),q[1].pop();
return q[0].empty() ? -1 : q[0].top();
}
}tree[N<<2];
QAQ qu[N][3];
struct hhh{
QAQ l,r;
friend OwO operator < (const hhh &x,const hhh &y){
return x.l<y.l;
}
}b[N<<1];
void add(QAQ x,QAQ y){
a[++js].to=y;a[js].last=head[x];head[x]=js;
}
void dfs1(QAQ x,QAQ f){
size[x]=1;fa[x]=f;
for(QAQ i=head[x];i;i=a[i].last) if(a[i].to!=f){
deep[a[i].to]=deep[x]+1;
dfs1(a[i].to,x);
if(!son[x]||size[son[x]]<size[a[i].to]) son[x]=a[i].to;
size[x]+=size[a[i].to];
}
}
void dfs2(QAQ x,QAQ t){
top[x]=t;id[x]=++js;
if(!son[x]) return ;
dfs2(son[x],t);
for(QAQ i=head[x];i;i=a[i].last) if(a[i].to!=fa[x]&&a[i].to!=son[x]) dfs2(a[i].to,a[i].to);
}
namespace Tree{
void change(QAQ l,QAQ r,QAQ o,QAQ x,QAQ y,QAQ z,QAQ opt){
if(x>y) return ;
if(l>=x&&r<=y){
tree[o].q[opt].push(z);
return ;
}
if(x<=mid) change(LS,x,y,z,opt);
if(y>mid) change(RS,x,y,z,opt);
}
QAQ query(QAQ l,QAQ r,QAQ o,QAQ p){
if(l==r) return tree[o].get();
if(p<=mid) return max(tree[o].get(),query(LS,p));
return max(tree[o].get(),query(RS,p));
}
}
void change(QAQ x,QAQ y,QAQ z,QAQ opt){
js=0;
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y);
b[++js].l=id[top[x]];b[js].r=id[x];
x=fa[top[x]];
}
if(deep[x]>deep[y]) swap(x,y);
if(x!=y) b[++js].l=id[x],b[js].r=id[y];
sort(b+1,b+js+1);
QAQ l=1;
F(i,1,js){
Tree::change(1,n,1,l,b[i].l-1,z,opt);
l=b[i].r+1;
}
Tree::change(1,n,1,l,n,z,opt);
}
QAQ main(){
scanf("%d%d",&n,&m);
F(i,1,n-1){
QAQ u,v;
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
deep[1]=1;js=0;
dfs1(1,0);dfs2(1,0);
F(i,1,m){
QAQ opt;
scanf("%d",&opt);
if(opt==0){
QAQ u,v,w;
scanf("%d%d%d",&u,&v,&w);
qu[i][0]=u;qu[i][1]=v;qu[i][2]=w;
change(u,v,w,0);
}
else if(opt==1){
QAQ t;
scanf("%d",&t);
change(qu[t][0],qu[t][1],qu[t][2],1);
}
else {
QAQ p;
scanf("%d",&p);
printf("%d\n",Tree::query(1,n,1,id[p]));
}
}
return 0;
}另一道关于边的题:
[USACO11DEC]牧草种植Grass Planting
题意
给出一棵n个节点的树,有m个操作,操作为将一条路径上的边权加一或询问某条边的权值。
\(n\leq 100000,m\leq100000\)
输入输出格式
输入格式:
第一行两个数\(n,m\)
接下来\(n-1\)行,每行两个数\(x,y\),表示\(x,y\)之间有一条边
在接下来\(m\)行,每行一个字符c,两个元素x,y
若c为"P",将x,y之间的路径边权+1;
若c为"Q",输出x,y之间的边权和
输出格式:
对于每个"Q",输出答案
输入输出样例
输入样例#1:
4 6
1 4
2 4
3 4
P 2 3
P 1 3
Q 3 4
P 1 4
Q 2 4
Q 1 4 输出样例#1:
2
1
2 题解
树剖模板,仅仅是示例一下边权转点权
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<bitset>
#include<cstdlib>
#define QAQ int
#define TAT long long
#define OwO bool
#define ORZ double
#define F(i,j,n) for(QAQ i=j;i<=n;++i)
#define E(i,j,n) for(QAQ i=j;i>=n;--i)
#define MES(i,j) memset(i,j,sizeof(i))
#define MEC(i,j) memcpy(i,j,sizeof(j))
#define mid (l+r>>1)
#define ls o<<1
#define rs o<<1|1
#define LS l,mid,ls
#define RS mid+1,r,rs
using namespace std;
const QAQ N=100005;
QAQ n,m;
QAQ id[N],top[N],deep[N];
QAQ fa[N],son[N],size[N];
struct data{
QAQ to,last;
}a[N<<1];
QAQ head[N],js;
struct ddd{
QAQ sum,lazy;
}tree[N<<2];
void Add(QAQ x,QAQ y){
a[++js].to=y;a[js].last=head[x];head[x]=js;
}
void dfs1(QAQ x,QAQ f){
size[x]=1;fa[x]=f;
for(QAQ i=head[x];i;i=a[i].last) if(a[i].to!=f){
deep[a[i].to]=deep[x]+1;
dfs1(a[i].to,x);
if(!son[x]||size[son[x]]<size[a[i].to]) son[x]=a[i].to;
size[x]+=size[a[i].to];
}
}
void dfs2(QAQ x,QAQ t){
id[x]=++js;top[x]=t;
if(!son[x]) return ;
dfs2(son[x],t);
for(QAQ i=head[x];i;i=a[i].last) if(a[i].to!=fa[x]&&a[i].to!=son[x])
dfs2(a[i].to,a[i].to);
}
namespace Tree{
void push_up(QAQ o){
tree[o].sum=tree[ls].sum+tree[rs].sum;
}
void push_down(QAQ o,QAQ l){
if(tree[o].lazy){
tree[ls].sum+=tree[o].lazy*(l-(l>>1));
tree[ls].lazy+=tree[o].lazy;
tree[rs].sum+=tree[o].lazy*(l>>1);
tree[rs].lazy+=tree[o].lazy;
tree[o].lazy=0;
}
}
void add(QAQ l,QAQ r,QAQ o,QAQ x,QAQ y){
if(l>=x&&r<=y){
tree[o].sum+=r-l+1;
tree[o].lazy++;
return ;
}
push_down(o,r-l+1);
if(x<=mid) add(LS,x,y);
if(y>mid) add(RS,x,y);
push_up(o);
}
QAQ query(QAQ l,QAQ r,QAQ o,QAQ x,QAQ y){
if(l>=x&&r<=y) return tree[o].sum;
push_down(o,r-l+1);
QAQ ans=0;
if(x<=mid) ans+=query(LS,x,y);
if(y>mid) ans+=query(RS,x,y);
return ans;
}
}
void add(QAQ x,QAQ y){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y);
Tree::add(1,n,1,id[top[x]],id[x]);
x=fa[top[x]];
}
if(x==y) return ;
if(deep[x]>deep[y]) swap(x,y);
Tree::add(1,n,1,id[x]+1,id[y]);
}
QAQ query(QAQ x,QAQ y){
QAQ ans=0;
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y);
ans+=Tree::query(1,n,1,id[top[x]],id[x]);
x=fa[top[x]];
}
if(x==y) return ans;
if(deep[x]>deep[y]) swap(x,y);
ans+=Tree::query(1,n,1,id[x]+1,id[y]);
}
QAQ main(){
scanf("%d%d",&n,&m);
F(i,1,n-1){
QAQ u,v;
scanf("%d%d",&u,&v);
Add(u,v);Add(v,u);
}
js=0;deep[1]=1;
dfs1(1,0);dfs2(1,0);
while(m--){
char opt;
cin>>opt;
if(opt=='P'){
QAQ l,r;
scanf("%d%d",&l,&r);
add(l,r);
}
else {
QAQ l,r;
scanf("%d%d",&l,&r);
printf("%d\n",query(l,r));
}
}
return 0;
}