树链剖分
一个听起来很高级的数据结构
但其实就是一个比较优雅的暴力
树链剖分
字面意思,就是把树上的路径剖成一条条链
首先是树链剖分的一些定义:
size[u] 包括u在内u的子节点个数
son[u] 结点u的重儿子
dep[u] 结点u的深度
fa[u] 结点u的父亲节点
top[u] 结点u所在重链中深度最小的结点
重儿子:即u的所有儿子中size最大的那个儿子(若有相同则任选一个)
重边:即连接重儿子与其父亲的边
重链:相邻重边连接形成的路径
轻儿子:对于一个节点u,除了其重儿子其他全是轻儿子
对于每个结点u
若u是轻儿子,top[u]=u
若u是重儿子,top[u]可直接由其父亲下传
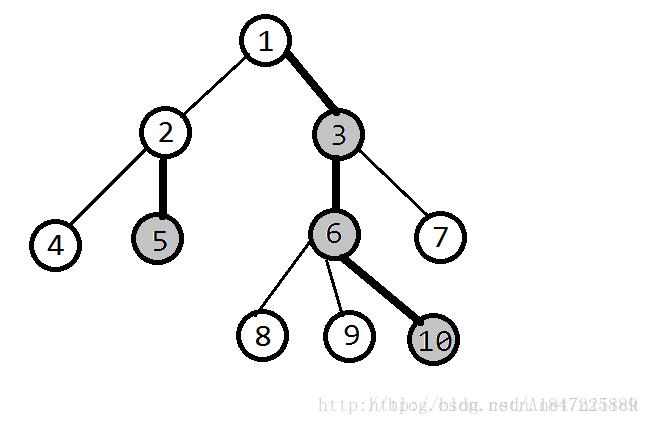
如图中粗变即为重边
1->3->6->10 / 2->5 是重链
top[1]=1; top[2]=2; top[3]=1; top[4]=4;
top[5]=2; top[6]=1; top[7]=7; top[8]=8;
top[9]=9; top[10]=1;
以上可以由两个dfs预处理出
之后便可以将这些链变成连续的区间在线段树上进行修改了
其中num[]记录树上结点对应线段树中的编号
pre[]记录线段树上的编号对应原树上的哪个结点
调用前初始化dep[rt]=1;
调用dfs1(rt,-1);dfs2(rt,rt);
void dfs1(int u,int pa)
{
size[u]=1;//初始化size,表示只有自己
for(int i=head[u];i;i=E[i].nxt)
{
int v=E[i].v;
if(v==pa) continue;
dep[v]=dep[u]+1; fa[v]=u;
dfs1(v,u);
size[u]+=size[v];//另u的size加上其儿子的size
if(size[v]>size[son[u]]) son[u]=v;//判断重儿子
}
}
void dfs2(int u,int tp)
{
num[u]=++cnt; pre[cnt]=u; //记录对应编号
top[u]=tp;//记录链顶
if(son[u]) dfs2(son[u],tp);//如果有重儿子则先处理重儿子
for(int i=head[u];i;i=E[i].nxt)
{
int v=E[i].v;//处理其他轻儿子
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}两道树链剖分的应用模板题题解: