分治法

Posted 2020-10-28 legoxz

乘方问题

输入一个实数x，一个整数n >= 0，计算xⁿ。

朴素算法即时对n个x连乘。

分治法：

　　xⁿ = x^n/2 · x^n/2           如果n为偶数

　　xⁿ = x^(n-1)/2 · x^(n+1)/2    如果n为奇数

T(n) = T(n/2) + θ(1) = θ(lg n)

#include<stdio.h>

double Power_Divide(double x, int n);

int main()
{
    int n;
    double x;
    scanf("%d%lf", &n, &x);
    printf("%.3f", Power_Divide(x, n));
    return 0;
}

double Power_Divide(double x, int n)
{
    if(n == 1)
        return x;
    else if(n % 2 == 0)
        return Power_Divide(x, n / 2) * Power_Divide(x, n / 2);
    else if(n % 2 != 0)
        return Power_Divide(x, (n + 1) / 2) * Power_Divide(x, (n - 1) / 2);
}

 

 

Bottom-up algorithm

自下而上递归解决的算法

 

在理论上，根据斐波那契数列的性质

可采用朴素平方递归式求第n项的斐波那契数列

F_n = Φⁿ / √5   并取整至最接近的整数。可以用平方递归在 log n 的时间内计算出。

但是在现实的计算中无法实现。

根据斐波那契数列的一个定理：

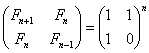通过计算矩阵的n次幂来得到F_n。

这时候是一个log n 的时间算法。