数学中的生物学特性----遗传和变异
说明:此篇博文,是授课偶得,纯属玩笑之举,脱离了数学的严密性,不过从其他学科来解读数学,也不失一乐,读完也许能更深的体会到万事万物都是有关联的。
学习过生物学的人大抵都知道,子代会接受父代的遗传,当然也会有部分的变异。用这一观点我们也能解释数学上的函数问题。
比如,已知函数\\(f(x)=x\\)和函数\\(g(x)=\\cfrac{1}{x}\\),都是我们高中阶段需要熟练掌握的函数之一,那么函数\\(h(x)=x+\\cfrac{1}{x}=f(x)+g(x)\\),所以函数\\(f(x)\\)和\\(g(x)\\)可以看成函数\\(h(x)\\)的父代,函数\\(h(x)\\)可以看成子代。
那么子代函数\\(h(x)\\)和父代函数\\(f(x)\\)与g(x)在图像和性质上有没有关联呢,他们又是如何关联的呢?从生物学的角度解读数学有没有其应用价值?这些问题才是我们需要关注的。
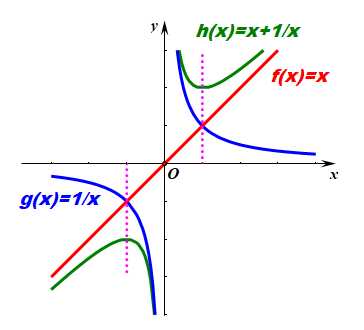
回顾:如图所示的红色为函数\\(f(x)=x\\),定义在\\(R\\)上,奇函数,在\\(R\\)上单调递增,关于点\\((0,0)\\)对称;
蓝色的函数\\(g(x)=\\cfrac{1}{x}\\),定义在\\((-\\infty,0)\\cup (0,+\\infty)\\)上,奇函数,在\\((-\\infty,0)\\)和\\((-\\infty,0)\\)上单调递减,关于点\\((0,0)\\)对称;
借助高中的导数这一工具,我们可以自行做出函数\\(h(x)\\)的图像,如绿色所示。
定义在\\((-\\infty,0)\\cup (0,+\\infty)\\)上,奇函数,在\\((-\\infty,-1)\\)和\\((1,+\\infty)\\)上单调递增,在\\((-1,0)\\)和\\((0,1)\\)上单调递减,关于点\\((0,0)\\)对称;
那么从生物学角度怎么解释呢?
为了好解释,我们不妨对应定义函数\\(f(x)\\)为父本,函数\\(g(x)\\)为母本,函数\\(h(x)\\)为子代;
在某一个性状(比如身高)上,父本和母本中,谁的基因更强大,子代自然就接受谁的遗传基因,也是符合优胜劣汰的自然法则。
定义域的遗传:定义域和母本保持一致,为\\((-\\infty,0)\\cup (0,+\\infty)\\)上
值域的遗传:值域为\\((-\\infty,-2]\\cup [2,+\\infty)\\),二者兼有,并且有变异。
单调性的遗传:由于父本和母本在点\\((1,1)\\)和\\((-1,-1)\\)处相交,故在直线\\(x=-1\\)和直线\\(x=1\\)的两侧单调性可能发生变化。
在区间\\((-\\infty,-1]\\)上,接受父本,单调递增;在\\([-1,0)\\)上,接受母本,单调递减;
在\\((0,1]\\)上,接受母本,单调递减;在\\([1,+\\infty)\\)上接受父本,单调递增。
奇偶性的遗传:同时接受父本和母本,奇函数。
对称性的遗传:同时接受父本和母本,关于点\\((0,0)\\)对称。
那么如何用函数\\(y=x+\\cfrac{1}{x}\\),来研究\\(y=e^x+\\cfrac{1}{e^x}\\)的图像?
那么如何用函数\\(y=e^x\\)和函数\\(y=x^2+2ax(a>0)\\)的性质,来研究\\(y=(x^2+2ax)e^x\\)的图像?