变异简介
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了变异简介相关的知识,希望对你有一定的参考价值。
参考技术A目录
- 1 拼音 2 英文参考 3 注解
1 拼音
biàn yì
2 英文参考
variation
3 注解
变异,遗传的对应词。一般指后代出现与亲代相异的性状的现象,即亲代与子代、子代个体间性状的相异。例如,“一母生九子,连母十个样”生物一方面通过遗传保持自己种类的相对稳定,构成物种存在和发展的基础;另一方面又通过变异以适应变化著的自然环境和生存条件,造成生物不断进化的契机。变异可区分为遗传变异和非遗传变异。日常看到的变异可属两者之一,或为两者的总和。遗传变异可起因于遗传物质的改变,包括基因突变和染色体畸变,也可起因于基因的分离与重组。在生物进化上,只有遗传变异才是自然选择的材料。
变异是同一物种不同世代个体之间,或同代不同个体之间的性状差异。也适用于个体的器官、细胞等次级结构单位。现在把决定生物性状表现的内部主要因素为基因,因为基因通常能够正确地进行自我复制而遗传下去,所以由于基因型不同所引起的变异才是真正的遗传变异。一方面从基因的作用到表现型的过程可受外界环境条件的强烈影响,由环境影响产生的变异是非遗传的变异,其中包括暂时性变异和季节变异等。此外变异还可分为连续变异和不连续变异。由于变异本身和进化问题有很密切的关系,所以自达尔文以来曾受到许多学者的注意。但对由遗传所形成的变异实质,还是在遗传学发展以后才被阐明。此外变异在进化中的作用也是通过群体遗传学的研究而逐渐被阐明的。
变异和遗传是生物的基本特征之一,早就受到学者们的重视。C.达尔文将变异分为:一定变异,如水肥充足一般可使作物的籽粒长得饱满,生活在寒冷地区的兽类一般皮增厚、毛加密等;不定变异,如同一胎牲畜产出的个体之间有差异,同一果实的种子所长出的植株也有差异等;相关变异,如长腿的动物头也长,缺毛的狗,牙齿发育不全等;延续变异,如有的花在人工选择的情况下能连续向着重瓣的方向发生变异等。他还指出,变异有能遗传的与不能遗传的之分,认为只有能遗传的变异才能成为进化和育种的材料。由于时代和科学水平的限制,他还不清楚上述种种变异的性质和原因。现代遗传学告诉我们,引起生物变异主要有三种原因:一是环境条件的改变,一般只能引起表型的变异,这类变异是不遗传的;二是在强烈理化因素影响下基因突变和染色体畸变;三是在有性生殖过程中由于同源染色体的随机分配和非同源染色单体之间的交换而造成的基因重组合。后两类变异是能遗传的变异,只有它们才是生物进化和培育新品种的基础。
遗传变异(基因型)有二种来源:突变是变异的主要来源;基因流(gene flue)和重组也是变异的直接来源。Stebbins(1971)认为突变包括基因突变或点突变和染色体突变。基因流表示居群间的基因交换(杂交产生),而重组带来暸新的基因和等位基因,形成新的基因型,由不同个体带来,增加暸居群的基因型。
单目标优化求解基于matlab集成随机惯性权重和差分变异操作的樽海鞘群算法(ISSA)求解单目标问题含Matlab源码 1858期
一、集成随机惯性权重和差分变异操作的樽海鞘群算法简介
为了提高樽海鞘群算法(Salp Swarm Algorithm,SSA)的收敛速度、计算精度和全局优化能力,在分析总结粒子群优化(Particle Swarm Optimization,PSO)和差分进化(Differential Evolution,DE)算法相关研究成果后,提出了一种集成PSO算法随机惯性权重和DE算法差分变异操作的改进SSA算法——iSSA。首先,将PSO算法的随机惯性权重引入SSA算法的追随者位置更新公式中,用于增强和平衡SSA算法的勘探与开发能力;其次,用DE算法的变异操作替代SSA算法的领导者位置更新操作,以提高SSA算法的收敛速度和计算精度。为了检验随机惯性权重和差分变异操作对SSA算法的改进效果,在多个高维基准函数上进行了仿真实验,并与其他改进SSA算法进行了比较。实验结果及分析表明,与SSA算法和两个典型的改进SSA算法(ESSA和CASSA)相比,集成随机惯性权重和差分变异操作的iSSA算法,在没有增加算法时间复杂度的情况下,显著地提高了SSA算法的收敛速度、计算精度和全局优化能力,并且优于ESSA算法和CASSA算法。
1 本文改进SSA算法的基本策略
SSA算法的核心是领导者和追随者的位置更新操作。PSO算法和DE算法是目前群体智能算法的优秀代表,其丰富的研究成果为SSA算法的改进研究提供了大量有益的参考和启发。本文将PSO算法的随机惯性权重和DE算法的变异操作分别引入SSA算法的式(3)和式(1)中,用于弥补SSA算法的缺点。
1.1 PSO算法随机惯性权重的引入
由SSA算法中的式(3)可知,追随者i的第j维位置xij的更新操作直接受前一个追随者i-1的第j维位置xi−1j的影响。然而,在大多数情况下,追随者i-1的位置对应的解通常较差,从而导致SSA算法易陷入局部最优,收敛速度慢且计算精度低。
在PSO算法中,粒子速度更新直接决定着粒子位置更新。惯性权重是PSO算法粒子速度更新公式中的重要参数,它体现了上一代粒子对当前粒子速度更新的影响力,用于平衡PSO算法的勘探与开发。尽管迄今为止已有大量学者提出了各种PSO算法惯性权重控制策略,但研究表明,在总计18种PSO算法惯性权重控制策略中,除了随机惯性权重以外,常数项惯性权重优于其他所有的惯性权重控制策略。
常数项惯性权重需要繁琐的算法参数调校,因此本文将PSO算法的随机惯性权重引入SSA算法追随者位置更新操作中,从而得到追随者位置更新公式:
xij=12(xij+w×xi−1j) (4)
其中,w为随机惯性权重系数,其取值方法如式(5)[16]所示:
w=0.5+Random (0,1)/2 (5)
其中,Random (0,1)表示均匀分布于(0,1)内的随机数,故w的取值范围为(0.5,1)。显然,此处引入的随机惯性权重没有改变SSA算法的时间复杂度。
1.2 集成DE算法的变异操作
根据SSA算法的式(1),在领导者位置更新操作中,参与者是食物源且没有追随者,缺乏樽海鞘之间的协作和信息共享,容易导致SSA算法过早收敛于较差的局部最优解。
变异操作是DE算法的重要组成部分,它一般通过3个不同的个体来为种群内每一个个体生成一个新个体,通过比例因子可以调节算法开发和勘探之间的平衡。目前DE算法研究中最典型的变异操作有5种,其中与SSA算法的式(1)一样包含最优解且形式最简单的变异操作一般简称为“DE/best/1”。
综上所述,本文提出用DE算法的上述变异操作来替代SSA算法领导者的位置更新操作,从而得到如式(6)所示的领导者位置更新操作:
xij=Fk+r×(xmj-xnj) (6)
针对式(1)和式(6),需要说明以下5点:
(1)根据SSA算法官方网站[18]提供的Matlab版源程序可知,式(1)中的x1j等同于式(6)中的xij,式(1)中的食物源Fj实际上是领导者x1j;只要樽海鞘i的适应度高于领导者的适应度,领导者就被樽海鞘i替代,食物源或最优解也随之被领导者或樽海鞘i替代。
(2)在式(6)中,随机数m和n是互异的樽海鞘编号,说明新生成的樽海鞘i是由最优解、樽海鞘m和樽海鞘n经过差分变异操作合成的。
(3)在式(6)中,互异的下标k和j意味着最优解的异维(跨维)分量参与差分变异操作,有益于增强搜索的广度(开发)和新个体的多样性,避免算法过早陷入局部最优。本文算法程序调试证实了此类异维差分变异操作带来的好处。
(4)式(6)中,系数r的作用类似于DE算法变异操作中的比例因子,经反复测试发现,其是取值范围在(0,1/3)的随机数时效果较好。
(5)与式(1)相比,本文提出的式(6)依然是一种一阶线性关系,没有增加SSA算法的时间复杂度。
二、部分源代码
clearvars
close all
clc
## 三、运行结果
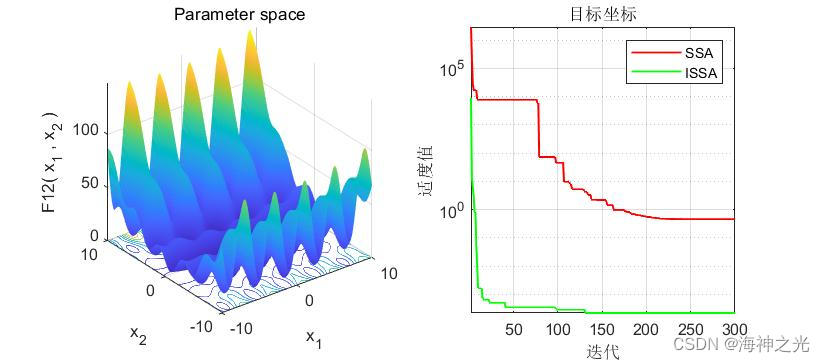
## 四、matlab版本及参考文献
**1 matlab版本**
2014a
**2 参考文献**
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]张志强,鲁晓锋,隋连升,李军怀.集成随机惯性权重和差分变异操作的樽海鞘群算法[J].计算机科学. 2020,47(08)
**3 备注**
简介此部分摘自互联网,仅供参考,若侵权,联系删除
 创作打卡挑战赛
创作打卡挑战赛
 赢取流量/现金/CSDN周边激励大奖
赢取流量/现金/CSDN周边激励大奖
以上是关于变异简介的主要内容,如果未能解决你的问题,请参考以下文章