优先队列优化的 Huffman树 建立
Posted TQCAI
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了优先队列优化的 Huffman树 建立相关的知识,希望对你有一定的参考价值。
如果用vector实现,在运行时遍历寻找最小的两个节点,时间复杂度为O(N^2)
但是我们可以用priority_queue优化,达到O(N logN)的时间复杂度
需要注意的是priority_queue的模板type不能存指针。因为指针是64位整数,存的是数据在内存中的地址。但如果直接存Node
(Node={data;*lChild;*rChild;})的话,因为每次堆调整内存地址都会发生改变,并且因为变量的生命周期,这也无法实现。
所以最好还是用一个Node数组静态实现,左右子树地址保存数组中的索引,这和数据结构中的“静态链表”很相似,这种处理方法在编程中经常用到。
代码:
#include<cstdio> #include<queue> #include<algorithm> using namespace std; int arr[100]; typedef struct Node{ int d,l,r,p; Node(int d=0):d(d){ l=-1; r=-1; } bool operator < (const Node& obj) const { return d>obj.d; } }Node; Node nodes[100]; priority_queue<Node> pq; int main(){ freopen("huffman.txt","r",stdin); int i,n=0; while(~scanf("%d",&i)){ nodes[n]=Node(i); nodes[n].p=n; pq.push(nodes[n]); n++; } while(pq.size()>1){ if(pq.empty()) break; Node a=pq.top(); pq.pop(); if(pq.empty()) break; Node b=pq.top(); pq.pop(); Node c(a.d+b.d); c.l=a.p; c.r=b.p; nodes[n]=c; c.p=n++; pq.push(c); } queue<int> q; q.push(pq.top().p); while(!q.empty()){ int sz=q.size(); while(sz--) { int t=q.front(); q.pop(); printf("%d ",nodes[t].d); if(nodes[t].l>=0) q.push(nodes[t].l); if(nodes[t].r>=0) q.push(nodes[t].r); } puts("") ; } }
测试数据(huffman.txt):
1 5 6 8 6 5 8 7 9 7 3
效果:
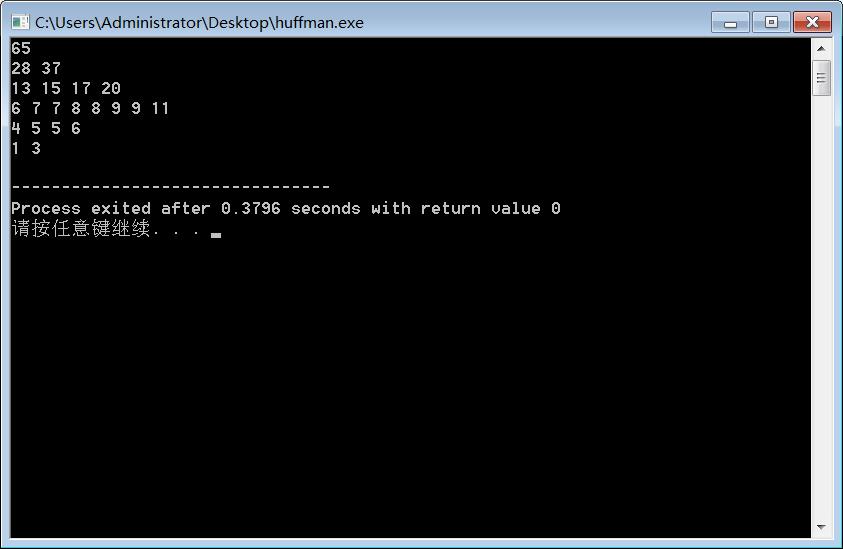
以上是关于优先队列优化的 Huffman树 建立的主要内容,如果未能解决你的问题,请参考以下文章
uva 10954Add All(算法效率+Huffman编码+优先队列)