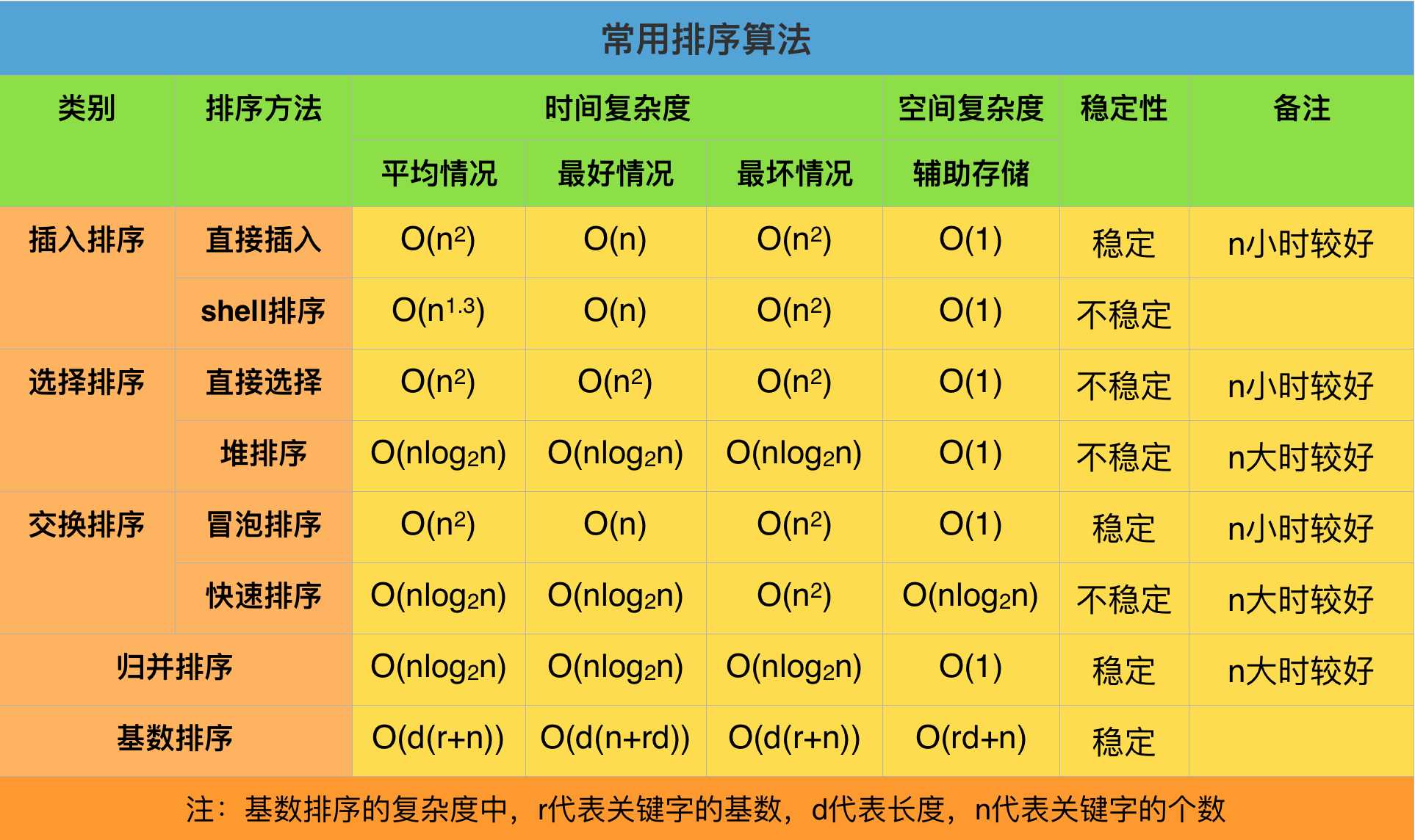
想起排序,感觉就十分的简单了,但是因为以前没有系统学习的原因,这里我还是要记录各种排序,也方便以后回顾

下面的排序算法最优是O(n*log(n)),已经有证明该复杂度是任何用比较元素排序的最优解了
桶排序不是通过比较来排序,所以不受这个下限的影响
插入排序
插入排序由N-1趟完成,对于p = 1到N-1趟,插入排序保证从位置0到位置p上的元素已经为有序的。
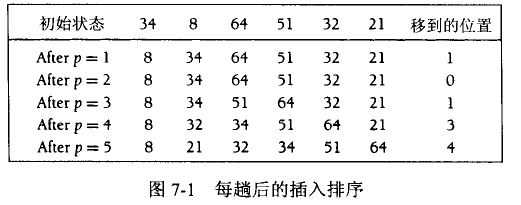
这个过程类似于打扑克的时候,每次拿到一张牌,我们把它在手牌中排好序。
这样的复杂度很明显,O(N*N)

谢尔排序
先选择一个增量序列,比较常用的是用 N/2 作为初始值,然后一直除以2到1,也就是 N/2 N/4 N/8 ... 1 作为增量序列,当然还有其他的;
然后根据上面的序列,把数组分成不同的组,分别对不同的组进行排序,最后当分为一组时,完成最后的排序。
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
最后以1步长进行排序(此时就是简单的插入排序了)。
至于步长的选择,可以看看这里:https://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F
堆排序
每次删除堆的根节点,然后对剩下的堆进行调整,使其继续满足最小(大)堆的性质,这样最后会空出一个空穴,把删除的节点填进去(不必开启额外的空间来存储)
也就是重复 N-1 次下面的操作
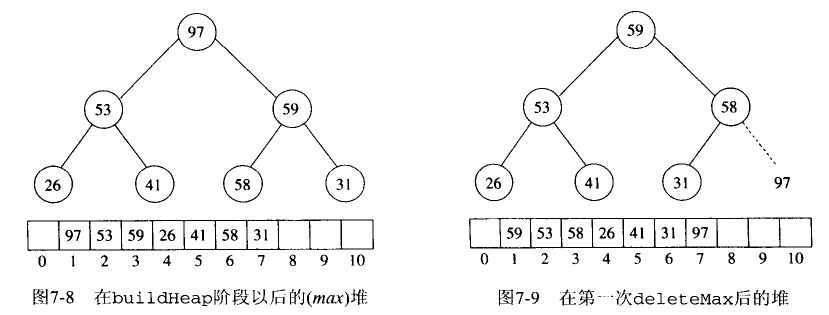
由于需要重新调整堆,而每次恢复堆的复杂度为O(log(N)),所以复杂度为O(N*log(N))
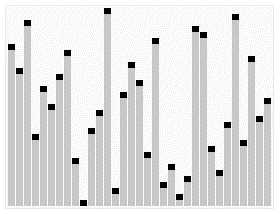
归并排序
不断把数组进行两两合并,每一次合并进行一次排序,最后当两个子数组合并为一个数组后,排序完成
可以看看wiki上的动图,一图在手,算法我有 ヾ(??▽?)ノ

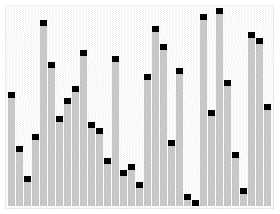
快速排序
这个是排序的老大哥了,简单说来,就是下面几步

这里的枢纽元一般是直接选择第一个,但是书中说这样做不好,为什么呢?因为如果输入的不是乱序,是有序的数组,就不得不做没用的划分,有兴趣可以自己探讨
另外,书中也说起当N小于20,快速排序并不比插入排序好
间接排序
先想一下这个的意义,因为有些语言交换大数据元素的效率比较慢,如果可以定义表示数组位置的指针之类的,那么原数组可以不用改变位置,我们可以用这个新数组来表示排序后的顺序
例如:数组 4 3 1 2 5
建立索引数组 0 1 2 3 4
排序后索引 2 3 1 0 4
桶排序
要求输入的数据 A1, A2...AN,必须是由小于M的正整数组成,步骤很简单:
1.使用一个大小为M的count数组
2.遍历数据,每读一个Ai,count[Ai] + 1
扫描整个数组后,就可以打印出排序后的表,平均复杂度为O(N)
外部排序
和上面归并排序很像,只不过每次的归并是从文件中读数据再写入文件,为什么这样做?因为当数据很大的时候,需要把数据分批排序写进多个文件。
 假设有4个文件,一个文件有一组数据,如何用这个算法来排序?
假设有4个文件,一个文件有一组数据,如何用这个算法来排序?

现在内存一次只能读M=3个数据,那么分开排序

然后归并

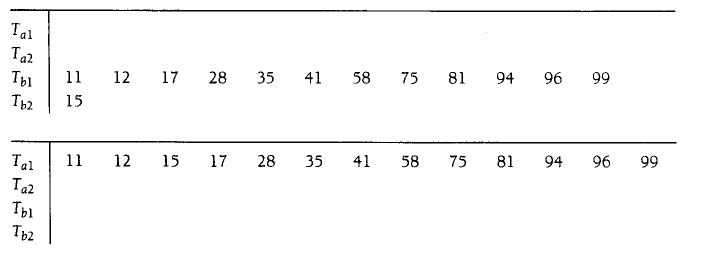
总结