树链剖分整理
Posted _kangkang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树链剖分整理相关的知识,希望对你有一定的参考价值。
树链剖分整理总结
问题的设置:
对于一棵树(无向无环连通图),为每个结点分配对应的权重。要求能高效计算任意两个结点之间的路径的各类信息,其中包括路径长度(路径上所有结点的权重加总),路径中最大权重,最小权重等等。到这里一切都还是比较简单的,我们可以利用 Tarjan 的 LCA 算法在线性时间复杂度内快速求解。但是如果还要求允许动态修改任意结点的权值,那么问题就不简单了。很容易发现这有些类似于线段树的问题,但是线段树是作用在区间上,而我们的问题是发生在树上的,因此线段树并不适用。而树链剖分则是可以用于求解这类问题的高效算法,其更新权值的时间复杂度为 $O(logn)$ 而统计路径信息的时间复杂度为 $O(log^2n)$。
树链剖分通常用于处理树的形态不变 但点权/边权需要修改查询的题目。
理解:
树链剖分就是将树分割成多条互不相交的轻重链,然后利用数据结构(线段树、树状数组等)来维护这些链。
首先就是一些必须知道的概念:
- 重节点:子树结点数目最多的节点;
- 轻节点:除了重结点以外的节点;
- 重边:父亲节点和重节点连成的边;
- 轻边:父亲节点和轻节点连成的边;
- 重链:由多条重边连接而成的路径;
- 轻链:由多条轻边连接而成的路径;
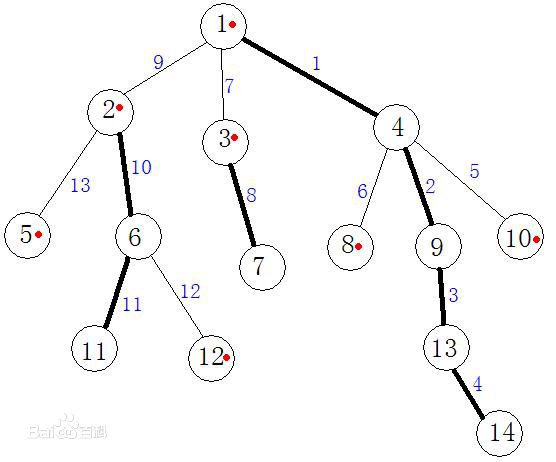
比如上面这幅图中,粗黑色的边就是重边,连续的重边连起来就是重链,1,2,3,5,12,8,10 为轻节点,其余为重节点,用红点标记的就是该结点所在链的起点,还有每条边的值其实是进行 dfs 时的执行序号。理解树链剖分算法其实不用管轻节点和轻链,把底端的轻节点看成由本身一个节点形成的重链,这样所有节点都在重链上。
具体实现:
1. 一条重链在线段树上是一段连续的区间。
2. 一个节点的重儿子就是这个节点的子节点中子树最大的点。
3. 记录链需要记录链最顶上的点,记作 top。具体实现,是基于两次 dfs。第一次 dfs 求出重儿子。第二次 dfs,通过节点映射时间戳,优先 dfs 重儿子,得出节点新编号,就可以得到上述需要满足的点。
时间复杂度:
性质1:如果 $(u, v)$ 是一条轻边,那么 $size(v) < size(u)/2$;
证明:由于任一轻儿子对应的子树大小要小于父节点所对应子树大小的一半,因此从一个轻儿子沿轻边向上走到父节点后 所对应的子树大小至少变为两倍以上;
性质2:从任一节点向根节点走,走过的重链和轻边的条数都是 $logn$ 级别以内的;
证明:基于性质1,显然经过的轻边条数是不超过 $logn$ 的,然后由于重链都是间断的 (连续的可以合成一条),所以经过的重链的条数是不超过轻边条数 $+1$ 的,因此经过重链的条数也是 $logn$ 级别的;
通过链的划分,就可以满足在求 lca 的时候,因为基于线段树,处理节点到所在重链顶端的数据的复杂度就是 $O(logn)$,又由性质2,则统计或修改路径信息的时间复杂度为 $O(log^2n)$,修改单点权值时间复杂度为 $O(logn)$;
树链的建立只涉及到了深度优先搜索,时间复杂度为 $O(n)$,而线段树在知道初始值时可以以 $O(n)$ 时间复杂度建立,因此预处理的时间复杂度为 $O(n)$。
所以总的时间复杂度为 $O(n + Qlog^2n)$。( $Q$ 为询问和操作次数)。
实战
1. 洛谷P3384【模板】树链剖分 (基于点权,路径、子树更新、查询)
树链剖分+线段树模板代码:

1 #include <stdio.h> 2 #include <iostream> 3 #define REP(i, a, b) for (int i = a; i <= b; i++) 4 using namespace std; 5 typedef long long LL; 6 const int MAXN = 110000; 7 struct Node { 8 int to, next; 9 } edg[MAXN<<1]; 10 struct segmentTree { 11 int left, right; 12 LL sum, tag; 13 } tree[MAXN<<2]; 14 int head[MAXN], siz[MAXN], top[MAXN], hson[MAXN], dep[MAXN], fa[MAXN], id[MAXN], rnk[MAXN]; 15 /* 16 head[u]:前向星储存边中保存节点u最后添加的边的编号 17 siz[u]:保存以u为根的子树的节点个数 18 top[u]:保存当前节点所在链的顶端节点 19 hson[u]:保存节点u的重儿子 20 dep[u]:保存节点u的深度值 21 fa[u]:保存节点u的父亲节点编号 22 id[u]:保存节点u剖分以后的新编号(dfs2执行顺序) 23 rnk[u]:u为新编号,rnk[u]为原编号 24 */ 25 int N, M, R, A[MAXN], idx = 0, dfs_cnt = 0; 26 LL mod; 27 inline int read() { // 读入优化 28 int x = 0, f = 1; char ch = getchar(); 29 while (ch < \'0\' || ch > \'9\') { if (ch == \'-\') f = -1; ch = getchar(); } 30 while (ch >= \'0\' && ch <= \'9\') { x = x * 10 + ch - \'0\'; ch = getchar(); } 31 return x * f; 32 } 33 inline void adde(int u, int v) { // 链式前向星添加u向v的边 34 edg[++idx].to = v; edg[idx].next = head[u]; head[u] = idx; 35 } 36 /* 第一次DFS可以得到当前节点的父亲结点(fa数组)、 37 当前结点的深度值(dep数组)、当前结点的子结点数量(siz数组)、 38 当前结点的重结点(hson数组) */ 39 void dfs1(int u, int father, int depth) { 40 dep[u] = depth; 41 fa[u] = father; 42 siz[u] = 1; 43 for (int i = head[u]; i; i = edg[i].next) { 44 int v = edg[i].to; 45 if (v != fa[u]) { 46 dfs1(v, u, depth + 1); 47 siz[u] += siz[v]; 48 if (hson[u] == -1 || siz[v] > siz[hson[u]]) hson[u] = v; 49 } 50 } 51 } 52 /* 第二次DFS的时候则可以将各个重节点连接成重链,轻节点连接成轻链, 53 并且将重链(其实就是一段区间)用数据结构(一般是树状数组或线段树) 54 来进行维护,为每个节点进行编号,其实就是DFS在执行时的顺序(id数组), 55 以及当前节点所在链的起点(top数组),还有当前节点在树中的位置(rnk数组)。 */ 56 void dfs2(int u, int t) { 57 id[u] = ++dfs_cnt; rnk[dfs_cnt] = u; top[u] = t; 58 if (!hson[u]) return ; 59 dfs2(hson[u], t); 60 for (int i = head[u]; i; i = edg[i].next) { 61 int v = edg[i].to; 62 if (v != hson[u] && v != fa[u]) dfs2(v, v); 63 } 64 } 65 void buildtree(int i, int l, int r) { // 建线段树 66 tree[i].left = l; tree[i].right = r; 67 // 注意线段树维护的节点的编号是dfs2后的新编号,不是原节点编号 68 // 因此此处通过rnk[l]得出原节点编号 69 if (l == r) tree[i].sum = A[rnk[l]]; 70 else { 71 int mid = (l + r) >> 1; 72 buildtree(i << 1, l , mid); 73 buildtree(i << 1 | 1, mid + 1, r); 74 tree[i].sum = tree[i<<1].sum + tree[i<<1|1].sum; 75 } 76 } 77 void pushdown(int i) { // 线段树上i节点向下更新一层 78 int l = i << 1, r = i << 1 | 1; 79 tree[l].sum += (tree[l].right - tree[l].left + 1) * tree[i].tag; 80 tree[r].sum += (tree[r].right - tree[r].left + 1) * tree[i].tag; 81 tree[l].tag += tree[i].tag; 82 tree[r].tag += tree[i].tag; 83 tree[i].tag = 0; 84 } 85 void update(int i, int x, int y, LL z) { // 当前线段树上节点为i,在区间[x, y]上成段增加z 86 int l = i << 1, r = i << 1 | 1; 87 if (tree[i].left > y || tree[i].right < x) return ; 88 if (x <= tree[i].left && tree[i].right <= y) { 89 tree[i].sum += (tree[i].right - tree[i].left + 1) * z; 90 tree[i].tag += z; 91 } else { 92 if (tree[i].tag) pushdown(i); 93 update(l, x, y, z); 94 update(r, x, y, z); 95 tree[i].sum = tree[l].sum + tree[r].sum; 96 } 97 } 98 LL query(int i, int x, int y) { // 当前线段树上节点为i,查询区间[x, y]的和 99 int l = i << 1, r = i << 1 | 1; 100 if (x <= tree[i].left && tree[i].right <= y) return tree[i].sum; 101 if (tree[i].left > y || tree[i].right < x) return 0; 102 if (tree[i].tag) pushdown(i); 103 return query(l, x, y) + query(r, x, y); 104 } 105 void update_path(int u, int v, LL z) { // 从u到v节点最短路径上所有节点的值都加上z 106 int tu = top[u], tv = top[v]; 107 while (tu != tv) { 108 if (dep[tu] < dep[tv]) swap(u, v), swap(tu, tv); 109 update(1, id[tu], id[u], z); 110 u = fa[tu], tu = top[u]; 111 } 112 if (dep[u] < dep[v]) swap(u, v); 113 update(1, id[v], id[u], z); 114 } 115 LL query_path(int u, int v) { // 求树从u到v结点最短路径上所有节点的值之和 116 LL res = 0; 117 int tu = top[u], tv = top[v]; 118 // 计算节点到所在重链起始点的路径和直到两个节点在同一条链上 119 // 注意每次循环只能跳一次,并且让结点深的那个来跳到top的位置,避免两个一起跳从而插肩而过。 120 while (tu != tv) { 121 if (dep[tu] < dep[tv]) swap(u, v), swap(tu, tv); 122 res += query(1, id[tu], id[u]); 123 u = fa[tu], tu = top[u]; 124 } 125 // 即使两个节点在同一条链上,仍需要再计算一次路径和,因为最后一次更新u,v后是没有计算的 126 if (dep[u] < dep[v]) swap(u, v); 127 return res + query(1, id[v], id[u]); 128 } 129 130 int main() { 131 N = read(), M = read(), R = read(), mod = read(); 132 REP(i, 1, N) A[i] = read(); 133 REP(i, 2, N) { 134 int u = read(), v = read(); 135 adde(u, v); adde(v, u); 136 } 137 dfs1(R, 0, 1); 138 dfs2(R, R); 139 buildtree(1, 1, N); 140 while (M--) { 141 int opt = read(); 142 switch (opt) { 143 case 1: { 144 int x = read(), y = read(); 145 LL z; scanf("%lld", &z); 146 update_path(x, y, z); 147 break; 148 } 149 case 2: { 150 int x = read(), y = read(); 151 printf("%lld\\n", query_path(x, y) % mod); 152 break; 153 } 154 case 3: { 155 int x = read(); 156 LL z; scanf("%lld", &z); 157 update(1, id[x], id[x] + siz[x] - 1, z); 158 break; 159 } 160 case 4: { 161 int x = read(); 162 printf("%lld\\n", query(1, id[x], id[x] + siz[x] - 1) % mod); 163 } 164 } 165 } 166 return 0; 167 }
2. POJ 2763 -- Housewife Wind (基于边权,单点更新,区间查询)
基于边权的树链剖分,对于边来说,除了根节点外,其他所有的边都可以与其子节点一一对应,这样就转换为了点权问题,在处理时要注意LCA当前点不统计,因为此时的边权不会被访问到。
树链剖分+树状数组代码:

1 #include <iostream> 2 #include <stdio.h> 3 #include <cstring> 4 #define MAXN 100010 5 using namespace std; 6 typedef long long LL; 7 struct edg{ 8 int to, next, val; 9 } edg[MAXN<<1]; 10 int idx, tol, head[MAXN], cost[MAXN], c[MAXN], xx[MAXN], yy[MAXN]; 11 // cost映射树上原编号的节点值,c为树状数组 12 int hson[MAXN], fa[MAXN], id[MAXN], dep[MAXN], siz[MAXN], top[MAXN]; 13 int n, q, s; 14 // 前向星添加u向v的边 15 void add_edg(int u, int v, int z) { 16 edg[++idx].to = v; 17 edg[idx].val = z; 18 edg[idx].next = head[u]; 19 head[u] = idx; 20 } 21 // 取x的二进制中1的最低位代表的值 22 int lowbit(int x) { 23 return x & -x; 24 } 25 // 树状数组中向原树上编号为x(新编号)的节点加上值val 26 void update(int x, int val) { 27 for (; x <= n; x += lowbit(x)) c[x] += val; 28 } 29 // 树状数组查询原树上[1, x]的节点值之和 30 LL query(int x) { 31 if (!x) return 0; 32 LL sum = 0; 33 for (; x > 0; x -= lowbit(x)) sum += c[x]; 34 return sum; 35 } 36 // 查询u、v之间最短路径边权和(u, v为树上原编号) 37 LL query_path(int u, int v) { 38 LL ans = 0; 39 int tu = top[u], tv = top[v]; 40 while (tu != tv) { 41 if (dep[tu] < dep[tv]) swap(tu, tv), swap(u, v); 42 ans += query(id[u]) - query(id[tu] - 1); 43 u = fa[tu]; 44 tu = top[u]; 45 } 46 if (dep[u] < dep[v]) swap(u, v); 47 ans += query(id[u]) - query(id[v]); 48 return ans; 49 } 50 void dfs1(int u, int father, int depth) { 51 dep[u] = depth; 52 fa[u] = father; 53 siz[u]++; 54 for (int i = head[u]; ~i; i = edg[i].next) { 55 int v = edg[i].to; 56 if (v != fa[u]) { 57 cost[v] = edg[i].val; 58 dfs1(v, u, depth + 1); 59 siz[u] += siz[v]; 60 if (hson[u] == -1 || siz[hson[u]] < siz[v]) hson[u] = v; 61 } 62 } 63 } 64 void dfs2(int u, int t) { 65 id[u] = ++tol; 66 update(id[u], cost[u]); 67 top[u] = t; 68 if (hson[u] == -1) return ; 69 dfs2(hson[u], t); 70 for (int i = head[u]; ~i; i = edg[i].next) { 71 int v = edg[i].to; 72 if (v != fa[u] && v != hson[u]) dfs2(v, v); 73 } 74 } 75 void init() { 76 cost[1] = cost[0] = idx = tol = 0; 77 memset(siz, 0, sizeof(siz)); 78 memset(top, -1, sizeof(top)); 79 memset(hson, -1, sizeof(hson)); 80 memset(c, 0, sizeof(c)); 81 memset(head, -1, sizeof(head)); 82 } 83 84 int main() { 85 while (~scanf("%d %d %d", &n, &q, &s)) { 86 init(); 87 for (int i = 1; i < n; i++) { 88 int z; 89 scanf("%d %d %d", &xx[i], &yy[i], &z); 90 add_edg(xx[i], yy[i], z); 91 add_edg(yy[i], xx[i], z); 92 } 93 dfs1(1, -1, 1); 94 dfs2(1, 1); 95 while (q--) { 96 int op; 97 scanf("%d", &op); 98 if (op == 0) { 99 int to; 100 scanf("%d", &to); 101 printf("%lld\\n", query_path(s, to)); 102 s = to; 103 } else { 104 int ith, newv; 105 scanf("%d %d", &ith, &newv); 106 if (dep[xx[ith]] < dep[yy[ith]]) swap(xx[ith], yy[ith]); 107 update(id[xx[ith]], newv - (query(id[xx[ith]]) - query(id[xx[ith]] - 1))); 108 } 109 } 110 } 111 return 0; 112 }
3.POJ 3237 -- Tree (基于边权,区间标记)
树链剖分+线段树代码:

1 #include <stdio.h> 2 #include <iostream> 3 #include <string> 4 #include <cstring> 5 #define REP(i, a, b) for (int i = a; i <= b; i++) 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 typedef long long LL; 9 const int MAXN = 10010; 10 struct Node { 11 int to, next, val; 12 } edg[MAXN<<1]; 13 // 线段树维护区间最大最小值,tag为取相反数标记 14 struct segmentTree { 15 int left, right; 16 int maxx, minn; 17 int tag; 18 } tree[MAXN<<2]; 19 int head[MAXN], siz[MAXN], top[MAXN], hson[MAXN], dep[MAXN], fa[MAXN], id[MAXN]; 20 int n, xx[MAXN], yy[MAXN], val1[MAXN], val2[MAXN], idx, dfs_cnt; 21 // val1映射树上原编号的节点值,val2映射dfs2后新编号的节点值 22 LL mod; 23 // 读入优化 24 inline int read() { 25 int x = 0, f = 1; char ch = getchar(); 26 while (ch < \'0\' || ch > \'9\') { if (ch == \'-\') f = -1; ch = getchar(); } 27 while (ch >= \'0\' && ch <= \'9\') { x = x * 10 + ch - \'0\'; ch = getchar(); } 28 return x * f; 29 } 30 void init() { 31 val1[0] = val1[1] = idx = dfs_cnt = 0; 32 memset(head, -1, sizeof(head)); 33 memset(hson, -以上是关于树链剖分整理的主要内容,如果未能解决你的问题,请参考以下文章
