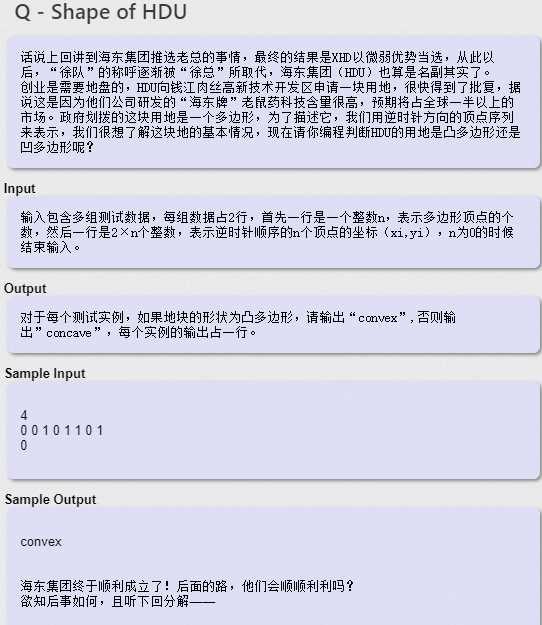
这道题的话,我拿到题是有点懵圈的,如果要我自己判断的话,我也要自己在纸上建立坐标轴然后一一将点标出,后用肉眼判断。这个用代码实现嘛……
后来就只能参考大神们的算法啦。
判断方法:
向量a=(x1,y1),b=(x2,y2);
向量的叉积a×b=x1*y2-x2*y1; 当a×b>0时,b在a的逆时针方向,当a×b=0时,b与a共线,当a×b<0时,b在a的顺时针方向。
对于连续输入的三点A(x1,y1),B(x2,y2),C(x3,y3);
根据凸多边形的性质:向量AC(x3-x1,y3-y1)必定在向量AB(x2-x1,y2-y1)的逆时针方向,或者共线。
所以AB×AC>=0,即ans=(x2-x1)*(y3-y1)-(x3-x1)*(y2-y1)>=0。 当出现ans<0时,即为凹多边形。
该题要判断所有点吗,如果只要有个点不成立,那么该多边形就是凹变形。如果该多边形要是凸变形,那所有的点都要成立。
源地址:http://blog.csdn.net/wangkemingshishuaige/article/details/47658267
太强了。
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cmath> 5 #include <deque> 6 #include <vector> 7 #include <queue> 8 #include <string> 9 #include <cstring> 10 #include <map> 11 #include <stack> 12 #include <set> 13 #include<cstdlib> 14 #include<ctype.h> 15 using namespace std; 16 typedef long long ll; 17 #define pi 3.14159265358979323846264338327 18 #define E 2.71828182846 19 #define INF 0x3f3f3f3f 20 #define maxn 555555 21 struct node 22 { 23 int x, y; 24 }p[11000]; 25 bool judge(int x1, int y1, int x2, int y2, int x3, int y3) 26 { 27 return (x2 - x1)*(y3 - y1) - (x3 - x1)*(y2 - y1) >= 0; 28 } 29 int main() 30 { 31 int n, i, flage; 32 while (scanf("%d", &n) != EOF&&n != 0) 33 { 34 flage = 0; 35 for (i = 0; i<n; i++) 36 scanf("%d%d", &p[i].x, &p[i].y); 37 if (!judge(p[n - 1].x, p[n - 1].y, p[0].x, p[0].y, p[1].x, p[1].y)) 38 flage = 1; 39 if (!judge(p[n - 2].x, p[n - 2].y, p[n - 1].x, p[n - 1].y, p[0].x, p[0].y)) 40 flage = 1; 41 for (i = 0; i<n - 2; i++) 42 { 43 if (flage) 44 break; 45 if (!judge(p[i].x, p[i].y, p[i + 1].x, p[i + 1].y, p[i + 2].x, p[i + 2].y)) 46 flage = 1; 47 } 48 if (flage) 49 printf("concave\\n"); 50 else 51 printf("convex\\n"); 52 } 53 return 0; 54 }