网格顶点坐标的3个分量当做3个独立的标量场，如此，三角面片便有3个独立的梯度场，是为网格内在属性。当顶点移动时，问题便为求解方程
，
根据变分法得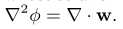
其中Φ是为形变后的顶点坐标，W为形变后的梯度场。方程进一步用矩阵表示为 
，L为网格拉普拉斯矩阵，b为梯度场的散度.
1.定义梯度算子
设 f 为分段线性函数，网格三角面片{Xi, Xj, Xk}的顶点处有：f(Xi) = fi ; f(Xj) = fj ; f(Xk) = fk; u = (a, b)是三角面片的重心坐标，Bi, Bj, Bk是三角面片的一次拉格朗日
插值函数，通过线性插值，f 在三角面片上的梯度表示为
。
函数Bi,Bj,Bk满足Bi(u) + Bj(u) + Bk(u) = 1，所以Bi(u) + Bj(u) + Bk(u)的梯度等于0，所以 f 的梯度可表示为
。
定义函数B的梯度为顶点到对边的高的倒数，方向为对边指向顶点。B的梯度表示为
，A表示三角形面积，⊥表示旋转90度。
2. 定义散度算子
设置向量值函数w：S——R3 。
S表示网格，W表示三角面片上的各个顶点向量，那么W的散度为
。
3. 拉普拉斯算子
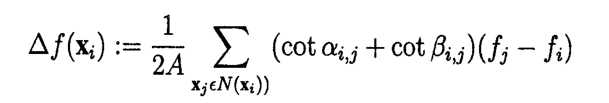
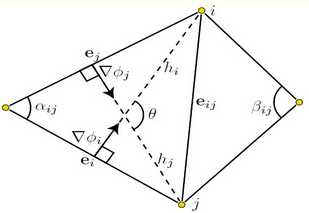
构建拉普拉斯矩阵
1 void mainNode::InitLpls() 2 { 3 int vertexNumber = m_vecAllVertex.size(); 4 //构建拉普拉斯矩阵权值，方式二 5 for (int i = 0; i < vertexNumber; i++) 6 { 7 pVERTEX pVertex = m_vecAllVertex.at(i); 8 float totalWeight = 0.0; 9 for (int j = 0; j < pVertex->vecNeighborEdge.size(); j++) 10 { 11 pEDGE pEdge = pVertex->vecNeighborEdge.at(j); 12 pVERTEX pA = pEdge->pA; 13 pVERTEX pB = pEdge->pB; 14 15 pVERTEX pTarget; 16 if (pA->id == pVertex->id) 17 pTarget = pB; 18 else 19 pTarget = pA; 20 21 std::vector<pTRIANGLE> vecTri = pEdge->vecNeighborTri; 22 pVERTEX pC = NULL; 23 float weight = 0.0; 24 for (int k = 0; k < vecTri.size(); k++) 25 { 26 pTRIANGLE pTri = vecTri.at(k); 27 pVERTEX p1 = pTri->pA; 28 pVERTEX p2 = pTri->pB; 29 pVERTEX p3 = pTri->pC; 30 if ((pA->id == p1->id && pB->id == p2->id) || (pA->id == p2->id && pB->id == p1->id)) 31 { 32 pC = p3; 33 } 34 else if ((pA->id == p1->id && pB->id == p3->id) || (pA->id == p3->id && pB->id == p1->id)) 35 { 36 pC = p2; 37 } 38 else if ((pA->id == p2->id && pB->id == p3->id) || (pA->id == p3->id && pB->id == p2->id)) 39 { 40 pC = p1; 41 } 42 //开始求取权值 43 float cotAngle = 0.0; 44 GetCotAngle(pA->pos, pB->pos, pC->pos, cotAngle); 45 weight += cotAngle; 46 } 47 weight /= 2.0; 48 pVertex->mapWeightForOther.insert(std::pair<int, float>(pTarget->id, weight) ); 49 totalWeight += weight; 50 } 51 pVertex->fTotalWeight = totalWeight; 52 } 53 //计算拉普拉斯坐标。方式二 54 for (int i = 0; i < vertexNumber; i++) 55 { 56 pVERTEX pVertex = m_vecAllVertex.at(i); 57 osg::Vec3 pos = pVertex->pos; 58 pos = pos * pVertex->fTotalWeight; 59 osg::Vec3 otherPos = osg::Vec3(0.0, 0.0, 0.0); 60 for (int j = 0; j < pVertex->vecNeighborVertex.size(); j++) 61 { 62 pVERTEX pNeihbor = pVertex->vecNeighborVertex.at(j); 63 std::map<int, float>::iterator itor = pVertex->mapWeightForOther.find(pNeihbor->id); 64 float weight = itor->second; 65 otherPos += pNeihbor->pos * weight; 66 } 67 pVertex->lplsPos = pos - otherPos; 68 } 69 70 int count = 0; 71 std::vector<int> beginNumber(vertexNumber); 72 for (int i = 0; i < vertexNumber; i++) 73 { 74 beginNumber[i] = count; 75 count += m_vecAllVertex[i]->vecNeighborVertex.size() + 1; 76 } 77 78 std::vector<Eigen::Triplet<float> > vectorTriplet(count); 79 for (int i = 0; i < vertexNumber; i++) 80 { 81 pVERTEX pVertex = m_vecAllVertex.at(i); 82 //原始拉普拉斯矩阵 83 vectorTriplet[beginNumber[i]] = Eigen::Triplet<float>(i, i, pVertex->fTotalWeight); 84 //更改后 85 //vectorTriplet[beginNumber[i]] = Eigen::Triplet<float>(i, i, -pVertex->fTotalWeight); 86 87 int j = 0; 88 std::map<int, float>::iterator itor; 89 for(itor = pVertex->mapWeightForOther.begin(); itor != pVertex->mapWeightForOther.end(); itor++) 90 { 91 int neighborID = itor->first; 92 float weight = itor->second; 93 //原始拉普拉斯矩阵 94 vectorTriplet[beginNumber[i] + j + 1] = Eigen::Triplet<float>(i, neighborID, -weight); 95 //更改后 96 //vectorTriplet[beginNumber[i] + j + 1] = Eigen::Triplet<float>(neighborID, i, weight); 97 j++; 98 } 99 } 100 101 //头一圈和顶一圈 102 for (int i = 0; i < m_iAroundNumber * 2; i++) 103 { 104 float weight = 1.0; 105 pVERTEX pVertex; 106 if (i < m_iAroundNumber) 107 { 108 pVertex = m_vecAllVertex.at(i); 109 } 110 else 111 { 112 pVertex = m_vecAllVertex.at(i + m_iAroundNumber * 14); 113 } 114 115 int row = i + vertexNumber; 116 vectorTriplet.push_back(Eigen::Triplet<float>(row, pVertex->id, weight)); 117 } 118 119 120 121 m_Matrix.resize(vertexNumber + m_iAroundNumber * 2, vertexNumber); 122 //m_Matrix.resize(vertexNumber, vertexNumber); 123 m_Matrix.setFromTriplets(vectorTriplet.begin(), vectorTriplet.end()); 124 //std::cout << m_Matrix << std::endl; 125 }
计算梯度
1 void mainNode::CalculateGradient() 2 { 3 std::map<int, pTRIANGLE>::iterator itorOfTri; 4 for (itorOfTri = m_mapAllTri.begin(); itorOfTri != m_mapAllTri.end(); itorOfTri++) 5 { 6 int triID = itorOfTri->first; 7 pTRIANGLE pTri = itorOfTri->second; 8 osg::Vec3 A = pTri->pA->pos; 9 osg::Vec3 B = pTri->pB->pos; 10 osg::Vec3 C = pTri->pC->pos; 11 12 13 osg::Vec3 AB = B - A; 14 osg::Vec3 CA = A - C; 15 osg::Vec3 BC = C - B; 16 17 osg::Vec3 normal = ((B - A) ^ (C - A)); 18 //三角形面积 19 float area = normal.length() * 0.5; 20 normal.normalize(); 21 22 float times = 2.0; 23 osg::Vec3 vecGradientX = ((normal ^ BC) / (times * area) * A.x()) + ((normal ^ AB) / (times * area) * C.x()) + ((normal ^ CA) / (times * area) * B.x()); 24 osg::Vec3 vecGradientY = ((normal ^ BC) / (times * area) * A.y()) + ((normal ^ AB) / (times * area) * C.y()) + ((normal ^ CA) / (times * area) * B.y()); 25 osg::Vec3 vecGradientZ = ((normal ^ BC) / (times * area) * A.z()) + ((normal ^ AB) / (times * area) * C.z()) + ((normal ^ CA) / (times * area) * B.z()); 26 pTri->vecGradient[0] = vecGradientX; 27 pTri->vecGradient[1] = vecGradientY; 28 pTri->vecGradient[2] = vecGradientZ; 29 } 30 }
计算散度
1 void mainNode::CalculateDivergence() 2 { 3 4 for (int i = 0; i < m_vecAllVertex.size(); i++) 5 { 6 pVERTEX pVertex = m_vecAllVertex.at(i); 7 std::vector<pTRIANGLE> vecTri= pVertex->vecNeighborTri; 8 9 float divergenceX, divergenceY, divergenceZ; 10 divergenceX = divergenceY = divergenceZ = 0.0; 11 12 for (int j = 0; j < vecTri.size(); j++) 13 { 14 pTRIANGLE pTri = vecTri.at(j); 15 pVERTEX pA = pTri->pA; 16 pVERTEX pB = pTri->pB; 17 pVERTEX pC = pTri->pC; 18 //A为主顶点 19 osg::Vec3 A, B, C; 20 if (pA->id == pVertex->id) 21 { 22 A = pA->pos; 23 B = pB->pos; 24 C = pC->pos; 25 } 26 else if (pB->id == pVertex->id) 27 { 28 A = pB->pos; 29 B = pC->pos; 30 C = pA->pos; 31 } 32 else if (pC->id == pVertex->id) 33 { 34 A = pC->pos; 35 B = pA->pos; 36 C = pB->pos; 37 } 38 // 39 osg::Vec3 AB, AC; 40 float cotAngleABC, cotAngleACB; 41 AB = B - A; 42 AC = C - A; 43 GetCotAngle(A, C, B, cotAngleABC); 44 GetCotAngle(A, B, C, cotAngleACB); 45 46 for (int k = 0; k < 3; k++) 47 { 48 float divergenceTemp = 0 - 0.5 * (cotAngleABC * (AC * pTri->vecGradient.at(k)) + cotAngleACB * (AB * pTri->vecGradient.at(k))); 49 if (k == 0) 50 { 51 divergenceX += divergenceTemp; 52 } 53 else if (k == 1) 54 { 55 divergenceY += divergenceTemp; 56 } 57 else if(k == 2) 58 { 59 divergenceZ += divergenceTemp; 60 } 61 } 62 } 63 64 pVertex->vecDivergence[0] = divergenceX; 65 pVertex->vecDivergence[1] = divergenceY; 66 pVertex->vecDivergence[2] = divergenceZ; 67 } 68 69 }
参考论文：
Mesh Editing with Poisson-Based Gradient Field Manipulation
三角网格曲面上的Laplace算子及其应用
http://blog.sina.com.cn/s/blog_73428e9a0101h4l9.html