机器学习梯度下降与正规方程(附例题代码)
Posted 大拨鼠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习梯度下降与正规方程(附例题代码)相关的知识,希望对你有一定的参考价值。
文章目录
梯度下降
对于代价函数 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1),或者我们可以推广到更一般的代价函数(系数更多),如 J ( θ 0 , θ 1 , θ 2 , . . . , θ n ) J(θ_0,θ_1,θ_2,...,θ_n) J(θ0,θ1,θ2,...,θn),如果要最小化代价函数 m i n min min J ( θ 0 , θ 1 , θ 2 , . . . , θ n ) J(θ_0,θ_1,θ_2,...,θ_n) J(θ0,θ1,θ2,...,θn),那么我们可以用梯度下降法来解决,下面会以两个参数的代价函数为例对梯度下降法进行介绍:
- 给 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)的两个参数 θ 0 θ_0 θ0和 θ 1 θ_1 θ1赋两个初始值,这个值可以随意,但通常会选择将 θ 0 θ_0 θ0和 θ 1 θ_1 θ1均设为0。
- 不停地一点点改变 θ 0 θ_0 θ0和 θ 1 θ_1 θ1,使代价函数 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)越来越小,直到找到最小值。
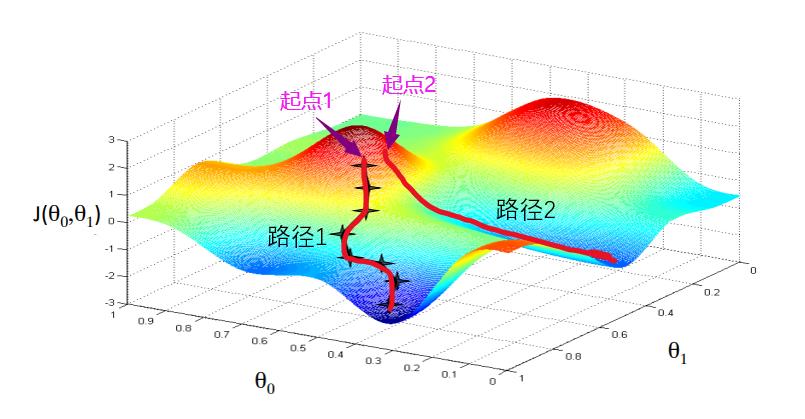
以下图为例,我们初始设定的 θ 0 θ_0 θ0和 θ 1 θ_1 θ1对应图中的某个点,我们将这个点记为起点1,现在从起点1出发,沿路径1收敛于局部的最低点,也就是局部最优解。如果我们的起点往右偏移一点得到起点2,那么第二个局部最优解应该是沿路径2收敛的最小值。同理,如果起点1往右偏移一点,也会得到不同的最优解。
下面我们来看看梯度下降算法的数学原理:
重复下面这行算法,不断更新参数 θ j θ_j θj,直到收敛于最小值,其中 : = := :=表示赋值, α α α表示学习率(learning rate),这里表示梯度下降的快慢, ∂ ∂ θ j J ( θ 0 , θ 1 ) \\frac∂∂θ_jJ(θ_0,θ_1) ∂θj∂J(θ0,θ1)是导数项,先不用管,之后会进行详细解释
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( f o r j = 0 a n d j = 1 ) θ_j:=θ_j-α\\frac∂∂θ_jJ(θ_0,θ_1) \\quad(for \\ j=0\\ and\\ j=1) θj:=θj−α∂θj∂J(θ0,θ1)(for j=0 and j=1)
上面我们说到了要不断改变 θ 0 θ_0 θ0和 θ 1 θ_1 θ1的值,那么如何改变呢,也是利用上面这一行算法,并且改变 θ 0 θ_0 θ0和 θ 1 θ_1 θ1的值是同步进行的,在每次循环中,我们只要保存 θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) θ_j-α\\frac∂∂θ_jJ(θ_0,θ_1) θj−α∂θj∂J(θ0,θ1)的值,赋值给 θ 0 θ_0 θ0和 θ 1 θ_1 θ1即可,如下:
t e m p 0 : = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) temp0:=θ_0-α\\frac∂∂θ_0J(θ_0,θ_1) temp0:=θ0−α∂θ0∂J(θ0,θ1)
t e m p 1 : = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) temp1:=θ_1-α\\frac∂∂θ_1J(θ_0,θ_1) temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ 0 : = t e m p 0 θ_0:=temp0 θ0:=temp0
θ 1 : = t e m p 1 θ_1:=temp1 θ1:=temp1
好了,现在我们来解释一下导数项 ∂ ∂ θ j J ( θ 0 , θ 1 ) \\frac∂∂θ_jJ(θ_0,θ_1) 以上是关于机器学习梯度下降与正规方程(附例题代码)的主要内容,如果未能解决你的问题,请参考以下文章