HYSBZ 2440 完全平方数(莫比乌斯反演)

Posted 2020-07-07

链接：http://www.lydsy.com/JudgeOnline/problem.php?id=2440

 

若i为质数，n为i*i的倍数，则称n为含平方因子数。

求1~n的无平方因子数。

 

F(x)为1~x的平方因子数数量，则由容斥原理及莫比乌斯函数知：

 

 

G(x)为1~x的无平方因子数数量，则:

 

 

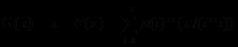
二分法枚举，注意二分法的写法。

 

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<queue>
#include<vector>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
const int N=45000;
bool vis[N];
int mu[N];
int prime[N];
void Mobius(int n){
    memset(vis,0,sizeof(vis));
    mu[1]=1;
    int tot=0;
    for(int i=2;i<=n;i++){
        if(!vis[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<tot&&i*prime[j]<=n;j++){
            vis[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

LL getNum(int n){
    int e = (int)sqrt(n);
    LL ans = 0;
    for(LL i = 1; i <= e; i++){
        ans += mu[i] * (LL)(n/(i * i));
    }
    return ans;
}
int main(){
    Mobius(N - 2);
    int t, k;
    scanf("%d", &t);
    while(t--){
        scanf("%d", &k);
        LL l = 1, r = 2 * k + 1;
        while(l < r){
            LL mid = (l + r)/2;
            if(getNum(mid) < k){
                l = mid + 1;
            }else{
                r = mid;
            }
        }
        printf("%lld\\n", l);
    }
    return 0;
}