CF#462 div1 D：A Creative Cutout

Posted 2020-10-24 GuessYCB

CF#462 div1 D：A Creative Cutout

CF#462 div1 D：A Creative Cutout

题目大意：

原网址戳我！
题目大意：
在网格上任选一个点作为圆中心，然后以其为圆心画\\(m\\)个圆。
其中第\\(k\\)个圆的半径为\\(\\sqrt{k}\\),\\(m\\)个圆的编号依次为\\(1\\)~\\(m\\)。
定义一个格点的美妙值\\(g(x,y)\\)为包含了它的所有圆的编号之和。
定义\\(f(n)\\)为：当画了\\(n\\)个圆时，\\(f(n) = \\sum_{i,j\\in R} g(i,j)\\)。
现在非常变态的问你一个非常无聊的恶心问题：
给定一个\\(m\\)(\\(m\\leq 10^{12}\\))，请计算\\(ans = \\sum_{i = 1}^m f(i)\\ mod\\ 1000000007\\)

样例与样例解释

样例输入输出
\\(Input\\)：5
\\(Output\\)：387

样例说明：
样例中，当\\(n = 5\\)时圆的分布情况如下图所示：

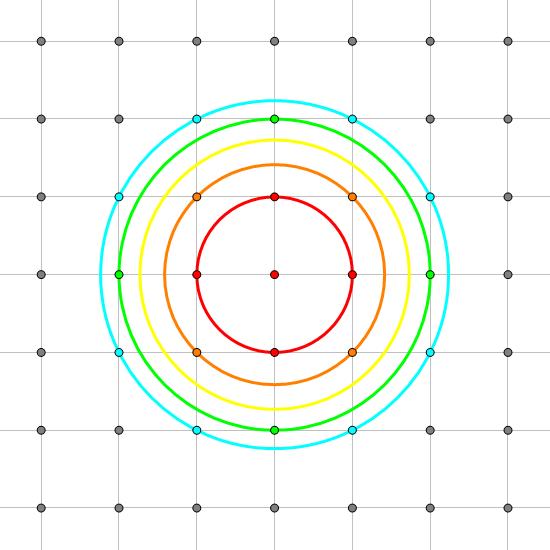
当\\(n = 5\\)时，如图
有\\(5\\)个红色的点被圆1、2、3、4、5包含 ， 它们的\\(r = \\sum_{i = 1}^5 i = 15\\)
有\\(4\\)个橘色的点被圆2、3、4、5包含，它们的\\(r = \\sum_{i = 2}^5 i = 14\\)
有\\(4\\)个绿色的点被圆4、5包含，它们的\\(r = \\sum_{i = 4}^5 i = 9\\)
有\\(8\\)个蓝色的点被圆5包含 ， 它们的\\(r = 5\\)
剩下的灰色的点则不被任意一个圆包含，它们的\\(r = 0\\)
综上，\\(f(5) = 5\\times 15 + 4\\times 14 + 4\\times 9 + 8\\times 5 = 207\\)
同理可得\\(f(1)\\)=\\(5\\)、\\(f(2)\\)=\\(23\\)、\\(f(3)\\)=\\(50\\)、\\(f(4)\\)=\\(102\\)。
所以当\\(m = 5\\)时 ， \\(ans = \\sum_{i = 1}^5 f(i) = 5+23+50+102+207 = 387\\)

解法与思路

这TM比 \\(E\\)题 还要难好多好吗？
这里方便叙述我们以圆心为原点建立坐标轴。
对于一个\\(f(n)\\)，我们可以计算出每一个坐标的贡献：
\\(res_n = \\sum_{k = x^2 + y^2} ^ n k = \\frac{(n+(x^2+y^2))(n-(x^2+y^2)+1)}{2}=\\frac{n(n+1) - (x^2+y^2)(x^2+y^2-1)}{2}\\)
转换一下得到：\\(res = \\binom{n+1}{2} - \\binom{x^2+y^2}{2}\\)
令\\(L = x^2 + y^2\\)，则每一个\\(L\\)的答案的贡献为：
\\(Res_L = \\sum_{k = L}^m (\\binom{k+1}{2} - \\binom{x^2+y^2}{2}) = \\sum_{k = L}^m \\binom{k+1}{2} - (m - L +1)\\binom{L}{2}\\)
然后这里有一个组合公式( 提示 )：

公式：\\(\\sum_{k = L}^R \\binom{k}{w} = \\binom{R+1}{w+1} - \\binom{L}{w+1}\\)
用归纳法证明：
当\\(L = R = 1\\)时，\\(\\sum_{k=1}^1\\binom{1}{1} = \\binom{2}{2} - \\binom{1}{2} = 1\\)成立。
\\(\\sum_{k = L}^{R+1}\\binom{k}{w} = \\binom{R+1}{w}+\\sum_{k=L}^R\\binom{k}{w} = [\\binom{R+1}{w+1}+ \\binom{R+1}{w}] - \\binom{L}{w+1}\\)
由组合数的计算公式可得\\(\\binom{R+1}{w+1}+ \\binom{R+1}{w} = \\binom{R+2}{w+1}\\)
所以\\(\\sum_{k = L}^{R+1} \\binom{k}{w} = \\binom{R+2}{w+1} - \\binom{L}{w+1}\\)依旧成立。
同理可以证明\\(L\\)变化到\\(L+1\\)此结论任符合。
综上：\\(\\sum_{k = L}^R \\binom{k}{w} = \\binom{R+1}{w+1} - \\binom{L}{w+1}\\)

我们套用这个公式：
\\(Res_L = \\binom{m+2}{3} - \\binom{L+1}{3} - (m-L+1)\\binom{L}{2}\\)
\\(Res_L = \\frac{1}{6}(\\frac{(m+2)!}{(m-1)!} - \\frac{(L+1)!}{(L-2)!} - (m-L+1)\\frac{3L!}{(L-2)!})\\)
暴力化简一顿之后得到：

\\[Res_L = \\frac{1}{6}[\\ 2L^3-3(m+2)L^2+(3m+4)L+m(m+1)(m+2)\\ ] \\]

嗯，一个关于\\(L\\)的多项式。
考虑一下枚举\\(x^2\\) 与 \\(y^2\\)的话：
令\\(L = x^2 + y^2\\)的话，带入原式中可以得到：
\\(Res_L = \\frac{1}{6}(\\)
\\(\\ \\ \\ \\ \\ 2*y^6+\\)
\\(\\ \\ \\ \\ (6x^2-(3m+6))*y^4+\\)
\\(\\ \\ \\ \\ (6x^4-2(3m+6)x^2+(3m+4))*y^2+\\)
\\(\\ \\ \\ \\ (2x^6-(3m+6)x^4+(3m+4)x^2+(m)(m+1)(m+2))*y^0\\)
\\()\\)
等于说，我们如果枚举了\\(x\\)，那么上面除\\(y\\)以外其它的都是系数(常数)。
我们把它命名为一个关于\\(y\\)的函数\\(S_x(y)\\)，那么答案可以写为：

\\[Ans = \\frac{1}{6}\\sum_{x \\in Z }^{x^2 \\leq m}\\ \\sum_{y\\in Z}^{y^2 \\leq m - x^2} S_x(y) \\]

所以说，我们只需要枚举\\(x\\)，然后计算\\(\\sum_{y\\in Z}^{y^2 \\leq m - x^2} S_x(y)\\)即可。
而\\(S_x(y)\\)中，我们只需要计算\\(y^2\\)、\\(y^4\\)、\\(y^6\\)即可。
然后对于上面这三项，我们单独算答案，可以直接套数学公式：

\\(\\sum_{i=1}^{N}i^{2}=\\frac{N(N+1)(2N+1)}{6}\\)
\\(\\sum_{i=1}^{N}i^{4}=\\frac{N(N+1)(2N+1)(3N^2+3N-1)}{30}\\)
\\(\\sum_{i=1}^{N}i^{6}=\\frac{N(N+1)(2N+1)(3N^4+6N^3-3N+1)}{42}\\)
求\\(\\sum_{i=1}^N i^{2t}\\)的\\(O(1)\\)公式，用\\((r+1)^{2t+1} - r^{2t+1}\\)变形即可得到。

枚举\\(x\\)只需要枚举\\(\\sqrt{m}\\)次，所以总的复杂度为\\(O(\\sqrt{m})\\)。

实现代码：

注意不要暴\\(int64\\)了!!
枚举\\(x\\)直接从\\(-\\sqrt{m}\\)枚举到\\(\\sqrt{m}\\)即可，省去讨论的麻烦。

#include<bits/stdc++.h>
#define ll long long
#define MOD 1000000007
using namespace std;
ll mod(ll e){ e %= MOD; if(e < 0)e += MOD; return e; }

ll inv6 , inv30 , inv42;
ll f[5] , n , m , x , y , x2 , x4 , x6 , ans;

ll Pow(ll T , ll js , ll S){
	while(js){ if(js&1)S = mod(S * T);
	T = mod(T * T); js >>= 1; } return S;
}
ll sum(ll i , ll k){
	if(k == 0)return mod( 2*i + 1 );
	ll s0 = mod( 2 * mod( mod( i * (i+1) ) * mod(2*i + 1) ) );
	if(k == 2)return mod(inv6 * s0);
	ll t0 , t1 , t2 , t3 , t4;
	t0 = 1; t1 = i; t2 = mod(i * i); t3 = mod(t1 * t2); t4 = mod(t2 * t2);
	if(k == 4)return mod(inv30 * mod(s0 * mod( mod(3 * t2) + mod(3 * t1) - t0 )));
	if(k == 6)return mod(inv42 * mod(s0 * mod(mod(3*t4) + mod(6*t3) - mod(3*t1) + t0) ) );
}

int main(){
	ans = 0; cin >> m;  n = sqrt(m); 
	f[0] = mod( mod(mod(m) * mod(m+1)) * mod(m+2) );  //注意这里别爆int64了！
	f[1] = mod( 3*m + 4 );
	f[2] = mod( -1 * (3*m + 6) ); 
	f[3] = 2;
	inv6 = Pow(6 , MOD - 2 , 1);  
	inv30 = Pow(30 , MOD - 2 ,1);
	inv42 = Pow(42 , MOD - 2 , 1);
	for(ll x = -n; x <= n; x ++){
		y = sqrt(m - x * x);
		x2 = mod(x * x); x4 = mod(x2 * x2); x6 = mod(x2 * x4);
		ans = mod( ans + mod(f[3] * sum(y , 6)) );
		ans = mod( ans + mod( mod( mod(6 * x2) + f[2] ) * sum(y , 4) ) );
		ans = mod( ans + mod( mod(mod(6 * x4) + mod(mod(2 * f[2])*x2) + f[1]) * sum(y , 2)) );
		ans = mod( ans + mod(mod(f[3]*x6) + mod(f[2]*x4) + mod(f[1]*x2) + f[0]) * sum(y , 0) );
		ans = mod( ans );
	}
	ans = mod( ans * inv6 ); cout << ans; return 0;
}