迷宫问题的求解（广度优先搜索）

Posted 2020-10-24 yuxiaoba

     迷宫问题很容易可以理解为广度优先搜索问题，站在一个点上，首先试一试自己周围的点是否可以走，如果是路则加入待走队列，如果是墙则丢弃。迷宫问题在广度优先搜索的时候需要特别注意的就是要及时抛弃，遇到走过的点立即丢弃，遇到墙立即丢弃，不然时间复杂度就很高。

  

题目描述

Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会. 

魔王住在一个城堡里,城堡是一个A*B*C的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1. 

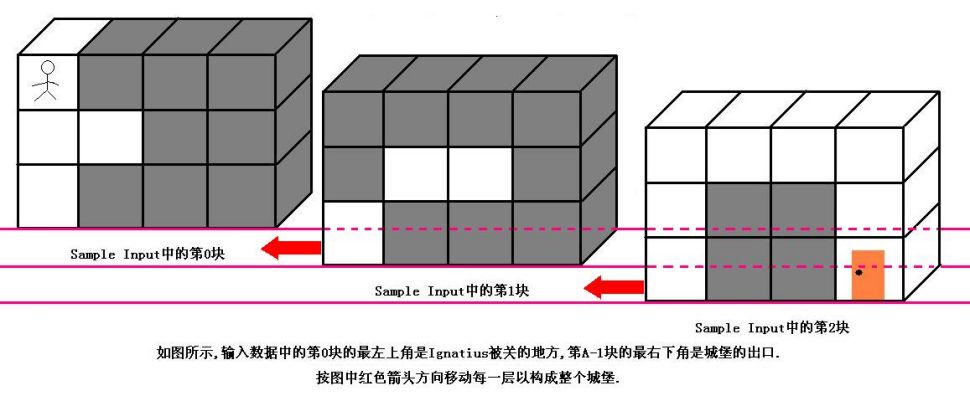<center></center>

输入描述:

输入数据的第一行是一个正整数K,表明测试数据的数量.每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表城堡的大小和魔王回来的时间.然后是A块输入数据(先是第0块,然后是第1块,第2块......),每块输入数据有B行,每行有C个正整数,代表迷宫的布局,其中0代表路,1代表墙.(如果对输入描述不清楚,可以参考Sample Input中的迷宫描述,它表示的就是上图中的迷宫)
       

特别注意:本题的测试数据非常大,请使用scanf输入,我不能保证使用cin能不超时.在本OJ上请使用Visual C++提交.
       

输出描述:

对于每组测试数据,如果Ignatius能够在魔王回来前离开城堡,那么请输出他最少需要多少分钟,否则输出-1.
       

示例1

输入

1
3 3 4 20
0 1 1 1
0 0 1 1
0 1 1 1
1 1 1 1
1 0 0 1
0 1 1 1
0 0 0 0
0 1 1 0
0 1 1 0

输出

11
这道题一开始看题看半天，其实它就是3*3*4=36个点，是一个立体的图形，下面的0，1就是表示那个点是路还是墙

 1 #include<stdio.h>
 2 #include<queue>
 3 
 4 using namespace std;
 5 
 6 bool mark[50][50][50];  //标记数组
 7 int maze[50][50][50];   //保存立方体信息
 8 
 9 struct Node
10 {
11     int x,y,z;
12     int t;
13 };
14 queue<Node> Q;
15 
16 int go[][3]
17 {
18     1,0,0,
19     -1,0,0,
20     0,1,0,
21     0,-1,0,
22     0,0,1,
23     0,0,-1
24 };
25 
26 int BFS(int a,int b,int c)
27 {
28     int i;
29     Node temp;
30     while( Q.empty()==false)
31     {
32         Node now = Q.front();
33         Q.pop();
34         for( i=0; i<6; i++)
35         {
36             //依次扩展6个相邻结点
37             int nx = now.x+go[i][0];
38             int ny = now.y+go[i][1];
39             int nz = now.z+go[i][2];
40             if( nx<0 || nx>=a || ny<0 || ny>=b || nz<0|| nz>=c)
41                 continue;  //若再立方体外则丢弃
42             if( maze[nx][ny][nz]==1)
43                 continue;  //若为墙则丢弃
44             if( mark[nx][ny][nz]==true)
45                 continue;  //若访问过则丢弃
46 
47             temp.x = nx;
48             temp.y = ny;
49             temp.z = nz;
50             temp.t = now.t+1;
51             Q.push(temp);   //新位置加入队列中
52             mark[nx][ny][nz] = true;  //标记该位置
53             if( nx==a-1 && ny==b-1 && nz==c-1)
54                 return temp.t;  //到达终点
55         }
56     }
57     return -1;
58 }
59 int main()
60 {
61     int n;
62     int i,j,k;
63     int a,b,c,t;
64     int ret;
65     scanf("%d",&n);
66     while( n--)
67     {
68 
69         scanf("%d%d%d%d",&a,&b,&c,&t);
70         for( i=0; i<a; i++)
71         {
72             for( j=0; j<b; j++)
73             {
74                 for( k=0; k<c; k++)
75                 {
76                     scanf("%d",&maze[i][j][k]);
77                     mark[i][j][k] = false;
78                 }
79             }
80         }
81         while( Q.empty()==false) Q.pop();  //清空队列
82         mark[0][0][0] = true;  //标记起点
83         Node temp;
84         temp.t = temp.x = temp.y = temp.z=0;
85         Q.push(temp);
86         ret  = BFS( a,b,c);
87         if( ret<=t) printf("%d\n",ret);   //成功逃出输出时间，无法找到终点输出-1
88         else printf("-1\n");  //若时间超过返回-1
89     }
90     return 0;
91 }