算法浅谈——走迷宫问题与广度优先搜索

Posted 2021-04-14 TechFlow

在之前周末LeetCode专栏当中，我们详细描述了深度优先搜索和回溯法，所以今天我们继续这个话题，来和大家聊聊搜索算法的另一个分支，广度优先搜索。

广度优先搜索的英文是Breadth First Search，简写为bfs。与它相对的深度优先搜索，英文自然就是Depth First Search，简写成dfs。所以如果在阅读我或者其他人的代码时发现有个函数叫做bfs或者dfs，如果你能回忆起这些英文缩写，一定可以明白它们是什么意思。

bfs与dfs

在讲解bfs的概念之前，我们先来回顾一下dfs的概念，好有个对比。

通过之前的文章，我们已经知道了实现dfs往往需要使用递归。我们在一次递归当中需要遍历当前所有的决策，然后递归去执行这些决策。如果这些决策会对未来的决策产生影响，那么我们还需要使用回溯法，在决策遍历结束之后，撤销当前的操作。

所以我们有了dfs的模板代码：

def dfs(n):
    if n > depth:
        return 
    for i in decisions:
        do_decision(i)
        dfs(n+1)
        rollback(i)

假如我们有一棵树，我们需要遍历树。显然由于树是由节点组成的树形结构，不是list结构，所以我们并不能直接用循环来遍历。为了避免重复，我们需要按照一定的顺序在树上遍历。最常用的就是使用dfs和bfs，我们先来看一下dfs怎么解决这个问题。

套用一下上面的模板，我们可以很容易写出来：

def dfs(node):
    if node is None:
        return
    for child in node.childs:
        print(child)
        dfs(child)

由于我们只需要遍历节点，遍历的过程并不会对后面的遍历产生影响，所以我们不需要rollback这一步。并且树天然有结构，我们递归的顺序刚好和树本身的顺序一致，都是从父节点往子节点遍历。所以并不需要其他的处理。

假如我们有这样一棵树：

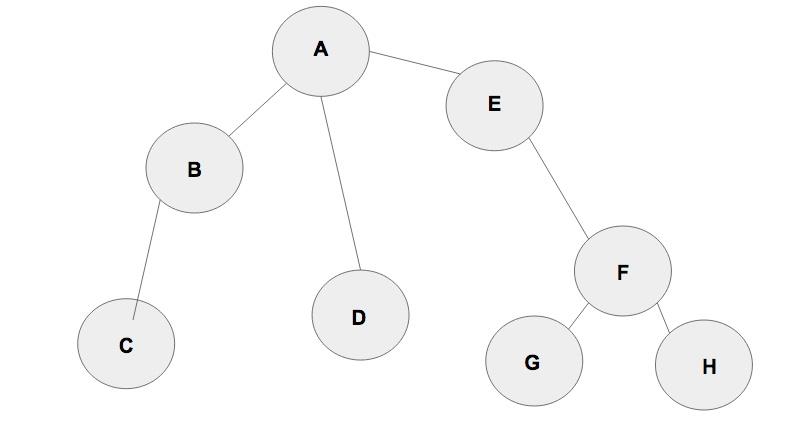
使用dfs去遍历它，得到的顺序会是什么？

稍微带入一下上面遍历的逻辑应该就能想明白，它的顺序是：A->B->C->D->E->F->G->H。

有没有看出规律？其实dfs就是先一条路走到头，然后再回头去遍历其他的路。也就是当我们面临多种决策的时候，我们优先往深度更大的方向前进。

而广度优先搜索与它的逻辑刚好相反，从字面上意思我们也应该能猜得出来，bfs在搜索的时候倾向于先把当前所有的决策都做一遍，也就是它会往广度更大的方向前进。

举一个很简单的例子，比如我们玩一个有多种结局的游戏。深度优先搜索就是不管三七二十一，先玩到通关再说，之后再来改变选择去获取其他的结局。而广度优先搜索则是在游戏面临选择的时候不停地存档，把所有可能性都遍历一便，之后再一个一个读取存档，重复这个操作。

所以回到上面那个树遍历的问题，如果是bfs，它的遍历顺序显然就是A->B->D->E->C->F->G->H。

实现方法

仔细分析会发现dfs是纵向的遍历搜索树，而bfs则是横向进行的。在实现dfs的时候，我们其实是借用了系统栈替我们存储了之前遍历的状态。而现在我们需要横向遍历的时候，显然递归就不适用了，但是我们同样需要一个数据结构来存储遍历时候的状态，就好像游戏存档一样。

再观察一下这棵树，A节点一共有3个分支B，D和E。我们通过A节点可以拿到这三个节点。之后我们要依次遍历这三个节点，拿到它们的所有分支。也就是说我们遍历这BDE三个节点的顺序就是我们遇见它的顺序，我们把存储状态认为是写入容器，而读取的时候则认为从容器中弹出，那么这个容器应该是先进先出的。

栈是先进后出的所以不满足，而队列是先进先出的，这正是我们需要的。所以bfs是基于队列实现的。

有了队列之后，我们就可以把维护状态的工作交给它，我们只需要关注遍历单个节点的逻辑就好了。因为队列会替我们把这些节点串起来，当队列当中没有元素的时候，就说明我们已经遍历结束了。

我们写下模板代码：

queue = Queue()
while not queue.empty():
    state = queue.front()
    queue.pop()
    print(state)
    for new_state in state.new_states():
        queue.put(new_state)

很简单对不对，使用队列之后，遍历的代码同样没有几行。关于队列，实现的方法有很多。只要掌握了原理，用什么实现都是一样的，list和链表都可以。Python当中替我们实现了队列，在Python3版本当中是queue，Python2则是Queue，这里需要注意一下。我使用的是Python3，所以就是queue，用法也很简单：

from queue import Queue
que = Queue()
while not queue.empty():
    state = queue.get()
    print(state)
    for new_state in state.new_states():
        queue.put(new_state)

观察一下就会发现，根据我的理解获取队列头部的元素和头部的元素弹出其实是两个操作。但是在queue库当中，将它们合并成了一个。也就是说我们在使用get方法获取头部元素的时候，它就自动弹出队列了，这点需要注意。大多数情况下这点并没有问题，但是有时候我们可能会希望先获取，再来判断要不要出列，这时候就不能使用这个库了，可以考虑一下双端都可以插入弹出的deque，或者是自己用list实现。

重点来了

如果大家在学习的过程当中抱着批判和求知的精神，肯定会有一个问题，就是我们为什么要发明两种遍历方法呢？我们学会bfs究竟有什么用处呢，难道dfs递归实现都不用自己维护数据结构不香吗？

这一点想想就知道非常重要，如果这点不明白，我们在实际当中遇到问题怎么知道究竟用什么算法呢？但是遗憾的是，大多数教科书上并不会涉及这点，而是留给读者自行思考，不得不说比较坑爹。

其实说起来只有一点差别，就是当我们搜索没有结束就找到答案时，bfs可以提前结束，而dfs往往不能。

提前结束这个问题其实有两个点，我们先来看其中比较简单的一个：bfs实现通常是通过while循环，而不是使用递归。那么，当我们已经找到答案的时候，我们可以很简单地通过break跳出循环，提前结束遍历。但是dfs则相对比较困难。可能有些同学会说我们也可以在递归函数里return啊，难道不是一样的么？

其实还真的不太一样，我们在递归当中执行return只能退出当前这一次执行，return之后会回到上层调用的地方，整个搜索过程并没有结束。举个例子：

def dfs(n):
    if n > 20:
      return
    print(n)
    for i in range(n+1, 50):
      dfs(i)

当n等于21的时候，会触发n > 20的条件，进行return，但是return之后会回到上一层循环的位置，后面i=21，22……50还是会执行。也就是说虽然return了，但是整个递归过程没有结束，结束的只是当前这一个节点。而如果是bfs，由于我们是在循环当中执行的遍历，我们直接break这个循环就可以结束整个bfs过程。

深入思考

如果我们只是想要搜索有没有答案，或者是只想要获得一个答案的时候，那么其实dfs和bfs是差不多的。虽然dfs会有无法直接退出的问题，但这并不是完全没有办法解决的，通过引入全局变量等方法，我们也可以变相提前退出，虽然稍微麻烦一点。

但如果我们想要寻找最优的答案，往往dfs就不适用了。

我们来看一个经典的例子，也是bfs的经典使用场景，即走迷宫问题。

###########
#  S      #
#         #
#     # # #
#     #E# #
###########

上图是一个非常简单的迷宫，s表示起点，E表示终点。#表示篱笆，也即不能走到的位置。如果我们只是询问这个迷宫是否有可行解，那么dfs和bfs都是一样的。而且从编码习惯上来说，我们可能更倾向于使用dfs来做回溯。

但如果我们想知道从起点走到终点的最短路径的话，那么这道题基本上就只能使用bfs了。

原因很简单，因为当我们通过dfs找到终点的时候，我们并不能得知它是否是最短的路径。为了找出最短路径，我们只能把所有通往终点的路径都记录下来，然后通过比较返回最短的。这显然是不科学的，因为我们额外遍历了许多不必要的状态，在一个搜索问题当中，这些不必要的状态可能是非常多的。而由于bfs是横向遍历，当找到终点的时候，就一定是最优解，所以直接break循环返回就行了，避免了大量没有必要的遍历。

也就是说能够在第一时间找到答案，和最快到达答案的路径，这个是bfs最大的特点。这也是我们在问题当中使用bfs的本质原因。

初学者往往因为对于queue不熟悉而更倾向于使用dfs，而缺乏了对于这两种搜索算法本质的理解，除了算法本身的原理，这也是非常重要的。

最后，我们附上bfs走迷宫的代码：

from queue import Queue
from collections import defaultdict

que = Queue()
directions = [[0, 1], [1, 0], [0, -1], [-1, 0]]
visited = defaultdict(bool)


def bfs(S, E, maze):

    # S is start, E is end
    # maze 地图
    # visited 记录走过的位置
    n, m = len(maze), len(maze[0])
    que.push((S, []))
    visited[S] = True
    
    while not que.empty():
        position, states = que.get()
        if position == E:
            states.append(E)
            return states
        for xi, xj in directions:
            # 拷贝，Python中list是引用传递，不使用copy会引起出错
            cur = states.copy()
            x, y = position[0] + xi, position[i] + xj
            if 0 < x < n and 0 < y < m and maze[x][y] != '#' and not visited[(x, y)]:
                visited[(x, y)] = True
                cur.append((x, y))
                que.put(((x, y), cur))
              
    return []

到这里关于bfs算法的介绍就告一段落了，在后面LeetCode专题，我们会结合具体的题目为大家介绍更多bfs的用法。感兴趣的同学可以小小期待一下。

如果觉得有所收获，请顺手点个在看或者转发吧，你们的举手之劳对我来说很重要。