走迷宫之广度优先搜索

Posted 2021-04-14 樽中月的分享

春天是走迷宫的好季节。

用深度优先搜索走完迷宫，有人会问，难道只有这一种算法吗？

当然不是啦，其实你可以用暴力试试（尽管很笨，很慢）。

还有一种方法，叫做广度优先搜索。

 

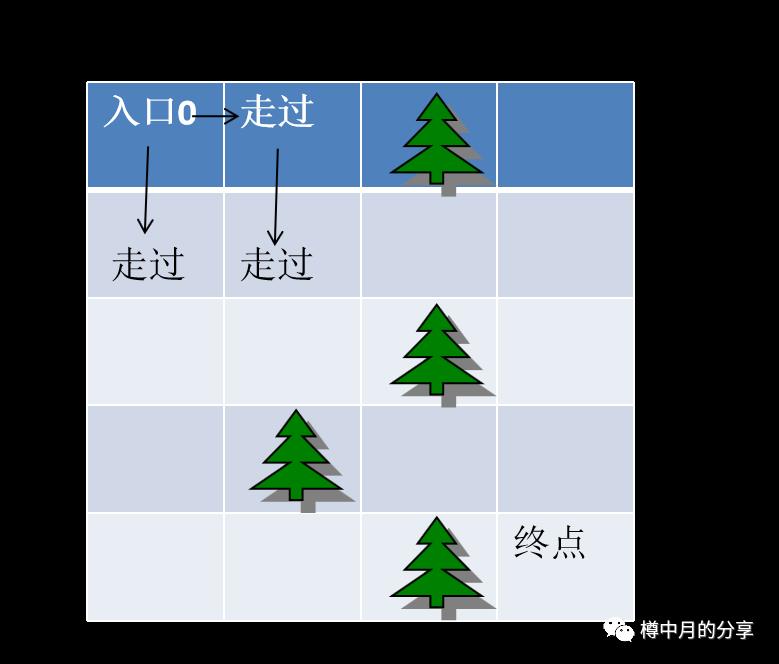
假装我们是计算机，站在迷宫的入口处。也就是下图第1行第1列的位置。

 

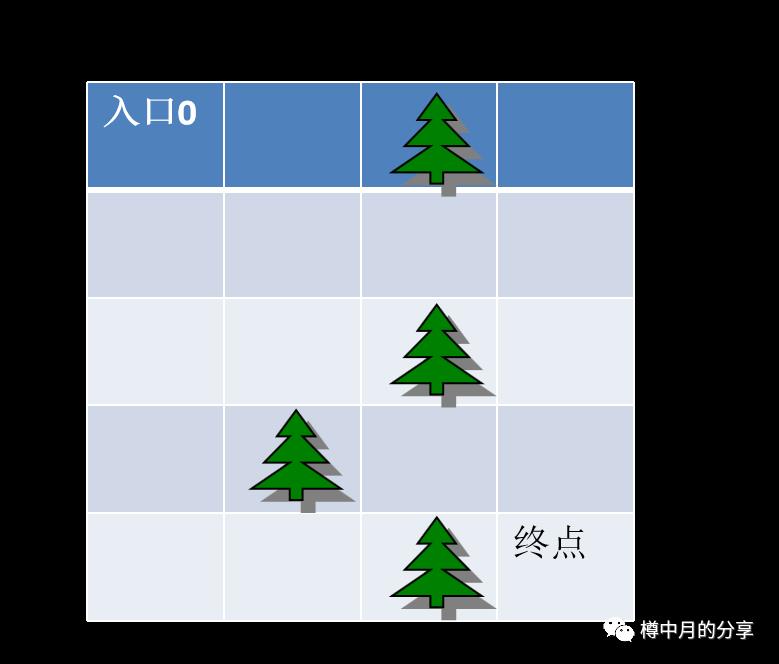
和深搜一样，按照右、下、左、上的顺序，第1个能走到的点是第1行第2列，记为：(1,2)。好，先把这个点标记为“走过”。

 

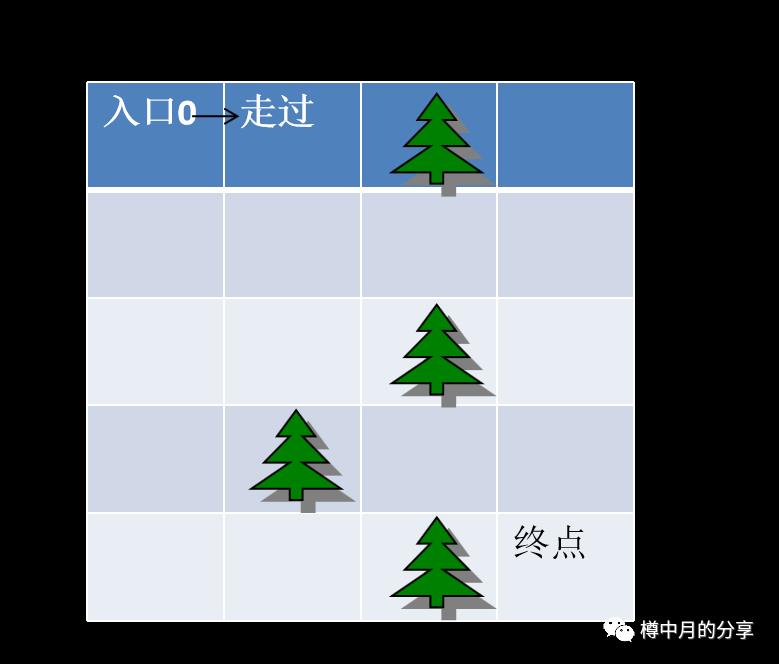
仅仅把迷宫里某个点做个“走过”标记是不够的，我们还需要标记是从哪个点走到这里的，也就是（1,1）也需要保留下来，于是有了下面这张图。我们把这张图，叫做“队列”。

 

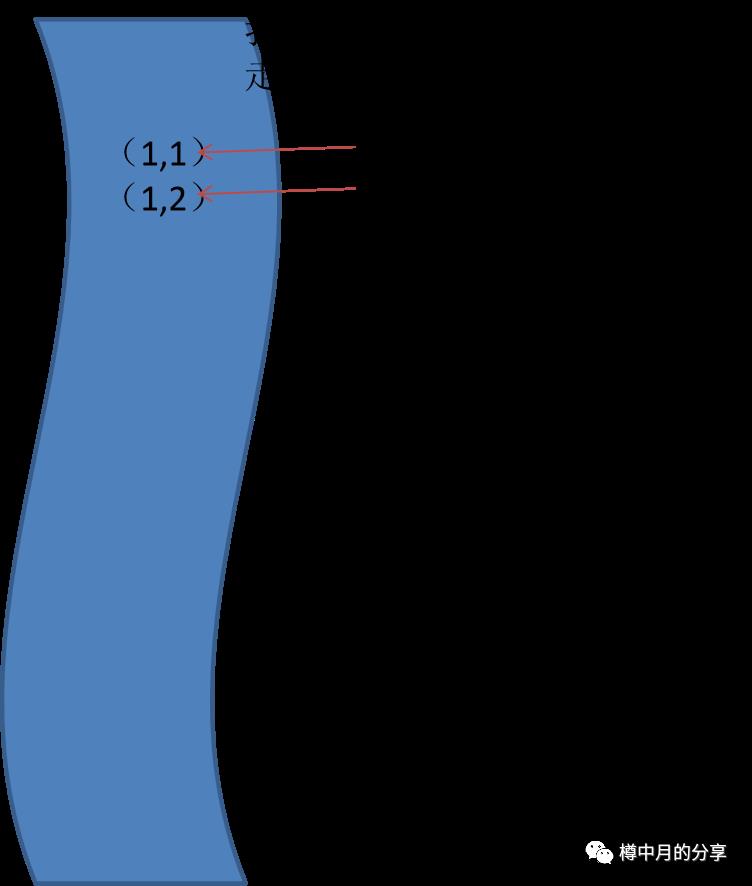
接着，我们不往下走了，从起点出发不是还有其他方向吗：起点的下方，第2行第1列。把它标记为“走过”，同时也添加到队列中。我们把某个点加入到队列中的操作，叫做“入队”。

 

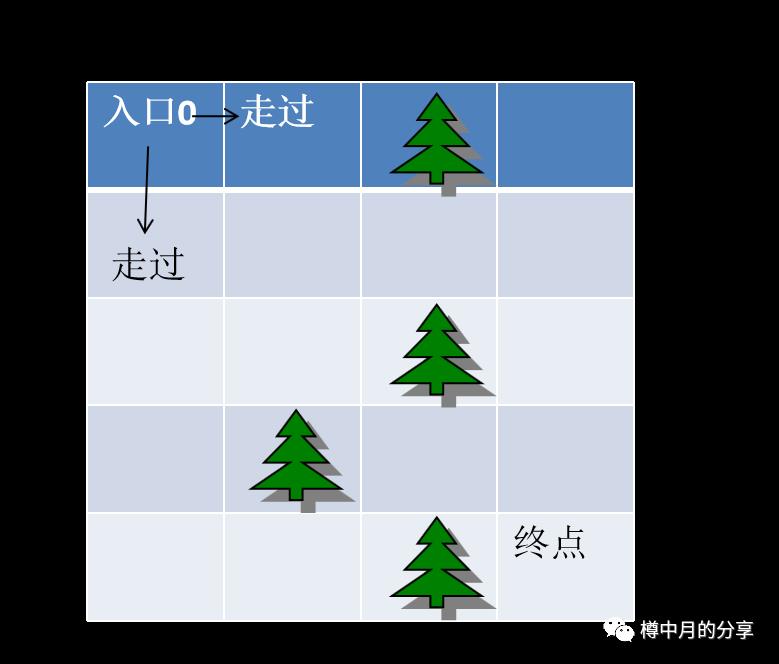
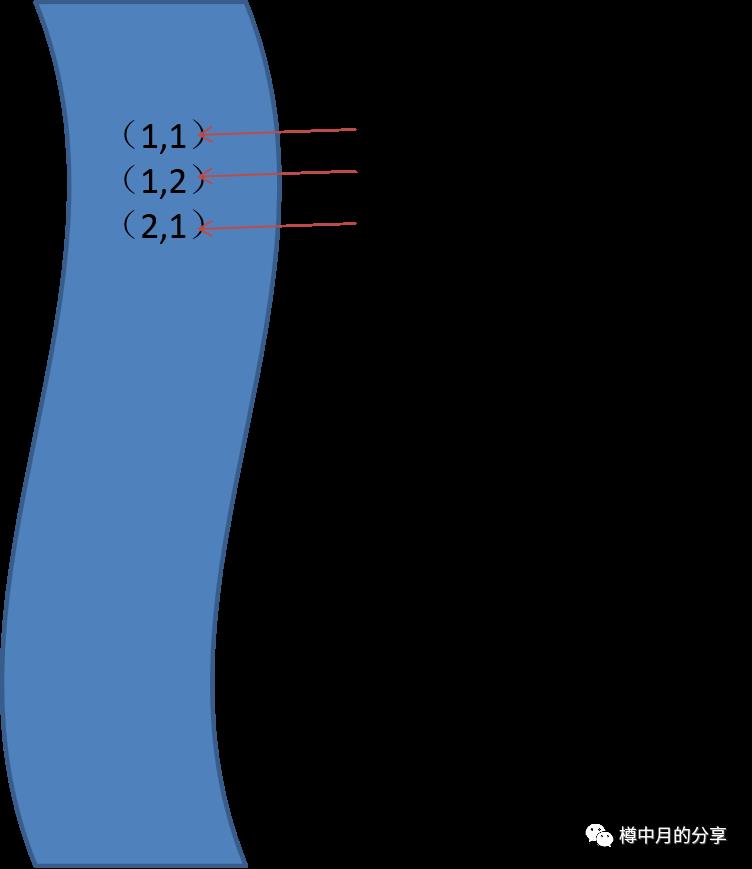
好，现在迷宫里有3个点被标记为“走过”，就是入口和它相邻的两个点；相应的，队列里有3个点，其中第一个点（就是起点）我们叫队首元素，后面那两个跟班是它能走到的两个方向的点，最后那个，叫做队尾元素。见上图。

继续换方向，从入口出发，还有其他点可以走吗？（有的话也要标记“走过”，同时入队喔。）

没有了。

也就是说，从入口出发，所有的路径已经被广度搜索完了。

既然这样，就把队列中的入口也就是点（1,1）删掉。（我们叫做：队首元素出队。）

 

 

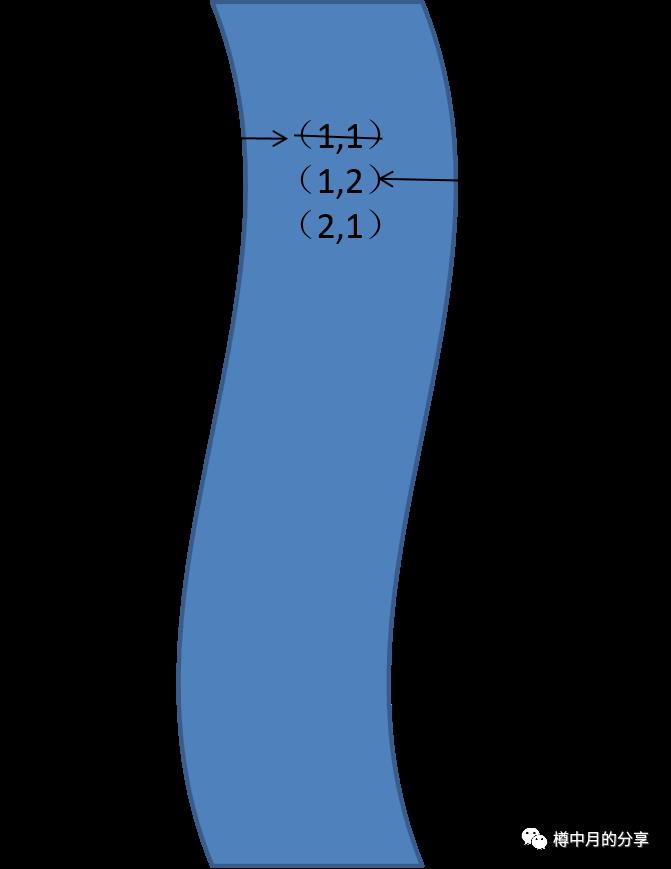
Now,从新的队首元素开始，开始新的搜索。

新的队首元素（1,2）相邻的，没有走过的点是（2,2），so被标记为“走过”，同时入队。

 

 

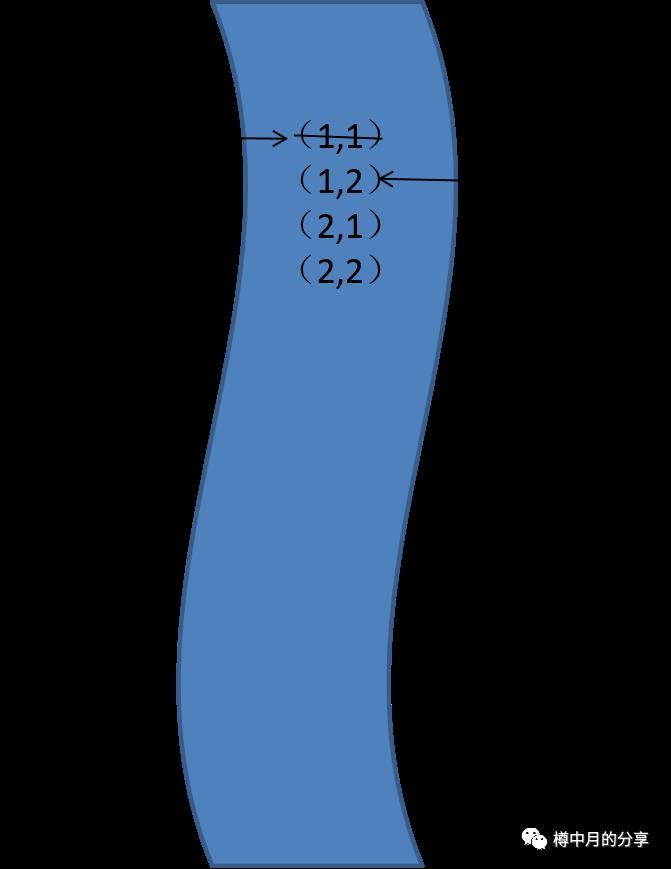
把队首元素各个方向转一遍，发现确实没有可走的点了，于是，队首元素出队，新的队首元素又产生了。

 

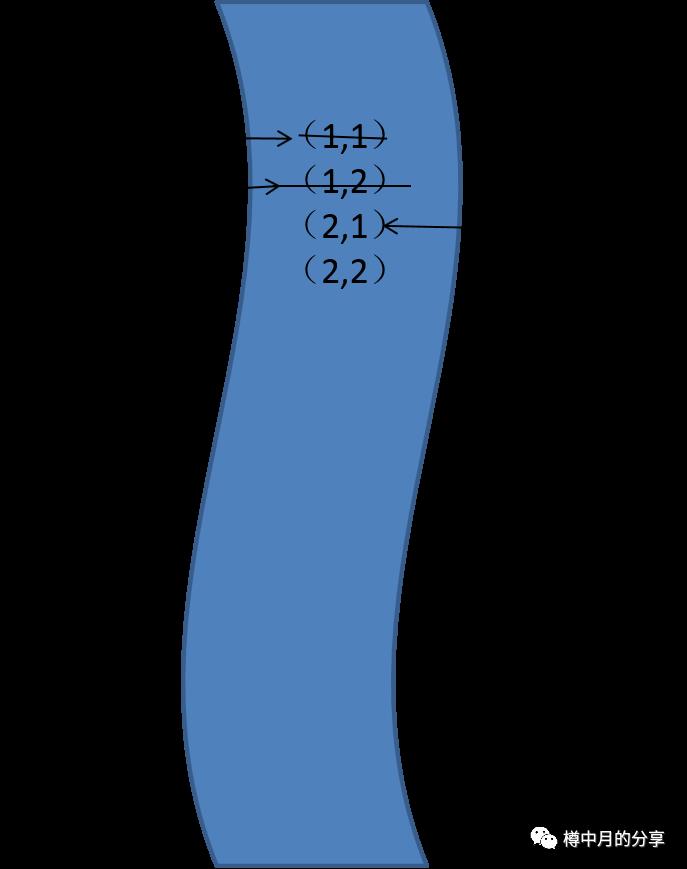
继续，搜索队首元素（2,1）相邻的点。把可以走的（3,1）标记为“走过”，同时入队。

 

 

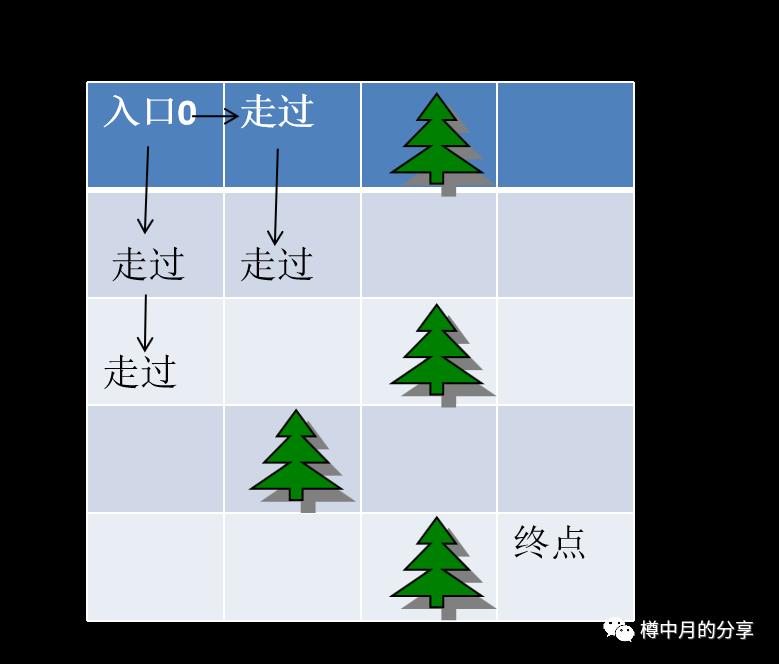
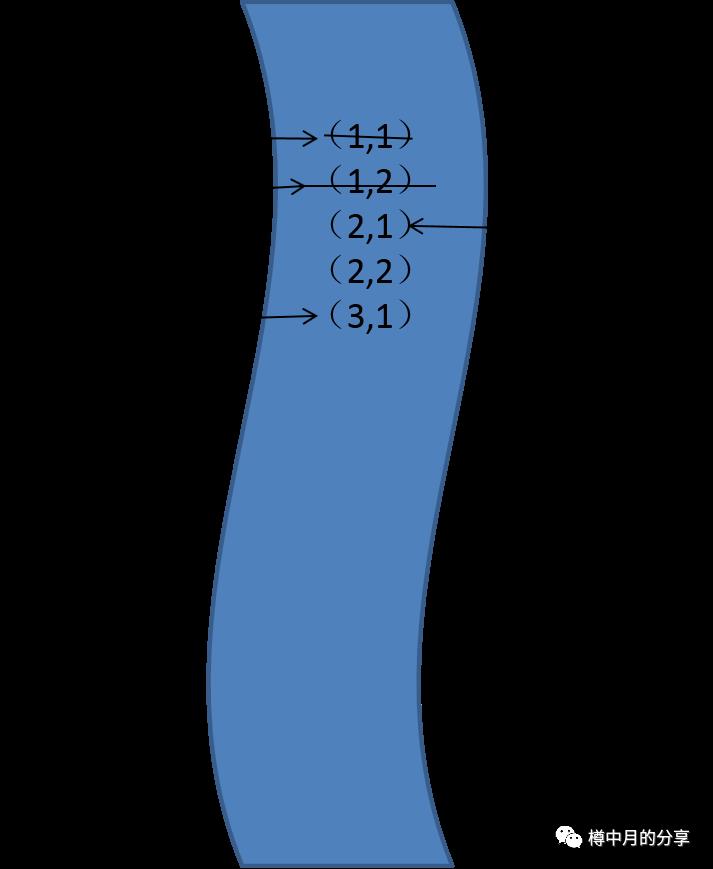
就这样重复下去：

队首元素会产生4个方向的相邻的点，如果不是障碍物，不是迷宫的边界，同时也没有被标记为“走过”时，则把这些点标记为“走过”，然后入队，当所有的方向搜完时，队首元素出队。。。一切又回到开始，直到走到终点。

这个过程如果不是计算机来做，还是非常枯燥的。

最后的标记图和队列就是下图这样子。

 

当终点（5,4）第一次出现在标记图中，同时入队时，遍历就结束了。用这种方法，虽然不能够将所有的路径都找出来，但是能够保证，它找到的路径，是最短的。

像这样，每发现一个点，就把这个点能走到的所有点都加入到一个队列中，从这个队列里找下一次要访问的点，访问过的点做标记，以后不访问，直到找到终点的方法，就是广度优先搜索（Breadth First Search）。