动态规划-石子问题

Posted 2020-10-23 TQCAI

1.直线取石子

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>


#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 100
#define MAX 1<<30
#define V vector<int>

using namespace std;

const int n=6;
int a[n]={1,5,6,7,3,2};
int sum[n];
int dp[n][n];

int getmin(){
    int i,j,v,k;
    F(v,1,n){
        FF(i,n-v){
            j=i+v;
            int tmp=sum[j]-((i>0)?sum[i-1]:0);
            dp[i][j]=MAX;
            F(k,i,j){
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+tmp);
            }
        }
    }
    return dp[0][n-1];
}

int main(){
    memset(dp,0,sizeof(dp));
    sum[0]=a[0];
    int i;
    F(i,1,n){
        sum[i]=sum[i-1]+a[i];
    }
    printf("%d\\n",getmin());
    return 0;
}

View Code

ｉ：开始下标

ｊ：结束下标

ｋ：区间下标，在【ｉ，ｊ）区间进行循环

---

2.圆形取石子

我按照直线取石子的方法在OJ：https://www.luogu.org/problemnew/show/P1880 中无法AC，然后研读了博客 http://blog.csdn.net/acdreamers/article/details/18039073 的代码：

博客代码：

#include <iostream>  
#include <string.h>  
#include <stdio.h>  
  
using namespace std;  
const int INF = 1 << 30;  
const int N = 205;  
  
int mins[N][N];  
int maxs[N][N];  
int sum[N],a[N];  
int minval,maxval;  
int n;  
  
int getsum(int i,int j)  //[i,i+j]
{                        //[i,n-1]      +   [0, (i+j)%n) ]
    if(i+j >= n) return getsum(i,n-i-1) + getsum(0,(i+j)%n);  
    else return sum[i+j] - (i>0 ? sum[i-1]:0);  
}  
  
void Work(int a[],int n)  
{  
    for(int i=0;i<n;i++)  
        mins[i][0] = maxs[i][0] = 0;  
    for(int j=1;j<n;j++)  
    {  
        for(int i=0;i<n;i++)  
        {  
            int s=i,e=i+j;
            int delta=getsum(i,j);//sum∈[i , i+j ]
            mins[i][j] = INF;  
            maxs[i][j] = 0;  
            for(int k=0;k<j;k++)  //在取石子数目上进行优化
            {  
                mins[i][j] = min(mins[i][j],
                    //从i开始，取k颗    从i+k+1开始，取j-k-1颗
                    mins[i][k] + mins[(i+k+1)%n][j-k-1] + delta);  
                maxs[i][j] = max(maxs[i][j],
                    maxs[i][k] + maxs[(i+k+1)%n][j-k-1] + delta);  
            }  
        }  
    }  
    minval = mins[0][n-1];  
    maxval = maxs[0][n-1];  
    for(int i=0;i<n;i++)  
    {  
        minval = min(minval,mins[i][n-1]);  
        maxval = max(maxval,maxs[i][n-1]);  
    }  
}  
  
int main()  
{  
    freopen("D:/CbWorkspace/动态规划/石子合并.txt","r",stdin);
    while(scanf("%d",&n)!=EOF)  
    {  
        for(int i=0;i<n;i++)  
            scanf("%d",&a[i]);  
        sum[0] = a[0];  
        for(int i=1;i<n;i++)  
            sum[i] = sum[i-1] + a[i];  
        Work(a,n);  
        printf("%d %d\\n",minval,maxval);  
    }  
    return 0;  
}  

View Code

循环情况：

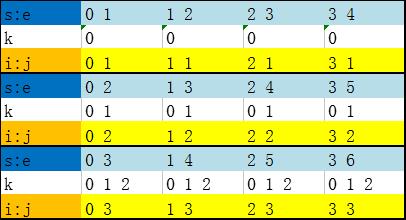
下标含义：

ｉ：取石子的开始下标【０，ｎ）

ｊ：取多少颗石子【１，ｎ）

ｋ：区间下标，在当前去ｊ颗石子之内循环　，ｋ∈【０，ｊ）

　　由ｋ切割为了两个区间：【ｉ，ｋ】和【ｉ＋ｋ＋１，ｊ－ｋ－１】

　　含义为：区间①为从ｉ开始，取了ｋ颗石子。区间②为从区间①结束得地方（ｉ＋ｋ＋１）取剩下的石子（ｊ－ｋ－１）。

　　加起来一共取了ｊ－１颗。

对于ｋ的实例分析：

●ｊ＝１时（取１颗），ｋ＝０，

　　划分为两个区间：①【０,０】，②【１,０】，这两个区间的ｄｐ值都是０　。然后加上ｓｕｍ（ｉ，ｉ＋ｊ），得到了正确的值

●ｊ＝２时，ｋ＝０～１，

　　ｋ＝０时，①【０,０】，②【１,１】，用ｓ＝ｉ，ｅ＝ｉ＋ｊ还原：【０,０】，【１,２】

　　ｋ＝１时，①【０,１】，②【２,０】，　　　　　～　　　　　　：【０,１】，【２,２】

注：以上分析都没有用“取模运算”来对下标进行重定位

理解后我的编码（主代码）：

    int i,j,k;
    I("%d",&n);
    F(i,0,n){
        I("%d",&a[i]);
    }
    sum[0] =a[0];
    F(i,1,n) sum[i]=a[i]+sum[i-1];
    F(j,1,n){                                //开始下标 
        F(i,0,n){                            //取石子数目
            int delta=getsum(i,i+j);    　　　//区间[i,i+j]的 和 
            mins[i][j]=MAX;                  //初始化mins 
            F(k,0,j){                        //区间下标 
                mins[i][j]=min(mins[i][j],
                               mins[i][k] + mins[(i+k+1)%n][j-k-1]+delta) ;
                maxs[i][j]=max(maxs[i][j],
                               maxs[i][k] + maxs[(i+k+1)%n][j-k-1]+delta) ;
            } 
        } 
    }
    //计算完毕，找出最后的最大值和最小值
    F(i,0,n){
        max_ans=max(max_ans,maxs[i][n-1]);
        min_ans=min(min_ans,mins[i][n-1]);
    } 
    O("%d\\n%d\\n",min_ans,max_ans);

完整代码：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>

#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 300
#define MAX 1<<30
#define V vector<int>

using namespace std;

int a[LEN];
int sum[LEN];
int maxs[LEN][LEN];
int mins[LEN][LEN];
int max_ans=0;
int min_ans=MAX;
int n;

int getsum(int i,int j){
    if(j>=n){
        return getsum(i,n-1) + getsum(0,j%n);
    }else{
        return sum[j] - ( i>0 ? sum[i-1] : 0 );
    }
}

int main(){
//    freopen("D:/CbWorkspace/动态规划/石子合并.txt","r",stdin);
    int i,j,k;
    I("%d",&n);
    F(i,0,n){
        I("%d",&a[i]);
    }
    sum[0] =a[0];
    F(i,1,n) sum[i]=a[i]+sum[i-1];
    F(j,1,n){                                //开始下标 
        F(i,0,n){                            //取石子数目
            int delta=getsum(i,i+j);    //区间[i,i+j]的 和 
            mins[i][j]=MAX;                    //初始化mins 
            F(k,0,j){                        //区间下标 
                mins[i][j]=min(mins[i][j],
                               mins[i][k] + mins[(i+k+1)%n][j-k-1]+delta) ;
                maxs[i][j]=max(maxs[i][j],
                               maxs[i][k] + maxs[(i+k+1)%n][j-k-1]+delta) ;
            } 
        } 
    }
    //计算完毕，找出最后的最大值和最小值
    F(i,0,n){
        max_ans=max(max_ans,maxs[i][n-1]);
        min_ans=min(min_ans,mins[i][n-1]);
    } 
    O("%d\\n%d\\n",min_ans,max_ans);
    return 0;
}

View Code