POJ 1949 Chores(DAG上的最长路 ， DP)

Posted 2020-10-22 Neord

题意：

给定n项任务， 每项任务的完成用时t和完成每项任务前需要的k项任务， 求把所有任务完成的最短时间，有当前时间多项任务都可完成， 那么可以同时进行。

分析：

这题关键就是每项任务都会有先决条件， 要完成该项任务a必须先完成他的先决条件。

所以对于每个先决条件， 我们构建一条有向边到任务本身， 然后因为要求一个最小值， 按照最长路的方式松弛（dis[v] >= dis[u] + d， u是v的先决条件， d是v的完成时间，我们以边的终点完成时间作为边的权）， 遇到没有出度的边记录答案。

方法一：最长路（2016ms）

#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#include<string>
#include<map>
#include<stack>
#include<vector>
#include<algorithm>
#include<cmath>
#define rep(i,a,b) for(int i = a; i < b; i++)
#define _rep(i,a,b) for(int i = a; i <= b; i++)
using namespace std;
const int inf = 1e9 + 7;
const int maxn = 10000 + 7;
int n, m;
vector<int> G[maxn];
int d[maxn]; //每条边以终点时间作为权值
int dis[maxn], vis[maxn];
int spfa(){
    int ans = -inf;
    fill(dis, dis+maxn, -inf); //求最长路
    queue<int> q;
    dis[0] = 0;
    q.push(0);//0点入队
    vis[0] = 1;
    while(!q.empty()){
        int u = q.front();
        for(int i = 0; i < G[u].size(); i++){
            int v = G[u][i];

            if(dis[v] < dis[u] + d[v]){
                dis[v] = dis[u] + d[v];//每条边以终点时间作为权值
                if(G[v].size() == 0) {//如果没有出边， 说明它不会对后面有任何影响， 它可能就是答案之一
                    ans = max(dis[v], ans);//直接更新答案
                    continue;
                }
                if(!vis[v]){
                    vis[v] = 1;
                    q.push(v);
                }
            }
        }
        vis[u] = 0;
        q.pop();
    }
    return ans;
}
int main()
{
    scanf("%d", &n);
    _rep(i,1,n){
        scanf("%d", &d[i]);
        int k, v;
        scanf("%d", &k);
        if(k == 0){
            G[0].push_back(i);//假设有一个0点连向所有入度为0的点， 方便处理
        }else{
            rep(j,0,k){
                scanf("%d", &v);
                G[v].push_back(i);
            }
        }
    }
    printf("%d\\n",spfa() );
}

方法二 DP（344ms）

那么我们可以转化一下，假设该项任务有k项先决条件

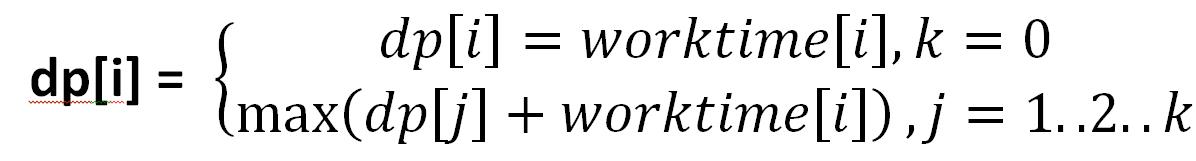
dp[i]代表完成该项任务的最早时间， 最后找出最大的dp[i]就是答案。

#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#include<string>
#include<map>
#include<stack>
#include<vector>
#include<algorithm>
#include<cmath>
#define rep(i,a,b) for(int i = a; i < b; i++)
#define _rep(i,a,b) for(int i = a; i <= b; i++)
using namespace std;
const int inf = 1e9 + 7;
const int maxn = 10000 + 7;
int worktime[maxn], dp[maxn];
int n, m;
int main()
{
//    freopen("1.txt","r", stdin);
    scanf("%d", &n);
    int ans = -inf;
    _rep(i,1,n){
        scanf("%d", &worktime[i]);//工作时间
        int k, v;
        scanf("%d", &k);
        if(k == 0){
            dp[i] = worktime[i];
        }else{
            rep(j,0,k){
                scanf("%d", &v);
                dp[i] = max(dp[i] , dp[v] + worktime[i]);//找出最晚的先决条件
            }
        }
        ans = max(ans, dp[i]);
    }
    printf("%d\\n", ans );
}