1.售票
【问题描述】
C 市火车站最近出现了一种新式自动售票机。买票时,乘客要先在售票机上输入终点名称。一共有 N 处目的地,随着乘客按顺序输入终点名称的每个字母, 候选终点站数目会逐渐减少。在自动售票机屏幕上,有一个 4 行 8 列的键盘,如下图所示。
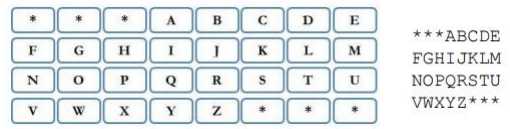
在乘客每输入一个字母后,键盘上只有有效字符是可选的(取决于还有哪些 候选终点站),其余的字母会被字符 ‘*‘ 取代。 告诉你 N 处目的地的名称,以及乘客已经输入的若干字符,请你输出键盘目前的状态。
【输入文件】
输入文件名为 kartomat.in。 第一行为一个整数 N(1 ≤ N ≤ 50)。接下来 N 行,每行一个由大写英文字母 组成的长度不超过 100 的字符串,表示一处目的地。最后一行,一个长度不超过 100 的字符串,表示按顺序输入的若干字符。
【输出文件】
输出文件名为 kartomat.out。 输出 4 行,每行一个长度为 8 的字符串,表示键盘状态。
【输入样例】
4
ZAGREB
SISAK
ZADAR
ZABOK
ZA
【输出样例】
****B*D*
*G******
********
********
【样例解释】
输入 ZA 以后,下一个字符可能是 G(终点站有可能是 ZAGREB),或 D(终点 站有可能是 ZADAR),或 B(终点站有可能是 ZABOK)。
很明显是签到题。。。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n,len,lenp; char p[51][101],in[101]; bool ans[27]; int main(){ freopen("kartomat.in","r",stdin); freopen("kartomat.out","w",stdout); scanf("%d",&n); int i,j; for(i=1;i<=n;i++) scanf("%s",p[i]); scanf("%s",in); len=strlen(in); for(i=1;i<=n;i++){ if(len>=strlen(p[i])) continue; bool ok=1; for(j=0;j<len;j++) if(in[j]!=p[i][j]){ok=0; break;} if(ok) ans[p[i][j]-‘A‘]=1; } printf("***"); int lj=3; for(i=0;i<26;i++){ if(!ans[i]) putchar(‘*‘); else putchar(i+‘A‘); if(++lj>=8){lj=0; putchar(‘\\n‘);} } printf("***"); return 0; }
2.数字
【问题描述】
有一天,Mirko 在一张纸上写了 N 个实数,然后在另一张纸上写下了这些实 数的所有整数倍中数值在区间 [A, B] 范围内的所有数(经过去重)。 第二天,Mirko 发现找不到写着 N 个实数的那张纸了,而只剩下另一张纸。 请你帮助 Mirko 还原原本的 N 个实数。 注意:本题有 Special Judge。
【输入文件】
输入文件名为 rekons.in。 第一行是一个整数 K,表示剩下的那张纸上共有 K 个实数。 第二行是两个整数 A 和 B。 接下来 K 行,每行一个实数,表示纸上的 K 个实数。实数已经去重,按递增 顺序给出。所有实数至多有 5 位小数。
【输出文件】
输出文件名为 rekons.out。 输出 N 行,每行一个实数,表示一组解。数据保证有解。如果有多组解,输 出 N 最小的;若还是有多组解,输出任意一组均可。
【输入样例 1】
4
1 2
1
1.4
1.5
2
【输出样例 1】
0.5
0.7
【输入样例 2】
5
10 25
12
13.5
18
20.25
24
【输出样例 2】
6.0
6.75
【数据规模和约定】
30%的测试数据:K ≤ 12。
50%的测试数据:输入的 K 个实数都是整数。
100%的测试数据:1 ≤ K ≤ 50,1 ≤ A < B ≤ 106。
3.词韵
【问题描述】
Adrian 很喜欢诗歌中的韵。他认为,两个单词押韵当且仅当它们的最长公共 后缀的长度至少是其中较长单词的长度减一。也就是说,单词 A 与单词 B 押韵 当且仅当 LCS(A, B) ≥ max(|A|, |B|) – 1。(其中 LCS 是最长公共后缀 longest common suffix 的缩写) 现在,Adrian 得到了 N 个单词。他想从中选出尽可能多的单词,要求它们能 组成一个单词序列,使得单词序列中任何两个相邻单词是押韵的。
【输入文件】
输入文件名为 rima.in。 第一行是一个整数 N。 接下来 N 行,每行一个由小写英文字母组成的字符串,表示每个单词。所有单词互不相同。
【输出文件】
输出文件名为 rima.out。 输出一行,为一个整数,表示最长单词序列的长度。
【输入样例】
5
ask
psk
k
krafna
sk
【输出样例】
4
【样例解释】
一种最长单词序列是 ask-psk-sk-k。
【数据规模和约定】
30%的测试数据:1 ≤ N ≤ 20,所有单词长度之和不超过 3 000。
100%的测试数据:1 ≤ N ≤ 500 000,所有单词长度之和不超过 3 000 000。
正解:trie树+树上dp
这是一道典型的字符串题。题目中提到的“押韵”都指的是后缀。我们可以把所有字符串反转过来,然后这些字符串就变成判断前缀是否满足“押韵”了。这时就可以想到把这些字符串插入一棵trie树,很明显对于一个单词节点,它只能和它的父亲节点、兄弟节点、儿子节点所表示的字符串押韵。
这么多状态转移,就是一个树上dp问题了:
设f[i]表示以节点 i 的儿子为根的子树中最长押韵序列,g[i]为次长押韵序列。
f[i]=f[j]+j.sons,其中j为拥有最长押韵序列的一个儿子。
g[i]=f[k]+k.sons,其中k为拥有次长押韵序列的一个儿子。
最后加上i的其他儿子(即i的儿子的兄弟)。
为了适应dp,我们从下往上做树上dp,也就是说用儿子节点和兄弟节点更新父亲节点咯,综合起来就上面说的三种情况。
以i为根的子树中形成的最长押韵序列长度ans=max(f[i]+g[i]+i.sons-2+(i是否带有结束标记?1 : 0)) //结束标记即单词节点
4.八维
【问题描述】
我们将一个 M 行 N 列的字符矩阵无限复制,可以得到一个无限字符矩阵。 例如,对于以下矩阵,

可以无限复制出矩阵
 。
。
我们认为矩阵是八连通的。八连通,指矩阵中的每个位置与上下左右和四个斜向(左上、右上、左下、右下)的位置相邻。因此,从矩阵任意位置出发沿八 个方向中的任意一个都可以无限延长。 如果我们随机选择一个位置和一个方向,则可以从此位置开始沿此方向连续 选取 K 个字符组成一个字符串。问,两次这样操作得到两个相同字符串的概率是 多少。(假设随机选择时任意位置是等可能的,任意方向也是等可能的)
【输入文件】 输入文件名为 osm.in。 第一行是三个整数 M,N,K。 接下来 M 行,每行一个由小写英文字母组成的长度为 N 的字符串,即 M*N 的字符矩阵。保证矩阵中至少出现两种不同字符。
【输出文件】 输出文件名为 osm.out。 输出一行,为一个化简后的分数,表示概率。
【输入样例 1】
1 2 2
ab
【输出样例 1】
5/16
【输入样例 2】
3 3 10
ban
ana
nab
【输出样例 2】
2/27
【样例解释】
样例一中,一次操作共有 16 种可能,其中得到 aa 的概率是 1/8,得到 ab 的 概率是 3/8,得到 bb 的概率是 1/8,得到 ba 的概率是 3/8。两次操作结果相同的 概率是 5/16。
【数据规模和约定】
30%的测试数据:M, N ≤ 10,K ≤ 100。
50%的测试数据:M = N 。
100%的测试数据:1 ≤ M, N ≤ 500,2 ≤ K ≤ 109。