题意 : 在二维平面上给出 N 个矩形,问你所有矩形构成的图案的面积是多少(相互覆盖的地方只计算一次)
分析 :
求矩形面积并可以模拟来做,不过使用线段树来辅助做扫描线可以更高效地求解
扫描线顾名思义就是类似有一条线在二维平面上扫过去,将矩形面积并给扫出来
实现是使用线段树来模拟这个扫描的过程
第一步就是确定扫描的方向,是从左到右扫还是从上到下扫,这里以从上到下为例
第二步就是确定题目的坐标是否可能很大,如果很大意味着线段树开不了,则要进行离散化操作
由于是从上到下,我们记录每个矩形的上下两条边的一些信息
此后将不再考虑矩形,而是从上到下考虑这些横线
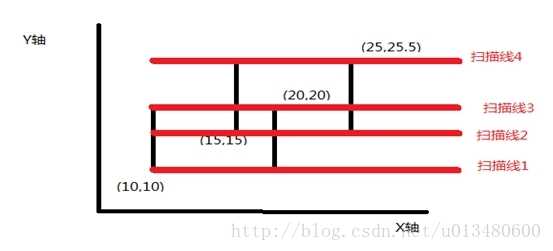
此图引用了 ==> http://blog.csdn.net/u013480600/article/details/22548393
信息包括有矩形上下两条边的左右端点的横坐标值,以及两条线的纵坐标的值即高度
然后我们给两条边的上边和下边分别做个标记,标记的作用就是判断当前矩形是要计入还是删除
在扫到当前的边为上边的时候意味着要在线段树内进行区间加法,将这条线段的值累计到线段树中
在扫到当前的边为下边的时候意味着要在线段树内进行区间减肥,将这条线段的值从线段树中删去
此时线段树在从上到下扫的过程中就一直记录着有效的横坐标值,记得刚刚我们存储的横线的高度么?
只要将有效的横坐标值(线段之长)乘以上下两条边的高度之差便得到了当前两条线段之间的面积

#include<bits/stdc++.h> #define LL long long #define lson l, m, rt<<1 #define rson m+1,r,rt<<1|1 using namespace std; const int maxn = 5e3 + 10; const int Base = 1e8; int add[maxn]; int x[maxn<<2]; long long sum[maxn<<2]; struct Node{ int flag; int l, r, h; Node(){}; Node(int L, int R, int H, int F):l(L),r(R),h(H),flag(F){}; bool operator < (const Node & rhs) const{ return this->h < rhs.h; }; }s[maxn]; inline void pushup(int rt, int l, int r) { if(add[rt]) sum[rt] = x[r+1] - x[l];/// 这里每一个 l 和 r 是离散化后的值 /// 所以应当代入 x 数组来获取真实值 else if(l == r) sum[rt] = 0; else sum[rt] = sum[rt<<1] + sum[rt<<1|1]; } inline void update(int L, int R, int c, int l, int r, int rt) { int m; if(L <= l && r <= R){ add[rt] += c; pushup(rt, l, r); return ; } m = (l+r)>>1; if(L <= m) update(L, R, c, lson); if(R > m) update(L, R, c, rson); pushup(rt, l, r); } int main(void) { int n; scanf("%d", &n); int x1, x2, y1, y2; int num = 0; for(int i=0; i<n; i++){ scanf("%d %d %d %d", &x1, &y1, &x2, &y2); x1 += Base, x2 += Base, y1 += Base, y2 += Base;/// 因为有负数坐标的存在,所以需要加上一个基数 x[num] = x1;/// 记录所有出现的横坐标的值,方便离散化 s[num++] = Node(x1, x2, y1, 1); /// 将所有的横边(与x轴平行)以及其高度存储起来 x[num] = x2; s[num++] = Node(x1, x2, y2, -1);/// 顶边 flag == 1 而底边 flag == -1 是为了方便 /// 从上到下扫描的时候做到,计入及删除这个矩形操作 } sort(x, x+num); sort(s, s+num); int idx = std::unique(x, x+num) - x;/// 离散化横坐标 int L, R; long long ans = 0;/// Attention !!! for(int i=0; i<num-1; i++){ L = lower_bound(x, x+idx, s[i].l) - x;/// 找出线段树应当更新的左右界,注意是使用离散化后的值 R = lower_bound(x, x+idx, s[i].r) - x - 1; update(L,R,s[i].flag,0,idx-1,1);/// 根据 flag 来确定是要删除还是添加操作 ans+=(sum[1]*(1LL*s[i+1].h-1LL*s[i].h));/// 最后用当前存在的横坐标的总和去乘高度就是面积了,累加起来 } printf("%lld\\n", ans); return 0; }
类似题目 : HDU 1542 Atlantis

#include<bits/stdc++.h> #define LL long long #define lson l, m, rt<<1 #define rson m+1,r,rt<<1|1 using namespace std; const int maxn = 505; int add[maxn]; double x[maxn<<2], sum[maxn<<2]; struct Node{ int flag; double l, r, h; Node(){}; Node(double L, double R, double H, int F):l(L),r(R),h(H),flag(F){}; bool operator < (const Node & rhs) const{ return this->h < rhs.h; }; }s[maxn]; inline void pushup(int rt, int l, int r) { if(add[rt]) sum[rt] = x[r+1] - x[l]; else if(l == r) sum[rt] = 0; else sum[rt] = sum[rt<<1] + sum[rt<<1|1]; } inline void update(int L, int R, int c, int l, int r, int rt) { int m; if(L <= l && r <= R){ add[rt] += c; pushup(rt, l, r); return ; } m = (l+r)>>1; if(L <= m) update(L, R, c, lson); if(R > m) update(L, R, c, rson); pushup(rt, l, r); } int main(void) { int Case = 1, n; while(~scanf("%d", &n) && n){ double x1, x2, y1, y2; int num = 0; for(int i=0; i<n; i++){ scanf("%lf %lf %lf %lf", &x1, &y1, &x2, &y2); x[num] = x1; s[num++] = Node(x1, x2, y1, 1); x[num] = x2; s[num++] = Node(x1, x2, y2, -1); } sort(x, x+num); sort(s, s+num); int idx = std::unique(x, x+num) - x; memset(add, 0, sizeof(add)); memset(sum, 0, sizeof(sum)); int L, R; double ans = 0; for(int i=0; i<num-1; i++){ L = lower_bound(x, x+idx, s[i].l) - x; R = lower_bound(x, x+idx, s[i].r) - x - 1; update(L,R,s[i].flag,0,idx-1,1); ans+=(sum[1]*(s[i+1].h-s[i].h)); } printf("Test case #%d\\nTotal explored area: %.2lf\\n\\n", Case++, ans); } return 0; }
类似知识点 : 利用扫描线求矩形周长并
