cdq分治解决区间问题

Posted 2020-10-21 Nico&11101001

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3个整数，表示一个操作，具体如下：

操作1： 格式：1 x k 含义：将第x个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

 

输出格式：

 

输出包含若干行整数，即为所有操作2的结果。

 

输入输出样例

输入样例#1： 复制

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出样例#1： 复制

14
16

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

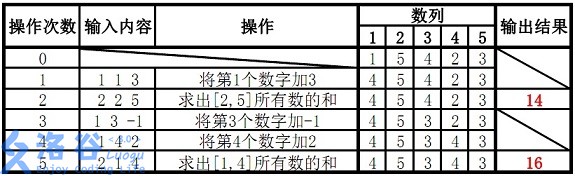
故输出结果14、16

#include<cstdio>
#include<algorithm>
const int maxn = 2220007;
inline int read() {
    int x=0,f=1;char c=getchar();
    while(c<‘0‘||c>‘9‘) {
        if(c==‘-‘)f=-1;c=getchar();
    }
    while(c<=‘9‘&&c>=‘0‘) {
        x=x*10+c-‘0‘,c=getchar();
    }
    return x*f;
}
int n,m,tot,t,ans[maxn];
struct node{
    int x,key,id,kind,bl;
    bool operator < (const node&a)const {
        if(x!=a.x) return x<a.x;
        else return kind<a.kind;
    }
}q[maxn],tmp[maxn];
void cdq(int l,int r) {
    if(l==r) return;
    int sum=0;
    int mid=l+r>>1,ll=l,rr=mid+1;
    for(int i=l;i<=r;i++) {
        if(q[i].kind==1&&q[i].id<=mid) sum+=q[i].key;
        else if(q[i].kind==2&&q[i].id>mid)  ans[q[i].bl]+=q[i].key*sum;
    }
    for(int i=l;i<=r;i++) {
        if(q[i].id<=mid)tmp[ll++]=q[i];
        else tmp[rr++]=q[i];
    }
    for(int i=l;i<=r;i++) q[i]=tmp[i];
    cdq(l,mid);cdq(mid+1,r);
}
int main()
{
    n=read(),m=read();
    for(int x,i=1;i<=n;i++) {
        x=read();
        q[++tot].x=i;q[tot].key=x;q[tot].id=tot;q[tot].kind=1;
    }
    for(int x,y,z;m;m--) {
        scanf("%d%d%d",&x,&y,&z);
        if(x&1) { 
            q[++tot].x=y;q[tot].key=z;q[tot].id=tot;q[tot].kind=1;
        }
        else {
            q[++tot].x=y-1;q[tot].key=-1;q[tot].id=tot;q[tot].kind=2;q[tot].bl=++t;
            q[++tot].x=z;q[tot].key=1;q[tot].id=tot;q[tot].kind=2;q[tot].bl=t;//id : kth operator ,x:the location of the op ;bl : the group of the query sum
        }
    }
    std::sort(q+1,q+tot+1);
    cdq(1,tot);
    for(int i=1;i<=t;i++) 
        printf("%d\n",ans[i]);
    return 0;
}