CDQ分治复习

Posted 2022-03-04 Harris-H

CDQ分治复习

1.二维区间翻转、二维区间求和

可以转化为三维偏序，第一维是按时间顺序，因为题意是按顺序给的，所以第一维解决，接下来第二维是x，第三维是y。

第二维采用归并排序很容易，第三维用BIT维护。

这里BIT我们维护差分数组。

区间求和

区间求和可以拆成4个前缀和的容斥。

然后前缀和可以用差分数组表示。

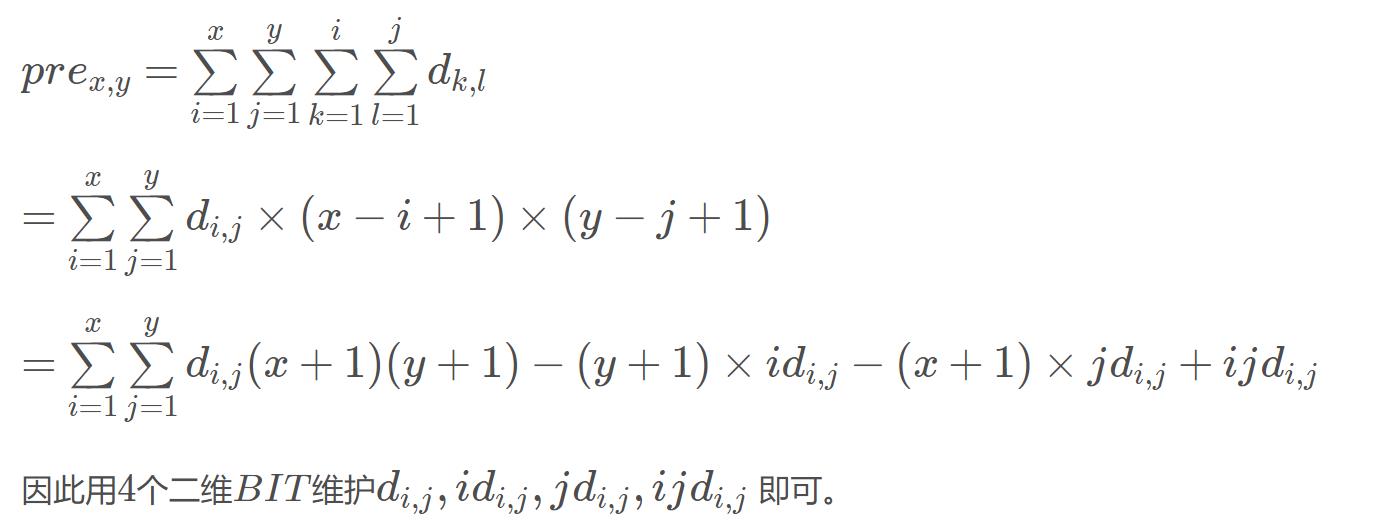
通过4个BIT我们就可以logn实现修改和查询了。

区间翻转

区间翻转其实等价于模2下的区间加法。

而区间加法可以用差分数组直接实现。

因为我们前面维护的4个BIT，所以这里的W也要乘上对应的参数(1，i，j，ij)

时间复杂度：$O(nlo{g}^{2}n)$

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull; 
const int N=1e5+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7;
const int hashmod[4] = 402653189,805306457,1610612741,998244353;
#define mst(a,b) memset(a,b,sizeof a)
#define db double
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define x first
#define y second
#define pb emplace_back
#define SZ(a) (int)a.size()
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define per(i,a,b) for(int i=a;i>=b;--i)
#define ios ios::sync_with_stdio(false),cin.tie(nullptr) 
void Print(int *a,int n)
	for(int i=1;i<n;i++)
		printf("%d ",a[i]);
	printf("%d\\n",a[n]); 

template <typename T>		//x=max(x,y)  x=min(x,y)
void cmx(T &x,T y)
	if(x<y) x=y;

template <typename T>
void cmn(T &x,T y)
	if(x>y) x=y;

struct node
	int x,y,f,id;
a[N<<2],a2[N<<2];
int n,q,nq,Q;
int ans[N];
struct BIT
	#define lowbit(x) x&(-x)
	#define il inline
	ll s[N];
	il void add(int x,int v)
		while(x<=1e5)
			s[x]+=v;x+=lowbit(x);
		return;
	
	il ll que(int x)
		ll ans=0;
		while(x)
			ans^=s[x];x-=lowbit(x);
		return ans;
	
A,Ai,Aj,Aij;
void cdq(int l,int r)
	//printf("(%d,%d)\\n",l,r);
	if(l==r) return;
	int m=l+r>>1;
	cdq(l,m),cdq(m+1,r);
	int L=l,R=m+1;
	for(;R<=r;R++)
		if(a[R].id)
			for(;L<=m&&a[L].x<=a[R].x;L++) 
			if(!a[L].id)
				A.add(a[L].y,a[L].f);
				Ai.add(a[L].y,a[L].x*a[L].f);
				Aj.add(a[L].y,a[L].y*a[L].f);
				Aij.add(a[L].y,1LL*a[L].x*a[L].y*a[L].f);
			
			int x = a[R].x,y=a[R].y;
			ans[a[R].id]+=(1LL*A.que(y)*(1LL*x*y+x+y+1)*a[R].f)%2;
			ans[a[R].id]+=(1LL*Ai.que(y)*(y+1)*a[R].f)%2;
			ans[a[R].id]+=(1LL*Aj.que(y)*(x+1)*a[R].f)%2;
			ans[a[R].id]+=(1LL*Aij.que(y)*a[R].f)%2;
		
	for(int i=l;i<L;i++) if(!a[i].id)
				A.add(a[i].y,-a[i].f);
				Ai.add(a[i].y,-a[i].x*a[i].f);
				Aj.add(a[i].y,-a[i].y*a[i].f);
				Aij.add(a[i].y,-1LL*a[i].x*a[i].y*a[i].f);
	
	L=l,R=m+1;
	for(int i=l;i<=r;i++)
		if(R>r||(L<=m&&a[L].x<=a[R].x)) a2[i]=a[L++];
		else a2[i]=a[R++];
	for(int i=l;i<=r;i++) a[i]=a2[i];

int main()
	scanf("%d%d",&n,&q);
	rep(i,1,q)
		int op,x1,y1,x2,y2;
		scanf("%d%d%d%d%d",&op,&x1,&y1,&x2,&y2);
		
		if(op==1)
			a[++nq]=x1,y1,1,0;
			a[++nq]=x2+1,y1,-1,0;
			a[++nq]=x1,y2+1,-1,0;
			a[++nq]=x2+1,y2+1,1,0;
		else if(op==2)
			++Q;
			a[++nq]=x2,y2,1,Q;
			a[++nq]=x2,y1-1,-1,Q;
			a[++nq]=x1-1,y2,-1,Q;
			a[++nq]=x1-1,y1-1,1,Q;			
		
	
	cdq(1,nq);
	rep(i,1,Q) printf("%d\\n",ans[i]&1);
	return 0;

---

总结

cdq分治是解决多维偏序的算法。

许多区间统计问题可以通过容斥转化为偏序问题(也就是多维前缀和)，这也是为什么最后一维通常可以用BIT进行维护的原因。