Motivation 问题描述
收集到某一地区的房子面积和房价的数据(x, y)42组,对于一套已知面积的房子预测其房价?
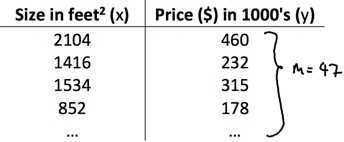 ?
?
 ?
?
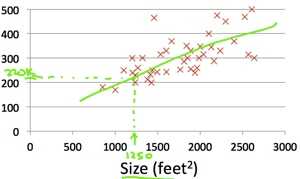
由房价数据可视化图可以看出,可以使用一条直线拟合房价。通过这种假设得到的预测值和真实值比较接近。
Model 模型
将现实的问题通过数学模型描述出来。
m 个 样本(example)组成训练集(training set),每一个样本有n个特征(feature)和一个标签(label)。目的是,通过一个数学模型(algorithm)和参数(parameters)将每一个样本和标签映射。这样,给定一个未知的样本就可以通过建立的数学模型预测其标签。
| 参数 | 解释 |
|---|---|
| m | 样例数 training set |
| n | 特征数 no. of features |
| X | (m*(n+1)) |
| y | (m*1) |
| \\(\\Theta\\) | ((n+1)*1) \\(X\\theta=y\\) |
Hypothesis 假设
假设房价由此方程拟合
\\[h_\\theta(x) = \\theta_0+\\theta_1x\\]
其中\\(\\theta_0\\)为偏置bias,\\(\\theta_1\\)为因变量的权重weight
Cost function 损失函数
需要一个函数评价拟合函数的预测效果如何。直观的,我们可以计算真实房价和预测房价的差值平方和J,J越小预测效果越好。所以,可以通过最小化J可以求出参数\\(\\theta_0\\)和\\(\\theta_1\\)的值。
\\[J(\\theta_0,\\theta_1)=\\frac 1 {2m}\\sum_{i=1}^m(h_\\theta(x^{(i)})-y^{(i)})^2\\]
Gradient descent 梯度下降
这是一个二元函数求极值的问题。可以使用求偏导的方法找出所有极值点,然后代入损失函数求出最小值。一般的做法是采用梯度下降法。梯度下降选择一个系数alpha,和迭代次数。
repeat until convergence {
\\[\\theta_0 := \\theta_0 - \\alpha\\frac 1 {2m}\\sum_{i=1}^m(h_\\theta(x^{(i)})-y^{(i)})\\]
\\[\\theta_1 := \\theta_1 - \\alpha\\frac 1 {2m}\\sum_{i=1}^m(h_\\theta(x^{(i)})-y^{(i)})\\cdot{x^{(i)}}\\]
}
下图是二维梯度下降可视化
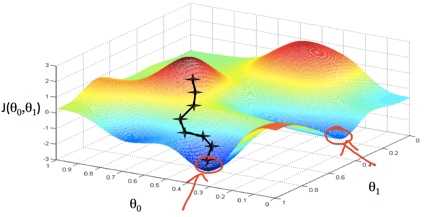 ?
?
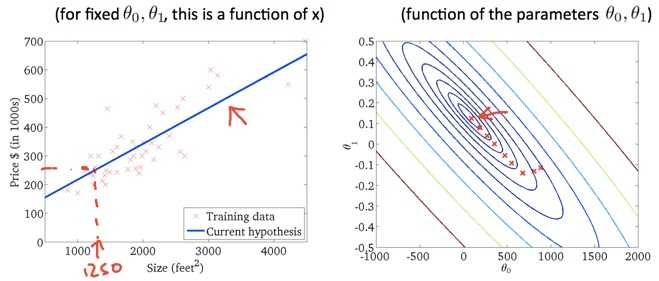 ?
?
通过这种方式可以得出假设的参数。对于已知房子面积的房子就可以使用假设估计房价了。值得一提的是预测的房价不可能是100%准确,但是可以认为是在给定条件下最接近真实房价的值。
注意,梯度下降求的的只是极值点,有可能陷入局部最优,但是对于凸函数,极值点就是最值点,因为极值点只有一个。
LG with multiple variables 多元线性回归
更一般的情况是房价可能由多种因素综合决定,像房子年龄,卧室数目和楼层数。
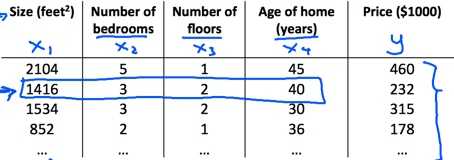 ?
?
这时hypothesis变为
\\[h_\\theta = \\theta_0 + \\theta_1x_1 + \\cdots + \\theta_nx_n\\]
cost function变为
\\[J(\\theta_0,\\theta_1, \\cdots ,\\theta_n)=\\frac 1 {2m}\\sum_{i=1}^m(h_\\theta(x^{(i)})-y^{(i)})^2\\] gradient descent变为
\\[\\theta_j := \\theta_j - \\alpha\\frac 1 {2m}\\sum_{i=1}^m(h_\\theta(x^{(i)})-y^{(i)})\\cdot{x^{(i)}_j}\\]
注意使用feature scaling将不同范围的特征映射到相近的范围。
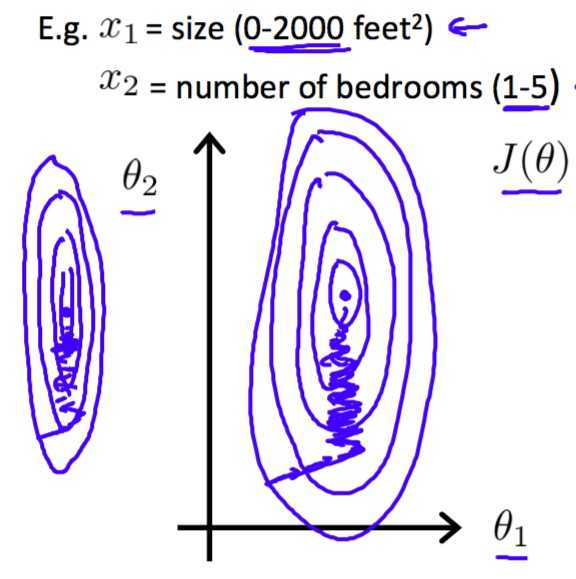 ?
?
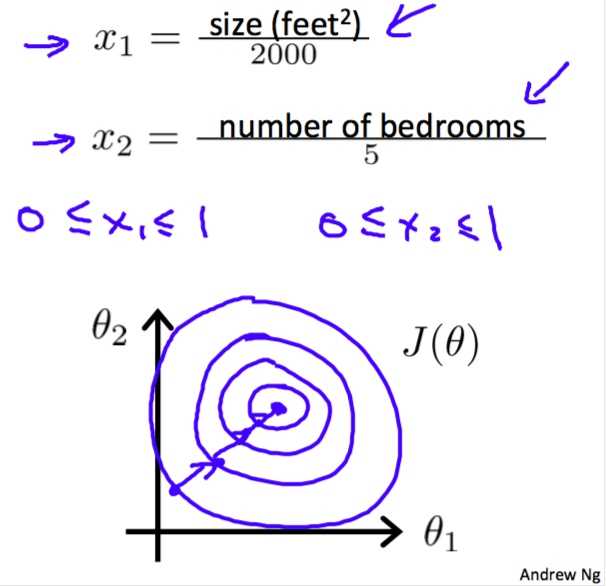 ?
?
Polynomial regression多项式回归
更一般的情况是房价和面积是如下图的关系。解决方法转化为多元线性回归。
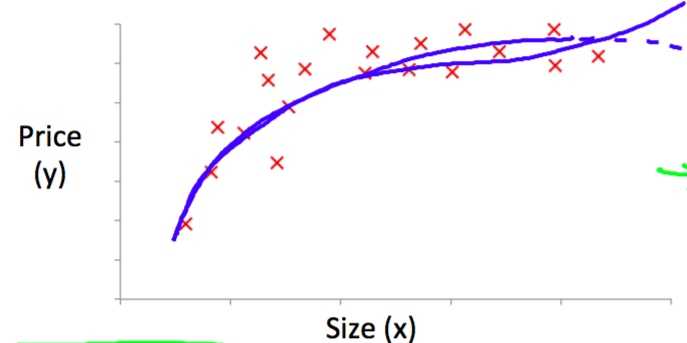 ?
?
在这种情况下,一种可能是选择以下特征
\\[x_1=size,x_2=(size)^2\\]
hypothesis 为
\\[h_\\theta(x)=\\theta_0+\\theta_1(size)+\\theta_2(size)^2\\]
即为
\\[h_\\theta(x)=\\theta_0+\\theta_1x_1+\\theta_2x_2\\]
通过这种方法就可以转换为多元线性回归问题。
Normal Equation
使用多元函数求极值的方法。只是以向量的方式表示。
当除了使用梯度下降外,还可以使用normal equation求参数。
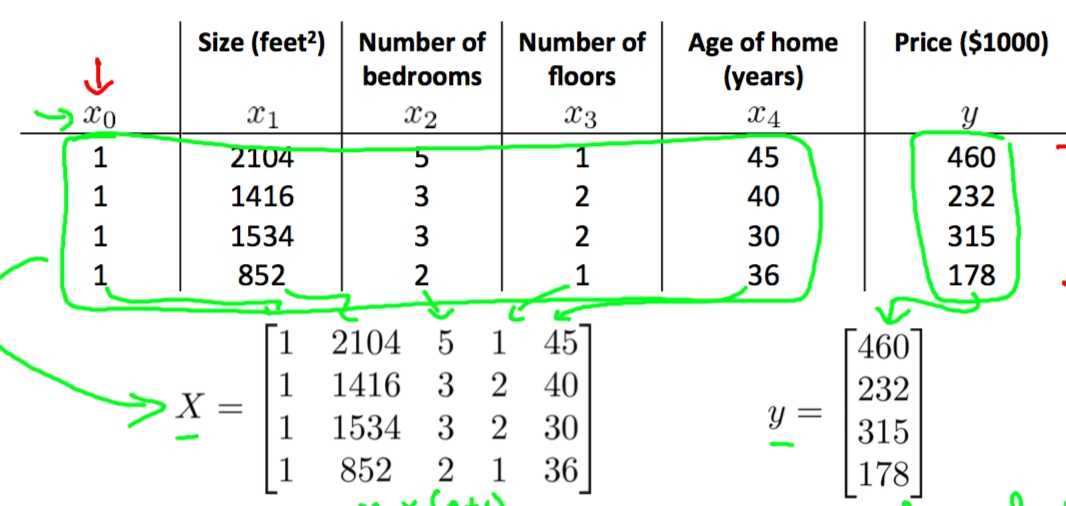 ?
?
\\[X\\theta=y\\]
解得
\\[\\theta=(X^TX)^{-1}X^Ty\\]
注意当features数多于样本数的情况
解决办法增加样本数,减少特征数,使用normalization
References