GMM,即高斯混合模型(Gaussian Mixture Model),简单地讲,就是将多个高斯模型混合起来,作为一个新的模型,这样就可以综合运用多模型的表达能力。EM,指的是均值最大化算法(expectation-maximization),它是一种估计模型参数的策略,在 GMM 这类算法中应用广泛,因此,有时候人们又喜欢把 GMM 这类可以用 EM 算法求解的模型称为 EM 算法家族。
这篇文章会简单提一下 GMM 模型的内容,最主要的,还是讲一下 EM 算法如何应用到 GMM 模型的参数估计上。
高斯混合模型
什么是 GMM
GMM 可以认为是 K-means 算法的升级版。在 K-means 中,我们会先计算出几个聚类中心,然后根据数据点与聚类中心的距离,直接将数据点归类到最近的聚类中心。这种做法其实很“硬”,因为有很多边缘点属于两个聚类中心的概率可能相差不大,如果一股脑就直接将它归到某一个中心,实在是太粗暴了。而 GMM 不同于 K-means 的地方就在于,它除了给出聚类中心外,还能告诉你每个点归属于某个聚类中心的概率,因此,GMM 又被称作 soft assignment。
首先,还是给出 GMM 模型的公式:
其中,我们规定,\\(\\sum_{k=1}^K{\\pi_k}=1\\)。可以看出,GMM 就是将几个高斯模型线性组合起来,人们习惯上把这里面的各个高斯模型称为 Component。其中,\\(\\pi_k\\) 表示每个模型的占比,或者说数据属于模型 k 的概率,这个值越大,说明聚集在这个模型内的数据越多。
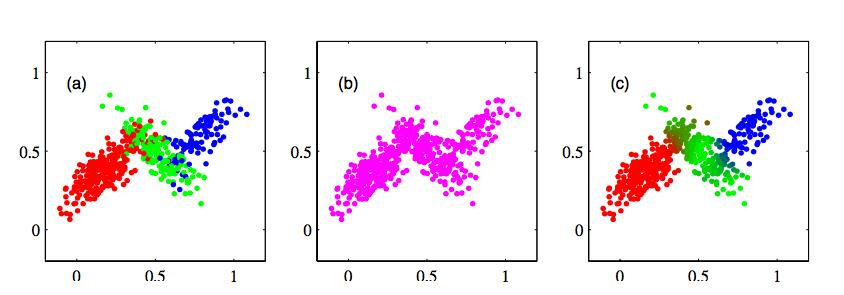
为什么要用这种模型组合的方式呢?我们知道,高斯模型一般成椭圆状(二维)或椭球状(三维),可以把这个椭圆或椭球认为是一种聚类的形状,而圆心或球心则是聚类中心(对应高斯函数的参数 \\(\\mu\\))。但真实世界中,数据的分布并不一定都是按这样的形状分布的(如上面给出的图),因此,一个高斯模型可能没法很好的拟合这些数据,而如果能综合考虑几个高斯模型的表达能力,让这些模型发挥所长,不同的模型拟合不同的数据,这样一来,所有数据就可以很好地被这个「组合模型」拟合起来。
其实,这种组合模型的思路可以应用到很多模型上,比如:泊松模型。而由于高斯模型本身一些良好的性质,因此 GMM 这种模型被用的比较多。
前面说到,GMM 本质上是一种聚类算法,那么,如果已知一个 GMM 模型,现在给定一个点,我们要怎么知道这个点属于哪个聚类中心呢?更具体一点说,怎么知道这个点属于每个聚类中心的概率是多少?
用数学的语言表达就是,已知一个 GMM 模型: \\(p( x)=\\sum_{k=1}^K{\\pi_k N( x|\\mu_k, \\Sigma_k)}\\),它的 K 个聚类中心为 \\(C_k\\),现在要求概率值 \\(p( x \\in C_k | x)\\)。
求解的方法很简单,根据贝叶斯公式:\\(p(a|b)=\\frac{p(b|a)p(a)}{p(b)}\\),我们可以得出:
因此,对于每个聚类中心 \\(C_k\\),由于分母 \\(p( x)\\) 都是相同的,我们只需要计算 \\(p(C_k)p( x| x\\in C_k)=\\pi_k N( x|\\mu_k, \\Sigma_k)\\) 即可。得到的值就是数据点 $ x$ 属于 \\(C_k\\) 的概率,至于具体要将 $ x$ 归类到哪个中心,可以根据具体情况决定,比如将概率最大的作为归属的聚类中心。这一点也是 GMM 优于 K-means 的地方,前者是通过概率的方式来决定归属,因此提供了更加丰富的信息。
参数估计
不过,GMM 模型最难的地方在于,如何根据一堆数据点估计出模型的参数?
GMM 需要确定的参数有三类:
- 高斯模型的个数 \\(K\\),这个参数跟 K-means 的 \\(K\\) 一样,需要人工事先设定,\\(K\\) 越大,聚类的粒度也越细;
- \\(\\pi_k\\), 每个 Component 的概率分量,或者说在总样本中的占比;
- \\(\\mu_k\\)、\\(\\Sigma_k\\),各个 Component 的参数。
如果样本所属分类已知(即已知 \\(x\\) 属于哪个 \\(C_k\\)),那 GMM 的参数就很容易确定了。首先,参数 \\(K\\) 就一目了然得到了。然后,假设样本容量为 \\(N\\),归属于聚类中心 \\(C_k\\) 的样本数量为 \\(N_k\\),归属每个 \\(C_k\\) 的样本集合为 \\(S(k)\\),可以用以下公式求出其他参数:
其实,这跟一个高斯模型的情况是一样的,只不过要依葫芦画瓢求出 \\(K\\) 个。
但如果样本的分类事先不知道,又该怎么办呢?首先,由于 \\(K\\) 这个值是需要人工确定的,所以这里暂时假设 \\(K\\) 已经知道了。现在,我们要预测 \\(K\\) 个高斯模型的概率分量 \\(\\pi_k\\) 以及每个模型各自的参数 \\(\\mu_k\\) 和 \\(\\Sigma_k\\)。
最简单也最容易想到的方法是极大似然估计。假设有 m 个样本,首先,写出 \\(p( x)=\\sum_{k=1}^K{\\pi_k N( x|\\mu_k, \\Sigma_k)}\\) 的似然函数:
不过,这个对数函数却出奇的复杂,直接求导数的方法很难求出 \\(\\mu_k\\) 和 \\(\\Sigma_k\\),因此,我们只能换用其他方式来求解。而这就是 EM 算法发挥作用的地方。
均值最大化算法 EM
K-means 的启示
在正式开讲 EM 之前,我们先回忆一下,K-means 是怎么求出聚类中心的。其实,总共分三步进行:
- 随机初始化 K 个聚类中心的位置;
- 将所有样本点,按照跟各个聚类中心的距离进行归类;
- 根据样本重新归类的结果,更新聚类中心的位置,重复步骤 2 直到收敛(即聚类中心重新调整的幅度小于某个阈值)。
既然 GMM 本身也属于一种聚类算法,那么,我们能不能用 K-means 的思路来求出 GMM 的参数呢?答案当然是可以的。
不过,在这之前,我们需要先知道 GMM 的几个参数(\\(\\pi_k\\),\\(\\mu_k\\),\\(\\Sigma_k\\))要怎么计算。假设我们已经知道了后验概率 \\(P( x \\in C_k| x)\\),则可以根据以下公式计算参数(其中,m 表示样本数量):
这个公式是把所有样本属于 \\(C_k\\) 的概率求平均后,作为 \\(C_k\\) 这个聚类中心(或者说这个高斯模型)的出现概率。
这个求均值的公式,跟单个高斯模型不同的地方在于,我们用的是加权平均。因为每个样本点都有一定的概率属于聚类中心 \\(C_k\\),所以,每个样本对 \\(C_k\\) 对应的高斯模型的均值也会产生一定的作用,只是由于 \\(P(x_i\\in C_k|x_i)\\) 的值不同,因此这种作用也会有显著差别。
类似地,协方差也是用加权平均求出来的。
(公式 (3) (4) (5) 其实是从极大似然函数推出来的,在周志华老师的西瓜书和PRML书中都有详细推导,不过这里我只想给出感性的认识)
不过,以上公式都是基于 \\(P( x \\in C_k| x)=\\frac{p(C_k)p( x| x\\in C_k)}{p( x)}\\)计算出来的,而这个公式本身又需要知道 \\(P(C_k)\\)(即 \\(\\pi_k\\))等参数,这就陷入一个鸡生蛋还是蛋生鸡的怪圈。
但是,借助 K-means 的思路,我们可以事先随机初始化这些参数,然后计算出 \\(P( x \\in C_k| x)\\),再用它更新 GMM 参数,然后再用更新的模型计算 \\(P( x \\in C_k| x)\\),如此迭代下去,总有收敛的时候,这样,我们不就可以像 K-means 一样计算出参数了吗?!
下面,我们就仿照 K-means 的方法,给出迭代计算 GMM 参数的步骤:
- 随机初始化各个高斯模型的参数;
- 根据参数,计算 \\(P( x \\in C_k| x)\\),这一步其实是计算出每一个样本归属于每一个聚类中心的概率;
- 根据第 2 步计算得到的 \\(P( x \\in C_k| x)\\),按照公式 (3) (4) (5) 重新计算 GMM 参数,并重复步骤 2 直到收敛。
EM 算法
其实,上面仿照 K-means 算法的计算步骤,就是 EM 算法的核心部分了。
EM 算法主要分为 E 和 M 两步:
- E 指的是 Expectation,即计算均值的过程,对应的是上面的步骤 2,这一步主要是计算每个样本归属的聚类中心;
- M 指的是 Maximum,即对参数的最大似然估计,对应的是上面的步骤 3。我前面也说了,公式 (3) (4) (5) 计算参数的公式是用最大似然函数推出来的,所以,这一步其实是在根据步骤 2 的分类结果,重新用最大似然函数来估计参数。
下面这幅图是从西瓜书上截下来的,是 EM 算法求解 GMM 参数的完整过程。

图中有很多公式标记,可能要参考原书才看得懂,不过,它的流程和我之前给出的 3 个步骤是一致。另外,算法的停止条件可以是达到最大迭代次数,或者是似然函数(公式 (2))的增长小于某个阈值。
好了,本文到这里就不再深入下去了。EM 算法博大精深,吴军老师在《数学之美》称它为上帝的算法,可见这个算法的强大之处。EM 算法可以应用的场合非常多,从本文给出的 GMM 例子来看,它其实很类似梯度下降算法,在给定的目标函数很复杂、难以求解时,EM 算法用一种迭代的策略来优化初始参数,并逐步收敛到最优解。关于这个算法的具体内容,我想进一步深入理解后,再用一篇文章好好写一下。