20210916GMM入门
Posted Yang SiCheng
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了20210916GMM入门相关的知识，希望对你有一定的参考价值。
高斯混合模型GMM（Gaussian Mixture Model）
1. 模型介绍
高斯——高斯分布
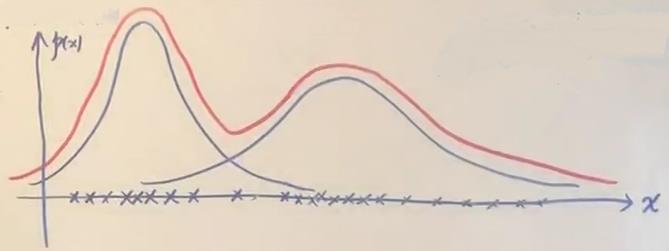
从概率密度估计的角度来看 ，从几何角度来看，加权（
α
\\alpha
α）平均→多个高斯分布叠加而成
p
(
x
)
=
∑
k
=
1
k
α
k
N
(
μ
k
,
Σ
k
)
,
∑
k
=
1
k
α
k
=
1
(1)
p(x)=\\sum_{k=1}^{k} \\alpha_{k} N\\left(\\mu_{k}, \\Sigma_{k}\\right), \\sum_{k=1}^{k} \\alpha_{k}=1\\tag{1}
p(x)=k=1∑kαkN(μk,Σk),k=1∑kαk=1(1)
∑
α
k
=
1
\\sum \\alpha_{k}=1
∑αk=1
上式中
α
k
\\alpha_k
αk为权重
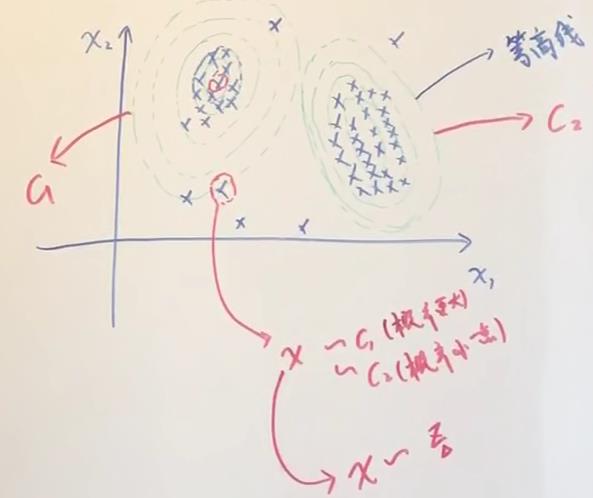
从混合（生成）模型的角度来看（生成模型）
x：observed variable
z：latent variable
z表示对应的样本x是属于哪一个高斯分布，这是一个离散的随机变量
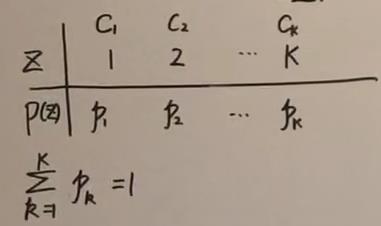
生成过程，概率图（有向图）如下：（观测图用阴影表示）
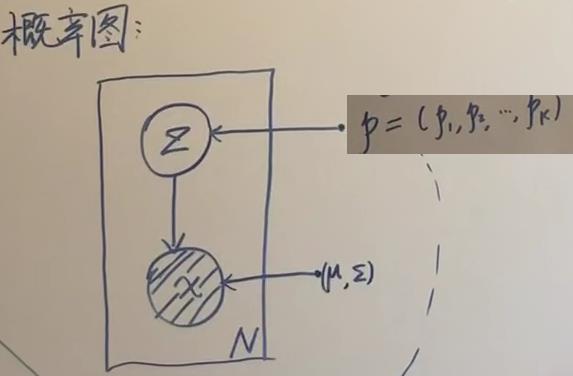
联合概率密度可转化为乘法的形式：
p
(
x
)
=
∑
z
p
(
x
,
z
)
=
∑
k
=
1
k
p
(
x
,
z
=
c
k
)
=
∑
k
=
1
k
p
(
z
=
c
k
)
⋅
p
(
x
∣
z
=
c
k
)
=
∑
k
=
1
K
p
k
⋅
N
(
x
∣
μ
k
Σ
k
)
(2)
\\begin{aligned} p(x) &=\\sum_{z} p(x, z) \\\\ &=\\sum_{k=1}^{k} p\\left(x, z=c_{k}\\right) \\\\ &=\\sum_{k=1}^{k} p\\left(z=c_{k}\\right) \\cdot p\\left(x \\mid z=c_{k}\\right) \\\\ &=\\sum_{k=1}^{K} p_{k} \\cdot N\\left(x \\mid \\mu_{k} \\Sigma_{k}\\right) \\end{aligned}\\tag{2}
p(x)=z∑p(x,z)=k=1∑kp(x,z=ck)=k=1∑kp(z=ck)⋅p(x∣z=ck)=k=1∑Kpk⋅N(x∣μkΣk)(2)
上式中
p
k
p_k
pk为概率值，可见与式(1)相同
2. 极大似然估计MLE（Maximum Likelihood Estimate）
X：observed data （
X
=
(
x
1
,
x
2
,
.
.
.
,
x
N
)
X=(x_1,x_2,...,x_N)
X=(x1,x2,...,xN)）
(X,Z)：complete data
θ
\\theta
θ：parameter （
θ
\\theta
θ={
p
1
,
p
2
,
.
.
.
,
p
k
,
μ
1
,
μ
2
,
.
.
.
,
μ
k
,
Σ
1
,
Σ
2
,
.
.
.
,
Σ
k
p_1,p_2,...,p_k,\\mu_1,\\mu_2,...,\\mu_k,\\Sigma_1,\\Sigma_2,...,\\Sigma_k
p1,p2,...,pk,μ1,μ2,...,μk,Σ1,Σ2,...,Σk}）
θ
^
M
L
E
=
arg
max
θ
log
P
(
x
)
\\hat{\\theta}_{MLE}=\\arg \\max _{\\theta} \\log P(x)
θ^MLE=argθmaxlogP(x)
样本之间相互独立，上式可写为相乘的形式
θ
^
M
L
E
=
arg
max
θ
log
∏
i
=
1
N
P
(
x
i
)
=
arg
max
∑
i
=
1
N
log
P
(
x
i
)
\\hat{\\theta}_{MLE}=\\arg \\max _{\\theta} \\log \\prod_{i=1}^{N} P\\left(x_{i}\\right)=\\arg \\max \\sum_{i=1}^{N} \\log P\\left(x_{i}\\right)
θ^MLE=argθmaxlogi=1∏NP(xi)=argmaxi=1∑NlogP(xi)
将式(2)代入，得
θ
^
M
L
E
=
arg
max
θ
∑
i
=
1
N
log
∑
k
=
1
k
p
k
⋅
N
(
x
i
∣
μ
k
,
Σ
k
)
\\hat{\\theta}_{MLE}=\\arg \\max _{\\theta} \\sum_{i=1}^{N} \\log \\sum_{k=1}^{k} p_{k} \\cdot N\\left(x_{i} \\mid \\mu_{k}, \\Sigma_{k}\\right)
θ^MLE=argθmaxi=1∑做和准备做的一些杂七杂八的题(20210916start)