稀疏傅里叶变换（sparse FFT）

Posted 2020-10-19 桂。

作者：桂。

时间：2018-01-06  14:00:25

链接：http://www.cnblogs.com/xingshansi/p/8214122.html 

---

前言

　　对于数字接收来讲，射频域随着带宽的增加，AD、微波、FPGA资源的需求越来越高，但频域开的越宽并不意味着频谱越宽，有限信号内可认为信号在宽开频域稀疏分布，最近较为流行的稀疏FFT（SFFT）是在传统FFT的基础上，利用了信号的稀疏特性，使得计算性能优于FFT。本文简单记录自己的理解。

源代码

一、稀疏FFT

主要是12年MIT的论文：Simple and Practical Algorithm for Sparse Fourier Transform。

核心思想：

SFT 作为这样一种“输出感知”算法,其核心思路是按照一定规则 Γ ( • )将信号频点投入到一组“筐”中(数量为 B，通过滤波器实现 ) . 因频域是稀疏的,各大值点将依很高的概率在各自的“筐”中孤立存在 . 将各“筐”中频点叠加,使 N 点长序列转换为 B点的短序列并作 FFT 运算,根据计算结果,忽略所有不含大值点的“筐”,最后根据对应分“筐”规则,设计重构算法 Γ ^-1 ( • )恢复出 N 点原始信号频谱。

算法流程：

步骤一：选定一个sigma，实现数据频域重排。

频域重排主要是因为FFT之后，频域大值集中在一起，需要将这一伙打散，保证频域的稀疏性（sparse）。打散之后就能稀疏，依据定理（可见n越大，打散的可能性越大，从这里看，sigma与B还是有关系的，sigma体现了相邻频点的最小间隔，而B决定了每个bucket的宽度）：

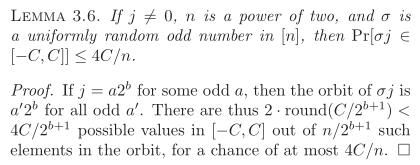
这里是按一定概率（概率性）将频谱重排，MIT重排思路：

对应代码：

fs = 1000;
f0 = 70;
N = 256;
t = [0:N-1]/fs;
x = exp(1j*2*pi*t*f0) ;
%%*************Step1:频谱随机重排**************
sigma = 19; %inv(sigma) = 27
tao = 3;
%permutation
perm_num = mod([1:N]*sigma+tao,N)+1;
pn = x(perm_num);

　　当然也有强制（确定性）将数据重排的思路，思路类似，只是实现方式不同：

sigma的选择主要利用性质：

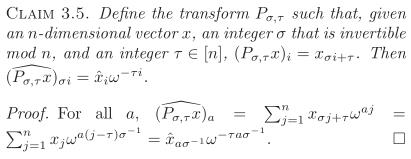
这里sigma^-1是sigma关于模N的逆元(数论倒数)。该点主要说明：变化前后的完备性（信号可重建）。

 步骤二：加窗。

 这里根据筐的多少（B），平分2pi频域，即带宽2pi/B，理想窗函数为矩形窗，但时域为无限长的sinc函数，需要加窗截断，可选择gausswin。

即win = sinc.*gausswin：

这里不局限于gausswin，满足给定约束的窗函数均可：

步骤三：频域抽取并作FFT

加窗之后，保证了频谱不至于展宽严重，进一步保证了稀疏性。频域降采样：

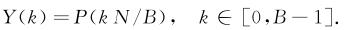
等价于时域的混叠的傅里叶变换：

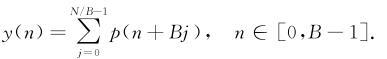
故直接在时域进行处理。处理完成后进行FFT运算。

该操作的理论基础为：

不谈加窗操作，x->p->y，可以看出x与y存在映射关系，而y的∑操作可以转化为并行，这样一来可以用多个低速率AD实现一个高速率AD的功能，前提是多个AD需要完全同步。

与上述降速率思想等价的是：如果各AD可做好同步，则多个现有AD的能力，可以做出现有AD难以完成的事。

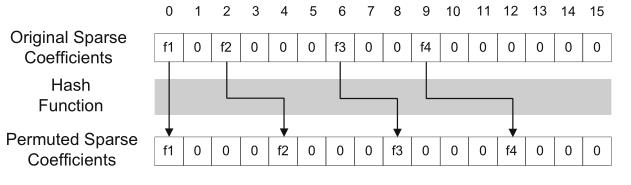
步骤四：哈希映射

哈希映射的线索为：最终观察的数据Y(k)【即y(n)】->P(k)【即p(n)】->X(k)【即x(n)】：

第一步（y -> p）转化的理论依据：

第二步（p -> x）转化的理论依据：

序列重排后的频域变换为：

这两步解释了算法step4的参数定义：

但实际中并非第一步提到的理想情况，实际情况是：

因此存在一个频谱重建的成功概率问题：

 4章节的后半部分主要在证明这个概率问题。

步骤五~六的主要目的，引用原文的说法：

　　Here are two versions of the inner loop: location loops and estimation loops. Location loops are given a parameter d, and output a set I ⊂ [n] of dkn/B  coordinates that contains each large coefficient with“good” probability. Estimation loops are given a set  I ⊂ [n] and estimate x I such that each coordinate is  estimated well with “good” probability.

 步骤五：定位循环

 d是一个参数，存在约束

原文取值为：

 该步骤的主要操作为：

将 Z ( k )中 dK 个较大值（从大到小依次排列）的坐标（ k）归入集合 J 中,通过哈希反映射得到 J 的原像：

这样便得到包含原始频谱坐标的集合，迭代L次：

迭代的目的？

 

步骤六：估值循环

 对于每个k∈Ir，计算频率信息：

步骤5~6主要操作：

至此完成了稀疏FFT（sparse FFT）的整个运算过程，记作sfft_v01。

改进版都是依次大框架进行，不同点主要有三个方面：1）重排的实现思路；2）频谱的重建思路。不再一一展开。 

原文示例：

该示例给出了步骤5~6的直观解释：

 

二、问题记录

仿真验证：n = 256点频信号，sigma = 19，则inv_sigma = 27，假设生成点频信号：

图1为重排的信号，图2为重排加窗(此处窗不够理想，看到长尾，论文中强调加窗，作用在于把尾巴剁掉。)，图3为原始信号频谱，图4为降采样之后的频谱。可以看出重排容易引入谐波：以sigma为周期。 　

原始频谱位置为k=10-1 = 9（下标从0开始），重排后对应频谱位置为mod(sigma*k,n) = 171 = 172-1，与理论分析一致。即原始k点重排后位置：

 即时域信号，x(n)，重排序号perm_num = mod([1:n]*sigma,n)+1，则对应重排后的傅里叶变换，频谱顺序与原信号频谱X，经过重排序号perm_num1 =  mod([1:n]*inv_sigma,n)+1，位置始终相差1（数论倒数的性质决定）:mod(sigma*inv_sigma,n)=1