FFT（快速傅里叶变换）

Posted 2023-05-10 2020fengziyang

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了FFT（快速傅里叶变换）相关的知识，希望对你有一定的参考价值。

FFT（快速傅里叶变换）

FFT（快速傅里叶变换）

前言

又要补之前的知识，艹。

快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

也就是说 ：FFT用来加速两个多项式的乘法。

建议学习一下有关复数的知识，这里 ~~我水了一篇博客。~~

多项式的系数表示法和点值表示法

系数表示法

一个\$n - 1\$ 次的 \$n\$ 项多项式 \$f(x)\$ 可以表示为 \$f(x) = \\sum_i= 0^n- 1 a_ix^i\$

即：

\\[f(x) = a_0 + a_1x^1 + a_2x^2+a_3x^3+\\cdots+a_n - 1x^n - 1 \\]

这就是我们平常最常用的 系数表示法

点值表示法

现在有一个多项式 \$f(x)\$ 我们可以把它在坐标系上表示出来

把多项式放到平面直角坐标系里面，看成一个函数
把 \$n\$ 个不同的 \$x\$ 代入，会得出 \$x\$ 个不同的 \$y\$，在坐标系内就是 \$n\$ 个不同的点
那么这 \$n\$ 个点 唯一确定 该多项式，也就是 有且仅有 一个多项式满足 $∀k, f(x_k) = y_k $ （这个其实跟插值差不多，大家可以看看这个拉格朗日插值法）

所以 \$f(x)\$ 就可以表示成 \$f(x) = (x_0 , f(x_0)),(x_1 , f(x_1))(x_2 , f(x_2) \\cdots (x_n - 1 , f(x_n - 1)))\$

这就是 点值表示法

高精度乘法下两种多项式表示法的区别

对于两个用系数表示的多项式，我们把它们相乘时。

很明显这个时间复杂度是 \$O(n)\$ 的

但是点值表示法就不太一样了，只需要 \$O(n)\$ 的时间。

假设两个点值多项式分别为

\\[f(x) = (x_0 , f(x_0)),(x_1 , f(x_1))(x_2 , f(x_2) \\cdots (x_n - 1 , f(x_n - 1))) \\newline g(x) = (x_0 , g(x_0)),(x_1 , g(x_1))(x_2 , g(x_2) \\cdots (x_n - 1 , g(x_n - 1))) \\]

设他们的乘积是 \$h(x)\$ 则

\\[h(x) = (x_0 , f(x_0)\\cdot g(x_0)),(x_1 , f(x_1)\\cdot g(x_1)),(x_2 , f(x_2)\\cdot g(x_2)), \\cdots (x_n - 1 , f(x_n - 1)\\cdot g(x_n - 1)) \\]

所以就只用枚举 \$O(n)\$ 就够了

好像我们只用把系数表示法转换成点值表示法就可以 \$O(n)\$ 解决多项式乘法了

朴素系数转点值的算法叫DFT（离散傅里叶变换），点值转系数叫IDFT（离散傅里叶逆变换）

但是我们朴素的系数转点值要 \$O(n^2)\$ ，所以我们要引入FFT

DFT

建议学习一下有关复数的知识，这里 ~~我水了一篇博客。~~

对于任意系数多项式转点值，当然可以随便取任意 \$n\$ 个 \$x\$ 值代入计算

但是这要 \$O(n^2)\$ 的时间。

傅里叶 提醒我们，

考虑一下，如果我们代入一些 \$x\$，使每个 \$x\$ 的若干次方等于 \$1\$ ，我们就不用做全部的次方运算了
$± 1 $是可以的，考虑虚数的话 \$± i\$ 也可以，但只有这四个数远远不够

他又说，这个圆上的所有数都可以

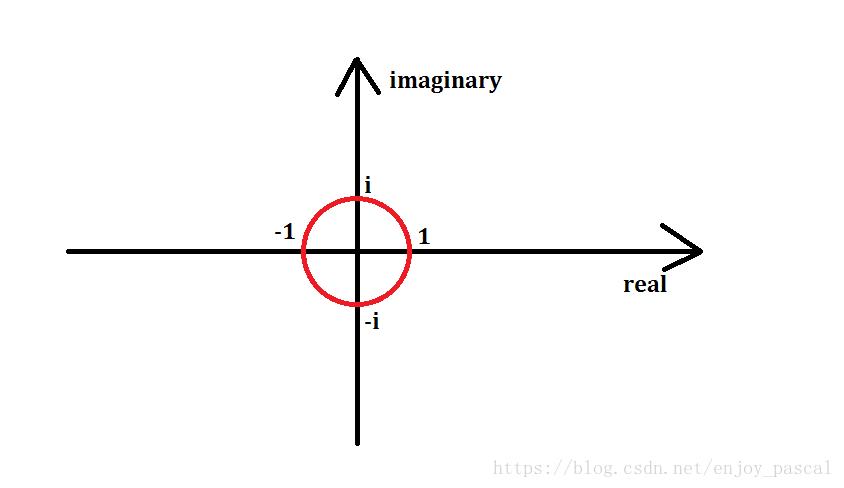
以原点为圆心，画一个半径为 \$1\$ 的单位圆

然后把它 \$n\$ 等分，如图是 \$n = 8\$

或者说：

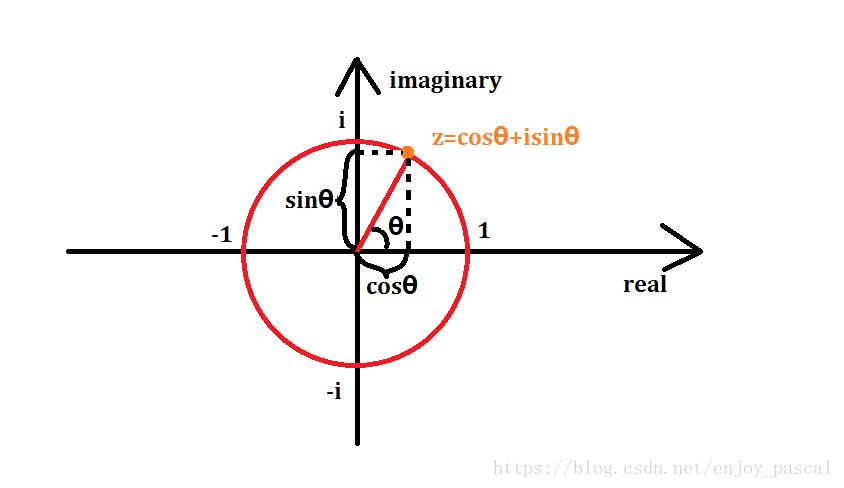
图上 \$w^0_n , w^1_n,\\cdots w^n - 1_n\$ 即为我们要带入的\$x_0 , x_1 , \\cdots ,x_n\$

\\[w_n^k = cos\\dfrackn2\\pi+isin\\dfrackn2\\pi \\]

单位根的一些性质

1、对任何整数 \$n > 0 , k > 0 , d > 0\$ ，有\$w_dn^dk = w_n^k\$

2、如果 \$n\\ mod \\ 2 == 0\$ ：\$w_n^k+\\fracn2 = -w_n^k\$

它们表示的点关于原点对称，所表示的复数实部相反，所表示的向量等大反向

3、\$w_n^0 = w_n^n\$

FFT

然后用分治来搞 \$DFT\$

设：

\\[A(x) = \\sum_i = 0^n - 1a_ix^i = a_0 +a_1x+\\cdots +a_n-1x^n - 1 \\]

按照 \$A(x)\$ 下标的 奇偶性 分成两半，右边提出一个 \$x\$

\\[A(x) = (a_0+a_2x^2+\\cdots+a_n - 2x^n - 2)+(a_1x+a_3x^3+\\cdots+a_n - 1x^n - 1) \\newline =(a_0+a_2x^2+\\cdots+a_n - 2x^n - 2)+x(a_1+a_3x^2+\\cdots+a_n - 1x^n -2) \\]

令：

\\[A_1(x) = a_0 + a_2x + a_4x^2+\\cdots +a_n - 2x^\\fracn2 - 1\\newline A_2(x) = a_1 + a_3x+a_5x^2+\\cdots+a_n - 1x^\\fracn2-1 \\]

所以：

\\[A(x) = A_1(x^2) + xA_2(x^2) \\]

设 \$k<\\fracn2\$ ，把 \$w_n^k\$ 带入 \$A(x)\$ 得：

\\[A(w_n^k) = A_1((w_n^k)^2) + w_n^kA_2((w_\\fracn2^k))\\newline =A_1(w_n^2k) + w_n^kA_2(w_n2k) = A_1(w_\\fracn2^k) + w_n^kA_2(w_\\fracn2^k) \\]

带入 \$w_n^k+\\fracn2\$

\\[A(w_n^k+\\fracn2) = A_1(w_n^2k+n) + w_n^k+\\fracn2A_2(w_n^2k+n)\\newline = A_1(w_n^2k) - w_n^kA_2(w_n^2kw_n^n)\\newline =A_1(w_n^2k) - w_k^kA_2(w_n^2k) = A_1(w_\\fracn2^k) - w_n^kA_2(w_\\fracn2^k) \\]

我们发现：\$A(w_n^k)\$ 和 \$A(w_n^k+\\fracn2)\$ 后面的东西只有符号不一样，所以我们可以用分治来搞

还要先把 \$n\$ 补成 \$2\$ 幂才能搞

IFFT

积的多项式的 点值表达式 然后转成 系数表达式 叫做 \$IFFT\$

显然：

一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n nn即为原多项式的每一项系数

递归版的FFT

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define fd(x , y , z) for(int x = y ; x >= z ; x --)
#define LL long long
using namespace std;
const int N = 4e6 + 5;
const double pi = acos (-1.0);
struct node 
    double x , y;
 a[N] , b[N];
int n , m , len = 1 , r[N] , l;
node operator + (node a, node b)  return (node)a.x + b.x , a.y + b.y;
node operator - (node a, node b)  return (node)a.x - b.x , a.y - b.y;
node operator * (node a, node b)  return (node)a.x * b.x - a.y * b.y , a.x * b.y + a.y * b.x;
int read () 
    int val = 0 , fu = 1;
    char ch = getchar ();
    while (ch < \'0\' || ch > \'9\') 
        if (ch == \'-\') fu = -1;
        ch = getchar ();
    
    while (ch >= \'0\' && ch <= \'9\') 
        val = val * 10 + (ch - \'0\');
        ch = getchar ();
    
    return val * fu;

void fft (node *A , int inv) 
    for (int i = 0 ; i < len ; i ++)
        if (i < r[i]) 
            swap (A[i] , A[r[i]]);
    for (int mid = 1 ; mid < len ; mid <<= 1) 
        node wn = (node)cos (1.0 * pi / mid) , inv * sin (1.0 * pi / mid);
        for (int R = mid << 1 , j = 0 ; j < len ; j += R) 
            node w = (node)1 , 0;
            for (int k = 0 ; k < mid ; k ++ , w = w * wn) 
                node x = A[j + k] , y = w * A[j + mid + k];
                A[j + k] = x + y;
                A[j + mid + k] = x - y;
            
        
    

int main () 
    n = read () , m = read ();
    fu (i , 0 , n) a[i].x = read ();
    fu (i , 0 , m) b[i].x = read ();
    while (len <= n + m) len <<= 1 , l ++;
    for (int i = 0 ; i < len ; i ++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    fft (a , 1);
    fft (b , 1);
    fu (i , 0 , len) 
        a[i] = a[i] * b[i];
    fft (a , -1);
    // for (int i = 0 ; i <= n + m ; i ++) cout << a[i].x << " " << a[i].y << "\\n";
    fu (i , 0 , n + m) 
        printf ("%d " , (int)(a[i].x / len + 0.5));
    return 0;

后记

迭代版的我也不会。

这个讲的好

快速傅里叶变换(FFT)详解

本文只讨论FFT在信息学奥赛中的应用

文中内容均为个人理解，如有错误请指出，不胜感激

回到顶部

前言

先解释几个比较容易混淆的缩写吧

DFT：离散傅里叶变换—> $O (n^{2})$

FFT：快速傅里叶变换—> $O (n * \log (n)$

FNTT/NTT：快速傅里叶变换的优化版—>优化常数及误差

FWT：快速沃尔什变换—>利用类似FFT的东西解决一类卷积问题

MTT：毛爷爷的FFT—>非常nb/任意模数

FMT 快速莫比乌斯变化—>感谢stump提供

回到顶部

多项式

系数表示法

设 $A (x)$

则 $A (x) = \sum_{i = 0}^{n} a_{i} * x^{i}$

例如： $A (3) = 2 + 3 * x + x^{2}$

利用这种方法计算多项式乘法复杂度为 $O (n^{2})$

（第一个多项式中每个系数都需要与第二个多项式的每个系数相乘）

点值表示法

将 $n$

则该多项式被这 $n$

其中 $y_{i} = \sum_{j = 0}^{n - 1} a_{j} * x_{i}^{j}$

例如：上面的例子用点值表示法可以为 $(0, 2), (1, 6), (2, 12)$

利用这种方法计算多项式乘法的时间复杂度仍然为 $O (n^{2})$

（选点 $O (n)$

我们可以看到，两种方法的时间复杂度都为 $O (n^{2})$

对于第一种方法，由于每个点的系数都是固定的，想要优化比较困难

对于第二种方法，貌似也没有什么好的优化方法，不过当你看完下面的知识，或许就不这么想了

回到顶部

复数

在介绍复数之前，首先介绍一些可能会用到的东西

向量

同时具有大小和方向的量

在几何中通常用带有箭头的线段表示

圆的弧度制

等于半径长的圆弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度。用弧度作单位来度量角的制度叫做弧度制

公式:

$1^{\circ} = \frac{π}{180} r a d$

$180^{\circ} = π r a d$

平行四边形定则

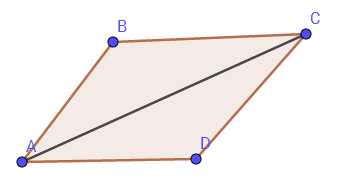
技术分享图片

(好像画的不是很标准。。)

平行四边形定则：AB+AD=AC

复数

定义

设 $a, b$

在复平面中， $x$

模长：从原点 $(0, 0)$

幅角：假设以逆时针为正方向，从 $x$

运算法则

加法：

因为在复平面中，复数可以被表示为向量，因此复数的加法与向量的加法相同，都满足平行四边形定则（就是上面那个）

乘法：

几何定义：复数相乘，模长相乘，幅角相加

代数定义：

(a + b i) ? (c + d i)

= a c + a d i + b c i + b d i 2

= a c + a d i + b c i ? b d

= (a c ? b d) + (b c + a d) i

单位根

下文中，默认 $n$

在复平面上，以原点为圆心， $1$

根据复数乘法的运算法则，其余 $n - 1$

注意 $ω_{n}^{0} = ω_{n}^{n} = 1$

那么如何计算它们的值呢？这个问题可以由欧拉公式解决

ω k n = cos k ? 2 π n + i sin k ? 2 π n

例如

技术分享图片

图中向量 $A B$

单位根的幅角为周角的 $\frac{1}{n}$

在代数中，若 $z^{n} = 1$

单位根的性质

$ω_{n}^{k} = \cos k \frac{2 π}{n} + i \sin k \frac{2 π}{n}$

$ω_{2 n}^{2 k} = ω_{n}^{k}$

证明：

ω 2 k 2 n = cos 2 k ? 2 π 2 n + i sin 2 k ? 2 π 2 n

= ω k n

$ω_{n}^{k + \frac{n}{2}} = - ω_{n}^{k}$

ω n 2 n = cos n 2 ? 2 π n + i sin n 2 ? 2 π n

= cos π + i sin π

= ? 1

$ω_{n}^{0} = ω_{n}^{n} = 1$

讲了这么多，貌似跟我们的正题没啥关系啊。。

OK！各位坐稳了，前方高能！

回到顶部

快速傅里叶变换

我们前面提到过，一个 $n$

那么我们可以把单位根的 $0$

我们设多项式 $A (x)$

那么

A (x) = a 0 + a 1 ? x + a 2 ? x 2 + a 3 ? x 3 + a 4 ? x 4 + a

将其下标按照奇偶性分类

A (x) = (a 0 + a 2 ? x 2 + a 4 ? x 4 + ? + a n ? 2 ? x n ? 2

设

A 1 (x) = a 0 + a 2 ? x + a 4 ? x 2 + ? + a n ? 2 ? x n 2

A 2 (x) = a 1 + a 3 ? x + a 5 ? x 2 + ? + a n ? 1 ? x n 2

那么不难得到

A (x) = A 1 (x 2) + x A 2 (x 2)

我们将 $ω_{n}^{k} (k < \frac{n}{2})$

A (ω k n) = A 1 (ω 2 k n) + ω k n A 2 (ω 2 k n)

= A 1 (ω k n 2 ) + ω k n A 2 ( ω k n 2 )

同理，将 $ω_{n}^{k + \frac{n}{2}}$

A (ω k + n 2 n ) = A 1 ( ω 2 k + n n ) + ω k + n 2 n ( ω 2

= A 1 (ω 2 k n ? ω n n) ? ω k n A 2 (ω 2 k n ? ω n n)

= A 1 (ω 2 k n) ? ω k n A 2 (ω 2 k n)

大家有没有发现什么规律？

没错！这两个式子只有一个常数项不同！

那么当我们在枚举第一个式子的时候，我们可以 $O (1)$

又因为第一个式子的 $k$

所以我们将原来的问题缩小了一半！

而缩小后的问题仍然满足原问题的性质，所以我们可以递归的去搞这件事情！

直到多项式仅剩一个常数项，这时候我们直接返回就好啦

时间复杂度：

不难看出FFT是类似于线段树一样的分治算法。

因此它的时间复杂度为 $O (n l o g n)$

回到顶部

快速傅里叶逆变换

不要以为FFT到这里就结束了。

我们上面的讨论是基于点值表示法的。

但是在平常的学习和研究中很少用点值表示法来表示一个多项式。

所以我们要考虑如何把点值表示法转换为系数表示法，这个过程叫做傅里叶逆变换

$(y_{0}, y_{1}, y_{2}, \dots, y_{n - 1})$

设有另一个向量 $(c_{0}, c_{1}, c_{2}, \dots, c_{n - 1})$

c k = \sum i = 0 n ? 1 y i (ω ? k n) i

即多项式 $B (x) = y_{0}, y_{1} x, y_{2} x^{2}, \dots, y_{n - 1} x^{n - 1}$

emmmm又到推公式时间啦

$(c_{0}, c_{1}, c_{2}, \dots, c_{n - 1})$

c k = \sum i = 0 n ? 1 y i (ω ? k n) i

= \sum i = 0 n ? 1 (\sum j = 0 n ? 1 a j (ω i n) j) (ω ? k n

= \sum i = 0 n ? 1 (\sum j = 0 n ? 1 a j (ω j n) i) (ω ? k n

= \sum i = 0 n ? 1 (\sum j = 0 n ? 1 a j (ω j n) i (ω ? k n)

= \sum i = 0 n ? 1 \sum j = 0 n ? 1 a j (ω j n) i (ω ? k n) i

= \sum i = 0 n ? 1 \sum j = 0 n ? 1 a j (ω j ? k n) i

= \sum j = 0 n ? 1 a j (\sum i = 0 n ? 1 (ω j ? k n) i)

设 $S (x) = \sum_{i = 0}^{n - 1} x^{i}$

将 $ω_{n}^{k}$

S (ω k n) = 1 + (ω k n) + (ω k n) 2 + \dots (ω k n) n ? 1

当 $k! = 0$

等式两边同乘 $ω_{n}^{k}$

ω k n S (ω k n) = ω k n + (ω k n) 2 + (ω k n) 3 + \dots (ω k n) n

两式相减得

ω k n S (ω k n) ? S (ω k n) = (ω k n) n ? 1

S (ω k n) = ( ω k n ) n ? 1 ω k n ? 1

S (ω k n) = ( ω n n ) k ? 1 ω k n ? 1

S (ω k n) = 1 ? 1 ω k n ? 1

观察这个式子，不难看出它分母不为0，但是分子为0

因此，当 $K! = 0$

那当 $k = 0$

很显然， $S (ω_{n}^{0}) = n$

继续考虑刚刚的式子

c k = \sum j = 0 n ? 1 a j (\sum i = 0 n ? 1 (ω j ? k n) i)

当

j \neq k

c k = n a k

j \neq k

a k = c k n

这样我们就得到点值与系数之间的表示啦

回到顶部

理论总结

至此，FFT的基础理论部分就结束了。

我们来小结一下FFT是怎么成功实现的

首先，人们在用系数表示法研究多项式的时候遇阻

于是开始考虑能否用点值表示法优化这个东西。

然后根据复数的两条性质（这个思维跨度比较大）得到了一种分治算法。

最后又推了一波公式，找到了点值表示法与系数表示法之间转换关系。

emmmm

其实FFT的实现思路大概就是

系数表示法—>点值表示法—>系数表示法

引用一下远航之曲大佬的图

技术分享图片

当然，再实现的过程中还有很多技巧

我们根据代码来理解一下

回到顶部

递归实现

递归实现的方法比较简单。

就是按找我们上面说的过程，不断把要求的序列分成两部分，再进行合并

在c++的STL中提供了现成的complex类，但是我不建议大家用，毕竟手写也就那么几行，而且万一某个毒瘤卡STL那岂不是很ＧＧ？

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int MAXN=2*1e6+10;
inline int read()
{
    char c=getchar();int x=0,f=1;
    while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();}
    while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();}
    return x*f;
}
const double Pi=acos(-1.0);
struct complex
{
    double x,y;
    complex (double xx=0,double yy=0){x=xx,y=yy;}
}a[MAXN],b[MAXN];
complex operator + (complex a,complex b){ return complex(a.x+b.x , a.y+b.y);}
complex operator - (complex a,complex b){ return complex(a.x-b.x , a.y-b.y);}
complex operator * (complex a,complex b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看复数的运算那部分 
void fast_fast_tle(int limit,complex *a,int type)
{
    if(limit==1) return ;//只有一个常数项
    complex a1[limit>>1],a2[limit>>1];
    for(int i=0;i<=limit;i+=2)//根据下标的奇偶性分类
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fast_fast_tle(limit>>1,a1,type);
    fast_fast_tle(limit>>1,a2,type);
    complex Wn=complex(cos(2.0*Pi/limit) , type*sin(2.0*Pi/limit)),w=complex(1,0);
    //Wn为单位根，w表示幂
    for(int i=0;i<(limit>>1);i++,w=w*Wn)//这里的w相当于公式中的k 
        a[i]=a1[i]+w*a2[i],
        a[i+(limit>>1)]=a1[i]-w*a2[i];//利用单位根的性质，O(1)得到另一部分 
}
int main()
{
    int N=read(),M=read();
    for(int i=0;i<=N;i++) a[i].x=read();for(int i=0;i<=M;i++) b[i].x=read();int limit=1;while(limit<=N+M) limit<<=1;
    fast_fast_tle(limit,a,1);
    fast_fast_tle(limit,b,1);//后面的1表示要进行的变换是什么类型//1表示从系数变为点值//-1表示从点值变为系数 //至于为什么这样是对的，可以参考一下c向量的推导过程， for(int i=0;i<=limit;i++)
        a[i]=a[i]*b[i];
    fast_fast_tle(limit,a,-1);for(int i=0;i<=N+M;i++) printf("%d ",(int)(a[i].x/limit+0.5));//按照我们推倒的公式，这里还要除以n return0;}

这里还有一个听起来很装B的优化—蝴蝶操作

观察合并的过程，w*a2[i] 这一项计算了两次，因为理论上来说复数的乘法是比较慢的，所以我们可以把这一项记出来

    for(int i=0;i<(limit>>1);i++,w=w*Wn)//这里的w相当于公式中的k 
    {
        complex t=w*a2[i];//蝴蝶操作
        a[i]=a1[i]+t,
        a[i+(limit>>1)]=a1[i]-t;//利用单位根的性质，O(1)得到另一部分     
    }

技术分享图片

woc? 脸好疼。。。。。。

咳咳。

速度什么的才不是关键呢？

关键是我们AC不了啊啊啊

表着急，AC不了不代表咱们的算法不对，只能说这种实现方法太low了

下面介绍一种更高效的方法

回到顶部

迭代实现

再盗一下那位大佬的图

技术分享图片

观察一下原序列和反转后的序列？

聪明的你有没有看出什么显而易见的性质？

没错！

我们需要求的序列实际是原序列下标的二进制反转！

因此我们对序列按照下标的奇偶性分类的过程其实是没有必要的

这样我们可以 $O (n)$

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int MAXN=1e7+10;
inline int read()
{
    char c=getchar();int x=0,f=1;
    while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();}
    while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();}
    return x*f;
}
const double Pi=acos(-1.0);
struct complex
{
    double x,y;
    complex (double xx=0,double yy=0){x=xx,y=yy;}
}a[MAXN],b[MAXN];
complex operator + (complex a,complex b){ return complex(a.x+b.x , a.y+b.y);}
complex operator - (complex a,complex b){ return complex(a.x-b.x , a.y-b.y);}
complex operator * (complex a,complex b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看复数的运算那部分 
int N,M;
int l,r[MAXN];
int limit=1;
void fast_fast_tle(complex *A,int type)
{
    for(int i=0;i<limit;i++) 
        if(i<r[i]) swap(A[i],A[r[i]]);//求出要迭代的序列 
    for(int mid=1;mid<limit;mid<<=1)//待合并区间的中点
    {
        complex Wn( cos(Pi/mid) , type*sin(Pi/mid) ); //单位根 
        for(int R=mid<<1,j=0;j<limit;j+=R)//R是区间的右端点，j表示前已经到哪个位置了 
        {
            complex w(1,0);//幂 
            for(int k=0;k<mid;k++,w=w*Wn)//枚举左半部分 
            {
                 complex x=A[j+k],y=w*A[j+mid+k];//蝴蝶效应 
                A[j+k]=x+y;
                A[j+mid+k]=x-y;}}}}int main(){int N=read(),M=read();for(int i=0;i<=N;i++) a[i].x=read();for(int i=0;i<=M;i++) b[i].x=read();while(limit<=N+M) limit<<=1,l++;for(int i=0;i<limit;i++)
        r[i]=( r[i>>1]>>1)|((i&1)<<(l-1));// 在原序列中 i 与 i/2 的关系是 ： i可以看做是i/2的二进制上的每一位左移一位得来// 那么在反转后的数组中就需要右移一位，同时特殊处理一下奇数 
    fast_fast_tle(a,1);
    fast_fast_tle(b,1);for(int i=0;i<=limit;i++) a[i]=a[i]*b[i];
    fast_fast_tle(a,-1);for(int i=0;i<=N+M;i++)
        printf("%d ",(int)(a[i].x/limit+0.5));return0;}

以上是关于FFT（快速傅里叶变换）的主要内容，如果未能解决你的问题，请参考以下文章

快速傅里叶变换FFT及其延伸（只是一个引导）