Description

Solution
考虑犯错误的条件:之前是处于必胜状态,该操作之后就变成了必败状态.
我们可以把这个过程看成两人对网格图进行黑白染色,变成了一个二分图模型,即当前位置向相邻不同颜色的位置连边,构成的二分图,一次游戏相当于一个最大匹配.
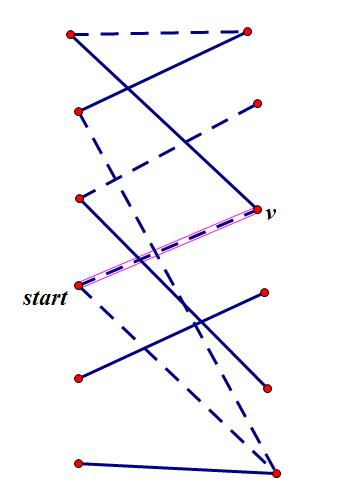
一个结论:如果一定存在包含当前位置的最大匹配,那么处于先手必胜状态
证明:
因为当前点不处于最大匹配中,那么只有非匹配边可以走,假设走到了\\(v\\),\\(v\\)点则可以走匹配边,假设走了一条匹配边,则到达的下一个点只能走非匹配边,因为匹配的点是\\(v\\), 综上:先手只能一直沿着非匹配边走,而后手有匹配边可以走,所以不是必胜状态
所以只需要判断一个点是否在一定在最大匹配中了
方法是:删除该点,再跑一次最大匹配,如果能成功匹配则不满足条件.
一个细节:一定不会存在回路,即一个点只会走一次,所以走过的点不能再进入匹配中
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#define RG register
#define il inline
#define iter iterator
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
using namespace std;
typedef long long ll;
const int N=45;
int x,y,nxt[N*N*8],to[N*N*8],num=0,w[N*N];
int n,m,a[N][N],id[N][N],cnt=0;char s[N];
bool vis[N*N],ans[N*N*2];int b[N*N],head[N*N];
void link(int x,int y){nxt[++num]=head[x];to[num]=y;head[x]=num;}
inline bool dfs(int x){
for(int i=head[x];i;i=nxt[i]){
int u=to[i];
if(!vis[u] && !w[u]){
vis[u]=1;
if(!b[u] || dfs(b[u])){
b[u]=x;b[x]=u;
return true;
}
}
}
return false;
}
void build(){
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(((i+j)&1)^((x+y)&1)^(a[i][j]==1))
id[i][j]=++cnt;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(!id[i][j])continue;
if(i<n && id[i+1][j])link(id[i][j],id[i+1][j]);
if(i>1 && id[i-1][j])link(id[i][j],id[i-1][j]);
if(j<m && id[i][j+1])link(id[i][j],id[i][j+1]);
if(j>1 && id[i][j-1])link(id[i][j],id[i][j-1]);
}
}
void work()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%s",s+1);
for(int j=1;j<=m;j++){
if(s[j]==\'X\')a[i][j]=1;
else if(s[j]==\'O\')a[i][j]=2;
else x=i,y=j,a[i][j]=1;
}
}
build();
for(int i=1;i<=cnt;i++){
if(!b[i]){
memset(vis,0,sizeof(vis));
dfs(i);
}
}
int Q,ret=0;
cin>>Q;
for(int i=1;i<=Q<<1;i++){
w[id[x][y]]=1;
if(!b[id[x][y]])ans[i]=0;
else{
int u=id[x][y],v=b[u];
b[u]=b[v]=0;
memset(vis,0,sizeof(vis));
ans[i]=(!dfs(v));
}
scanf("%d%d",&x,&y);
}
for(int i=1;i<=Q;i++)
if(ans[2*i-1]&ans[i<<1])ret++;
printf("%d\\n",ret);
for(int i=1;i<=Q;i++)
if(ans[2*i-1]&ans[i<<1])printf("%d\\n",i);
}
int main()
{
freopen("pp.in","r",stdin);
freopen("pp.out","w",stdout);
work();
return 0;
}