费马小定理&欧拉定理

Posted 2020-06-09

在p是素数的情况下，对任意整数x都有x^p≡x(mod p)。这个定理被称作费马小定理其中如果x无法被p整除，我们有x^p-1≡1(mod p)。利用这条性质，在p是素数的情况下，就很容易求出一个数的逆元。那上面的式子变形之后得到a^-1≡a^p-2(mod p)，因此可以通过快速幂求出逆元。

我们先来证明一下费马小定理：

费马小定理证明：

 

一、准备知识

 

引理1：剩余系定理2

 

若a,b,c为任意3个整数,m为正整数,且(m,c)=1,则当ac≡bc(mod m)时,有a≡b(mod m)
证明：ac≡bc(mod m)可得ac–bc≡0(mod m)可得(a-b)c≡0(mod m)因为(m,c)=1即m,c互质,c可以约去,a–b≡0(mod m)可得a≡b(mod m)

 

引理2：剩余系定理5

 

若m为整数且m>1,a[1],a[2],a[3],a[4],…a[m]为m个整数,若在这m个数中任取2个整数对m不同余,则这m个整数对m构成完全剩余系.
证明：构造m的完全剩余系（0,1,2,…m-1）,所有的整数必然这些整数中的1个对模m同余.取r[1]=0,r[2]=1,r[3]=2,r[4]=3,…r=i-1,1<i<=m.令(1)：a[1]≡r[1](mod m)(顺序可以不同),因为只有在这种情况下才能保证集合{a1,a2,a3,a4,…am}中的任意2个数不同余,否则必然有2个数同余.由式(1)自然得到集合{a1,a2,a3,a4,…am}对m构成完全剩余系.

 

引理3：剩余系定理7
设m是一个整数,且m>1,b是一个整数且(m,b)=1.如果a1,a2,a3…am是模m的一个完全剩余系,则ba[1],ba[2],ba[3],ba[4],…ba[m]也构成模m的一个完全剩余系.
证明：若存在2个整数ba和ba[j]同余即ba≡ba[j](mod m),根据引理2则有a≡a[j](mod m).根据完全剩余系的定义和引理4（完全剩余系中任意2个数之间不同余,易证明）可知这是不可能的,因此不存在2个整数ba和ba[j]同余.由引理5可知ba[1],ba[2],ba[3],ba[4],…ba[m]构成模m的一个完全剩余系.

 

引理4：同余定理6
如果a,b,c,d是四个整数,且a≡b(mod m),c≡d(mod m),则有ac≡bd(mod m)
证明：由题设得ac≡bc(mod m),bc≡bd(mod m),由模运算的传递性可得ac≡bc(mod m)

 

二、证明过程：
构造素数p的完全剩余系P={1,2,3,4…(p-1)},因为(a, p)=1,由引理3可得A={a,2a,3a,4a,…(p-1)a}也是p的一个完全剩余系.令W=1*2*3*4…*(p-1),显然W≡W(mod p).令Y=a*2a*3a*4a*…(p-1)a,因为{a,2a,3a,4a,…(p-1)a}是p的完全剩余系,由引理2以及引理4可得a*2a*3a*…(p-1)a≡1*2*3*…(p-1)(mod p)即W*a^(p-1)≡W(modp).易知(W,p)=1,由引理1可知a^(p-1)≡1(mod p）

 

补充：在p不是素数的情况下，我们也有类似的欧拉定理可以使用。欧拉函数是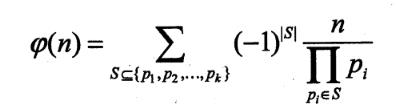然后再有欧拉定理我们就可以得到乘法逆元。

 

欧拉定理：

 

一、准备知识：

 

欧拉函数：在数论中，对于正整数n，欧拉函数是小于n的数与n互质的数的数目。Φ(m)=m×П(p_i-1)/p_i

 

证明：先给出任意的正整数n=p₁^a[1]*p₂^a[2]*……*p_k^a[k]

 

然后用容斥原理，首先从总数n中减去n/p₁，n/p₂,……n/p_k的个数然后再加上同时是两个素因子的倍数的个数，再减去同时是三个素因子的倍数的个数……这样我们就可以得到一个公式：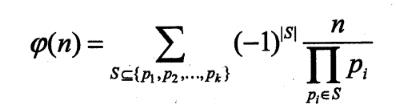

 

 

 

现在有了公式，可是这个公式的时间复杂度是O(2^k),所以我们需要对其进行化简，这步并不简单，但最后可以化简出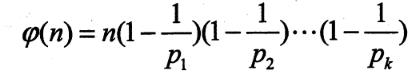         

 

二、证明

 

a^φ(n) * x₁ * x₂ *... * x_φ(n) mod n ≡ (a * x₁) * (a * x₂) * ... * (a * x_φ(n)) mod n

 

≡ (a * x₁ mod n) * (a * x₂ mod n) * ... * (a * x_φ(n) mod n) mod n
≡  x₁ * x₂ * ... * x_φ(n) mod n
对比等式的左右两端，因为x_i  (1 ≤ i ≤ φ(n)) 与 n 互质，所以 a^φ(n) ≡  1 (mod n)