这里主要是贴出我个人实现的代码
做出以下测试说明
1 分类并不能百分百正确,可能存在一些点无法正确分类的情况
2 由于没有引入代价函数,也没有使用梯度算法,这个学习率并不是非常准确,分离超平面可能不正确。同样的参数下,可以多运行几次,会出现正确的结果的。
3 希望感兴趣的朋友可以去实验以下,调整双月间距,多做几次实验。
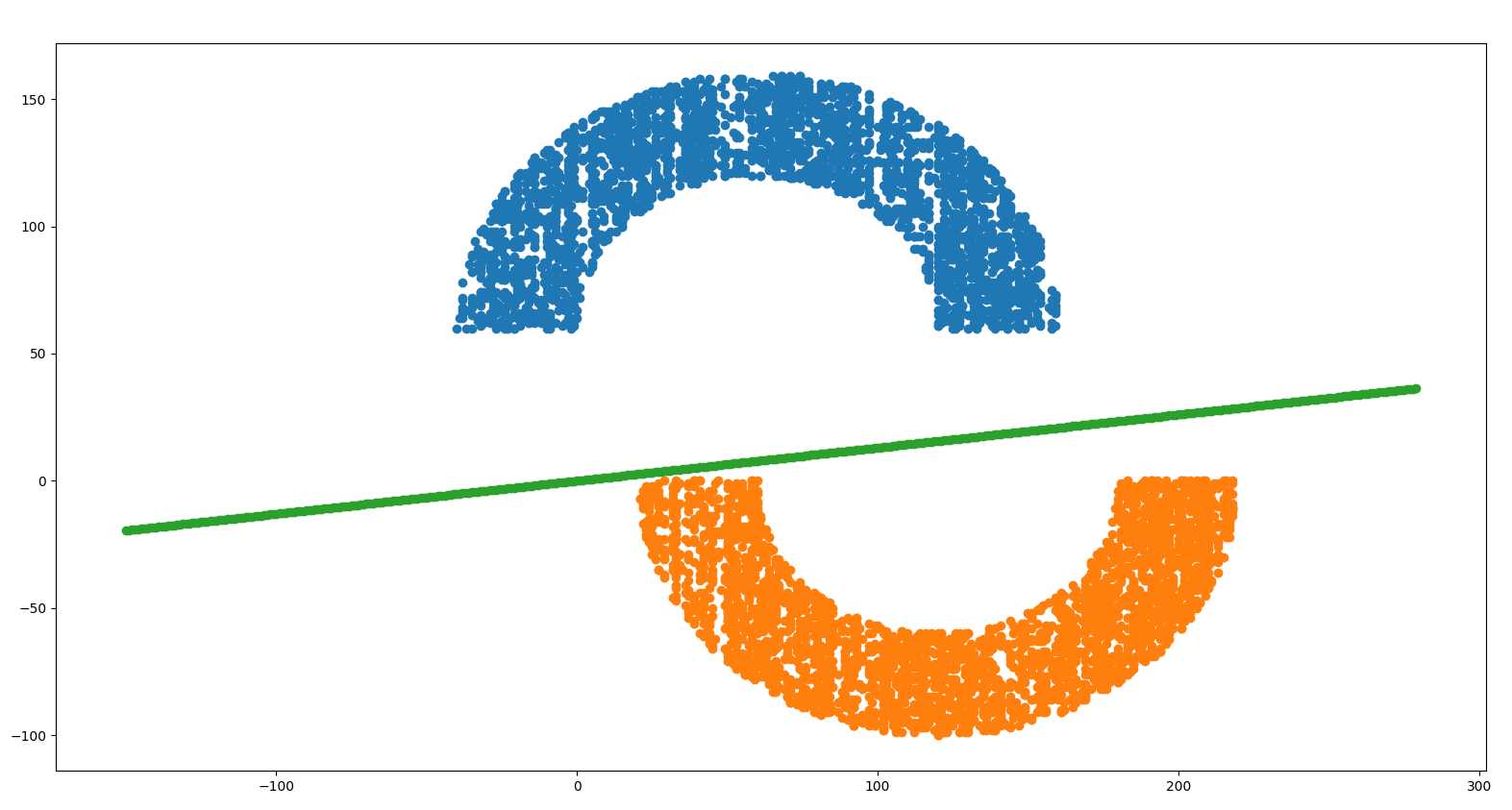
这个算法主要验证了感知器算法是可以收敛的,并不保证能百分百分类正确!原因在前文也说明了。
希望大家能和我一起思考:如果改变数据的迭代方式(训练数据集)会对分类效果造成什么影响,为什么会有这些影响,如何消除?
#!/usr/bin/env python # -*- coding:utf-8 -*- import random import matplotlib.pyplot as plt import numpy as np import math # 生成上部的半月 def gernarateUp(radius,center,alf): xsiy = [] ysiy= [] for x in range(center[0]-radius,center[0]+radius,1): counts = random.randint(0, alf*radius) for y in range(counts): r= random.randint(center[1], center[1] + radius) if np.sqrt((x-center[0])**2+(r-center[1])**2)>=alf*radius and np.sqrt((x-center[0])**2+(r-center[1])**2)<=radius: xsiy.append(x) ysiy.append(r) return [xsiy,ysiy] #生成下部的半月 def gernaratefloor(radius,center,alf): xsiy = [] ysiy= [] for x in range(center[0]-radius,center[0]+radius,1): counts = random.randint(0, alf*radius) for y in range(counts): r= random.randint(center[1] - radius,center[1]) if np.sqrt((x-center[0])**2+(r-center[1])**2)>=alf*radius and np.sqrt((x-center[0])**2+(r-center[1])**2)<=radius: xsiy.append(x) ysiy.append(r) return [xsiy,ysiy] #生成双半月 # radius -- 半径 # center -- 上月圆心位置 # akf -- 内径比例 # x -- 下月圆心与上月圆心 在x轴上的距离 大于零时 往右移动 #y --- 下月圆心与上月圆心 在y 轴上的距离 大于零时 往上移动 def gernarate(radius,center,alf,x,y): floorCenter=[center[0]+x,center[1]+y] upCenter=center upSet = gernarateUp(radius,upCenter,alf) floorSet = gernaratefloor(radius,floorCenter,alf) return upSet,floorSet # 感知器模型实现 def perceptron(w,x): # 线性计算部分 z = np.sum(np.dot(w,x)) # 激活函数部分 if z>0: return 1 if z<=0: return -1 # 学习率计算 def learningRate(w,x): z = np.sum(np.dot(w, x)) xx = np.sum(np.dot(x, x)) r = math.ceil(abs(z) / xx) + 1 return r # 针对每个输入的权值更新操作 def wRefresh(w,x,d): a=0 flag =True while flag: a=a+1 y=perceptron(w,x) r=learningRate(w,x) w = w + r * (d - y) * x if (d - y)==0: flag=False return w if __name__ == ‘__main__‘: # 初始化 上下半月 upSet, floorSet = gernarate(100,[60,60],0.6,60,-60) #初始化权值向量 # 数据点的输入是二维的,第一个参数为偏置,第二参数为点的x坐标的权值,第三个参数为点的y坐标的权值 # 这样处理的原因是我们后续的计算中将使用 感知器的简写形式来计算 w = np.array([0,0,0]) # 初始化输入向量 # 上半月的数据长度 upx =upSet[0] # 初始化1list bx = [] for x in upSet[0]: bx.append(1) # 整合输入,将二维输入调整为3维度输入 # [x,y]的形式变化为[1,x,y] upy= upSet[1] upInput = [] upInput.append(bx) upInput.append(upx) upInput.append(upy) # 将数据转化为numpy类 upInput = np.array(upInput).T # 同上,整合输入数据,这里只不过是针对下月做处理 ax = [] for x in floorSet[0]: ax.append(1) floorInput = [] floorInput.append(ax) floorInput.append(floorSet[0]) floorInput.append(floorSet[1]) floorInput = np.array(floorInput).T # 由于上月与下月的数据点的数量不一定一致,这里做一个边缘处理 # 获取数据长度较小的那个 长度 min = min(upInput.shape[0],floorInput.shape[0]) # 逐行迭代 # 这里要说明一点,以下采用了上月和下月数据交替运算的方式。 for x in range(min): w = wRefresh(w, upInput[x,], 1) w = wRefresh(w, floorInput[x,], -1) # 对多出来的部分做处理 temp=None tempD=None if upInput.shape[0]>floorInput.shape[0]: temp=upInput tempD=1 else: temp=floorInput tempD=-1 #由于数据长度较短的 那个半月已经迭代完毕,这里对剩余的数据进行迭代 for x in range(min,max((upInput.shape[0],floorInput.shape[0]))): w = wRefresh(w, temp[x,], tempD) # 下面是分开迭代的方法,大家可以试一试,这样可能会出现无法正确分类的情况,思考下为什么! # for x in upInput: # w = wRefresh(w,x,1) # print w # for x in floorInput: # w = wRefresh(w,x,-1) # 数据描点(双月数据描点) plt.scatter(upSet[0], upSet[1]) plt.scatter(floorSet[0], floorSet[1]) # 超平面绘制 # 0 = w[1]x+w[2]y+w[0] 由此式子活得y与x的关系 xxxi=[] yyyyi=[] for x in range(-150,280): xxxi.append(x) yyyyi.append(x*(-w[1]/w[2])+w[0]/w[2]) # 数据描点(超平面描点) plt.scatter(xxxi, yyyyi) #数据展示 plt.show()