判断无向图是否有回路（是否有环）

Posted 2020-10-17

总体思路：

（1）通过广度遍历（BFS）访问图的所有点，对于每个点，都检测和已访问过的点是否有边（除了和它连接的上层节点）。

（1.1）如果有边，说明有回路（有环）。如果对于每个点，都没有和已访问过的点有边，说明从该点出发的当前图没有回路（无环）。

（2）如果从任意点开始的BFS，以上操作（1）均说明无回路，则没有回路。

适用范围：

（1）判断图添加一条无向边后是否有回路。只要从这条新边的一个点出发执行操作（1）即可。

（2）判断一个图是否有回路。需要从任意点都执行一次操作（1），只有所有操作（1）均说明无回路，才表明没有回路。

举个例子：

假如有下面的一个图：

 

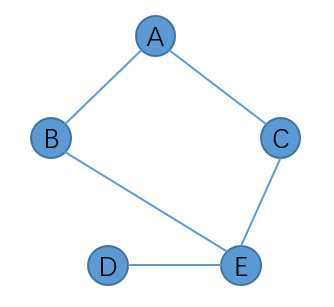
那么，假如从A点出发开始BFS

（1）那么就是A先被访问，然后通过A可以访问到B、C。

（2）当访问B时，此时只有A已访问，按照规则，需要判断B和其他已访问节点是否有边（除了和它连接的上层节点A）。此时已访问节点除了A，无其他已访问节点。那么继续下一个点。。

（3）当访问C时，此时A、B都已访问，按照规则，需要判断B和其他已访问节点是否有边（除了和它连接的上层节点A）：此时已访问节点除了A，还有B。故判断B/C之间是否有边，结果是无边。那么继续下一个点。

（4）通过B，无其他节点可以访问。

（5）通过C，可以访问到E。

（6）当访问E时，此时A、B、C都已访问，按照规则，需要判断B和其他已访问节点是否有边（除了和它连接的上层节点C）：此时已访问节点除了C，还有A、B。故判断A/E、B/E之间是否有边，结果是B/E有边，说明有回路，终止循环。

本文博客地址：http://www.cnblogs.com/toulanboy/

 代码实现

 1     //从某点出判断无向图是否有回路（图用邻接矩阵表示）。假如有N个点，需要调用N次该函数。因为考虑到孤立点的因素，需要从每个点都开始一次。
 2     bool isHuiLu(int begin, int temp[][MAXLEN])
 3     {
 4         bool flag[MAXLEN];
 5         int i, j;
 6         stack <int>stk;
 7         queue <int> vexQueue;
 8         for (i = 0; i<vexnum; i++)
 9             flag[i] = false;
10         //从a或b点出发，广度遍历所有点
11         //如果该点和之前已访问过的点（除了它父亲）有边，
12         //说明有回路
13         vexqueue.push(begin);
14         flag[begin] = true;
15         int father;
16         while (vexqueue.empty() == false) {
17             father = vexQueue.front();
18             vexQueue.pop();
19             for (int i = 0; i < vexnum; ++i) {
20                 if (temp[father][i] != MAX && flag[i] == false) {
21                     vexQueue.push(i);
22                     flag[i] = true;
23                     //看看当前点和其他已访问点是否有边
24                     for (int j = 0; j < vexnum; ++j) {
25                         if (temp[i][j] != MAX && j != father && flag[j] == true) {
26                             return true;//如果有边，说明有回路
27                         }
28                     }
29 
30                 }
31 
32             }
33         }
34         return false;    
35     }

 

 

本文博客地址：http://www.cnblogs.com/toulanboy/